Теплопроводность
Общие положения. Перенос теплоты за счет теплопроводности зависит от распределения температуры по объему тела. Совокупность значений температуры во всех точках тела в данный момент времени называется температурным полем. Математическое выражение температурного поля связывает температуру t с пространственными координатами любой точки х, у, z в данный момент времени t:
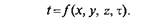
Если температура является функцией одних только пространственных координат (х, у, z), то такое поле называется стационарным, или установившимся. Однако часто температура каждой точки тела зависит также от времени t, т.е. t =f(x, у, z, t), и тогда поле называется нестационарным, или неустановившимся. Так, например, нагревающаяся в печи стальная заготовка имеет нестационарное поле, а в прогревшейся стенке здания температура каждой точки не меняется во времени и ее температурное поле будет стационарным.
Очевидно, что для установившегося теплового режима
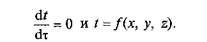
Поверхность, объединяющую точки равной температуры, называют изотермической.
По закону Фурье (3.1)
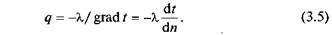
Коэффициент теплопроводности
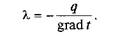
Знак минус в уравнении (3.1) указывает на то, что вектор q направлен противоположно вектору grad t, т.е. в сторону наибольшего уменьшения температуры (рис. 3.1).
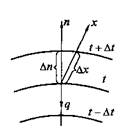
Рис.3.1. К пояснению закона теплопроводности Фурье
Отсюда видно, что коэффициент теплопроводности представляет собой количество теплоты, переносимой в единицу времени через единицу поверхности материала при падении температуры на один градус на единицу длины.
Опытным путем установлено, что коэффициент теплопроводности зависит от свойств вещества (его плотности, структуры, влажности и т.п.) и параметров состояния (давления, температуры). Значения l для различных веществ и условий сводятся в таблицы (табл. 3.1). В ответственных случаях для специфических условий их определяют непосредственно в лаборатории. Зависимость lот температуры для большинства материалов имеет линейный характер.
Таблица 3.1. Коэффициенты теплопроводности
| Вещество | t, °С | X, Вт/(м-К) |
| Металлы: | — | "~~~^^^Ш~~\ |
| Серебро | ||
| Медь | ||
| Алюминий | ||
| Сталь | 50,1 | |
| Ртуть | 8,2 | |
| Строительные и изоляционные материалы: | —■ | 0,023...2,9 |
| Кирпич шамотный | 0,75 | |
| Кирпич красный | 0,6...0,66 | |
| Песок (влажность 10%) | '0...40 | 0,57.. .0,83 |
| Стеклянная вата (влажность 10%) | 20...30 | 0,052 |
| Асбест | 0,072 | |
| Котельная накипь | 0,08...2,3 | |
| Ламповая сажа | 0,07...0,116 | |
| Вода | 0/100 | 0,55/0,68 |
| Воздух | 0/100 | 0,0244/0,0805 |
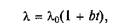
где l0 — значение l при 0 °С; b — постоянная, зависящая от свойств материала.
Однако в технических расчетах значения l принимаются обычно постоянными, равными среднеарифметическим в данных пределах изменения температуры.
Для решения задачи по определению количества теплоты, передаваемой теплопроводностью, было найдено дифференциальное уравнение теплопроводности при следующих допущениях: тело однородно, изотропно, физические параметры его постоянны.
Общее дифференциальное уравнение теплопроводности в декартовой системе координат:
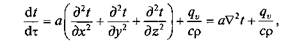
где dt/dt — скорость изменения температуры; α =l/cr – коэффициент температуропроводности, величина которого пропорциональна скорости прогрева (или остывания), м2/с; qv — удельная объемная теплопроизводительность внутренних источников, Вт/м3; Ñ2t — дифференциальный оператор Лапласа.
Наиболее простые соотношения получаются при условии стационарного (установившегося) режима, в которых температура тела не зависит от времени, т.е. dt/dt = 0, следовательно,
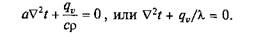
При отсутствии внутренних источников тепла для одномерной задачи получим
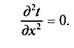
Теплопроводность плоской стенки. Из предыдущего следует, что для плоской стенки, или иначе для неограниченной пластины, условие установившегося режима выражается уравнением
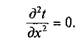
Решив это уравнение, получим dt/dx = с1, и, следовательно,

где c1 и с2 - постоянные интегрирования.
Отсюда вытекает, что в плоской стенке без внутренних источников теплоты температура распределяется по закону прямой линии (рис. 3.2, а).
Определив значения постоянных (приняв один раз х = 0, а другой раз х = d) и подставив их в уравнение (3.6), найдем значение температуры в любой точке:
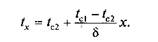
Тепловой поток, проходящий через 1 м2 стенки, можно выразить следующим образом:
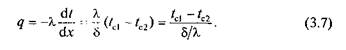
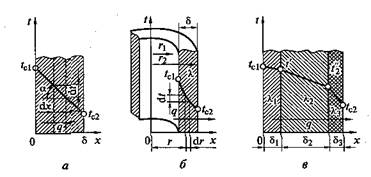
Рис. 3.2. Теплопроводность через плоскую (а),цилиндрическую (б)и многослойную (в)стенки
Закон Фурье можно записать в форме, аналогичной закону Ома в электротехнике, введя понятие о тепловом (термическом) сопротивлении:
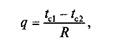
где 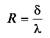 — тепловое (термическое) сопротивление стенки, м2×К/Вт.
— тепловое (термическое) сопротивление стенки, м2×К/Вт.
Для многослойной сложной стенки, состоящей из п слоев, тепловое сопротивление будет равно сумме сопротивлений отдельных слоев:
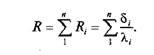
В этом случае удельный тепловой поток может быть определен по формуле
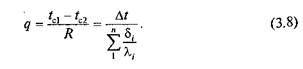
Распределение температур внутри многослойной стенки изображается ломаной линией (рис. 3.2, в).
Теплопроводность цилиндрической стенки трубы.Цилиндрические стенки встречаются очень часто в различных трубопроводах, в поверхностях нагрева всевозможных теплообменных аппаратов, котельных агрегатах и т.д. Требуется рассчитать тепловой поток, передаваемый через цилиндрическую стенку трубы. Задача о распространении теплоты в цилиндрической стенке при известных и постоянных температурах на внутренней и наружной поверхностях также одномерная, если ее рассматривать в цилиндрических координатах. Температура изменяется только вдоль радиуса (по координате r), а по длине трубы и по ее периметру остается неизменной (рис. 3.2, б). В этом случае grad t = dt/drи закон Фурье будет иметь вид
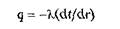
или
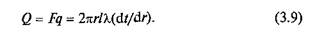
Интегрирование уравнения (3.9) в определенных пределах (по tот tc1 до tc2и по r от r1до r2) дает зависимость для расчета теплового потока Q (Вт) через цилиндрическую стенку:
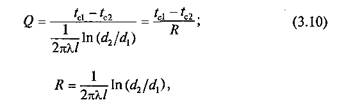
где l и d —- соответственно длина и диаметр трубы, м.
Количество теплоты, отнесенное к 1 м длины трубы, определяется по формуле
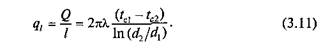
Температура внутри стенки распределяется по логарифмической кривой, изображенной на рис. 3.2, б.
Для многослойной цилиндрической трубы, покрытой п слоями тепловой изоляции, количество теплоты, отнесенное к 1 м длины трубы, определяется по формуле
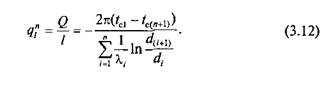
Дата добавления: 2015-10-19; просмотров: 1331;
