Преломление и отражение радиоволн в ионосфере

Для определения условий распространения радиоволн в сферически и электрически неоднородной ионосфере рассмотрим упрощенную, справедливую для сравнительно небольших расстояний (примерно до 1000 км) модель плоскослоистой ионосферы. Будем полагать, что ионосфера состоит из большого числа тонких слоев (рисунок 18).

В каждом слое значение 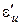, постоянно, величины которых меняются от слоя к слою. Аналогично изменяется и показатель преломления .

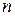Оценим форму траектории радиоволны, распространяющейся в ионосфере. Для выбранной модели ионосферы траектория распространения радиоволны будет определяться законом преломления:

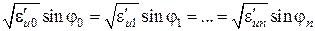
Поскольку распространение волны происходит из оптически более плотной в оптически менее плотную среду, 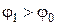, 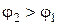и т. д. Для отклонения радиоволны обратно к Земле в верхней точке траектории движения угол 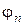должен составлять 90°. Тогда условие отражения запишется в виде:

, ,

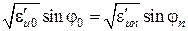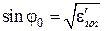так как (граница с тропосферой) и .

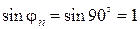Подставляя сюда найденное значение относительной диэлектрической проницаемости ионосферы, получим

.

При уменьшении толщины слоев относительная диэлектрическая проницаемость ионосферы будет изменяться плавно, и траектория радиоволны примет форму кривой линии.

Из найденного условия полного отражения следует:

1. С увеличением частоты падающей на ионосферу радиоволны под заданным углом отражение будет происходить от областей с большей электронной концентрацией, то есть, на больших высотах (рисунок 19).

Рисунок 18 − Слоистая модель ионосферы

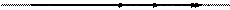
Рисунок 19 − Отражение от ионосферы радиоволн с различной частотой

Поскольку электронная концентрация изменяется скачками от слоя к слою, то при фиксированном угле падения будут существовать и соответствующие значения максимальных частот, при которых волна еще отражается от соответствующего слоя. Эти частоты называются максимально применимыми частотами (МПЧ). Величины МПЧ зависят от концентрации электронов в слое и угла падения 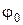. 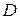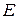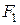Для соответствующих слоев их обозначают с указанием -МПЧ, -МПЧ, -МПЧ, 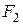-МПЧ. Наибольшая из всех МПЧ является максимально применимой частотой трассы заданной протяженности. Для волн с частотой условие отражения не выполняется и они проходят сквозь ионосферный слой.

2. При определенной электронной концентрации радиоволна данной частоты отразится только в том случае, если угол падения равен или превышает величину, определяемую по формуле полного отражения. Чем больше электронная плотность , тем при меньших значениях угла 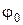, возможно отражение. Минимальный угол 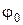, при котором в данных условиях еще возможно отражение, называют критическим углом (рисунок 20).

Рисунок 20 − Отражение от ионосферы радиоволн при разных углах падения

Частота, для которой критический угол равен нулю, называют критической частотой.

Очевидно, что критическая частота — это максимальная частота радиоволны, которая вертикально падает на ионосферу и отражается от нее. Критическая частота зависит от электронной концентрации и увеличивается с ростом ее электронной плотности. Полагая 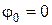, получим выражение для критической частоты

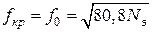
которое совпадает с найденным выше значением частоты, при котором 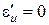. Это значит, что на критической частоте относительная диэлектрическая проницаемость ионосферы равна нулю.

Критическая частота и угол падения радиоволны на ионосферу однозначно определяют частоту радиоволны, которая падает на ионосферу под углом и отражается от нее. Действительно, преобразуем последние два выражения к виду

,

откуда

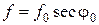
Отсюда следует, что при наклонном падении на ионосферу радиоволна может отразиться от нее на частоте, которая в 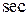раз превышает критическую частоту. Это соотношение называется законом секанса. Если рабочая частота больше частоты, определяемой по этому уравнению, то отражения не происходит и радиоволна, преломляясь в ионосфере, уходит в космическое пространство (рисунок 20).