Радиолинии с высокоподнятыми антеннами при гладкой сферической земле в зоне освещенности
На трассах УКВ-радиолиний протяженностью свыше 10 км необходимо при расчете учитывать сферичность земной поверхности, влияние которой проявляется прежде всего в ограничении дальности геометрической видимости между антеннами корреспондентов. При рассмотрении таких радиолиний в качестве весьма важного параметра выступает дальность прямой видимости 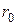 , т.е. расстояние между передающей и приемной антеннами, при котором прямая, их соединяющая, касается Земли (рисунок 0).
, т.е. расстояние между передающей и приемной антеннами, при котором прямая, их соединяющая, касается Земли (рисунок 0).
Из представленной на рисунке 0 модели дальность прямой видимости 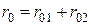 в силу того, что
в силу того, что 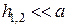 , может быть приближенно представлена в виде
, может быть приближенно представлена в виде 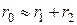 , где
, где 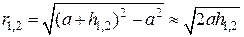 , и следовательно,
, и следовательно,
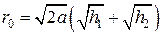 .
.
При прямолинейном распространении, т.е. без учета искривления траектории прямой волны в тропосфере (рефракции), полагая радиус Земли 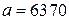 км, получаем
км, получаем
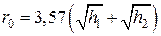 , [км].
, [км].
Отметим, что высота антенн выражена в метрах, а расстояние прямой видимости  − в километрах.
− в километрах.
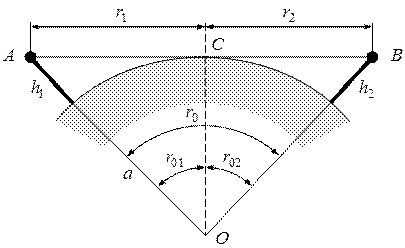
Рисунок 12 − Трассы над сферической поверхностью
При обычных высотах поднятия антенн (порядка нескольких десятков метров) предельное расстояние прямой видимости составляет несколько десятков километров.
При рассмотрении распространения радиоволн над гладкой сферической поверхностью Земли, например в условиях равнинной местности, пространство, в котором происходит распространение, в зависимости от его механизма подразделяется на две области — интерференции и дифракции (рисунок 13).
Область интерференции, называемая также освещенной, или областью прямой видимости, лежит на удалении от излучателя до 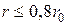 и характеризуется образованием поля в виде суперпозиции прямой и отраженной от земной поверхности волн.
и характеризуется образованием поля в виде суперпозиции прямой и отраженной от земной поверхности волн.
Область дифракции, лежащая на расстояниях 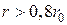 , характеризуется дифракционным распространением радиоволн и подразделяется, в свою очередь, на области (зоны) полутени
, характеризуется дифракционным распространением радиоволн и подразделяется, в свою очередь, на области (зоны) полутени  и тени
и тени 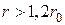 , различающиеся степенью ослабления и методом вычисления напряженности поля.
, различающиеся степенью ослабления и методом вычисления напряженности поля.
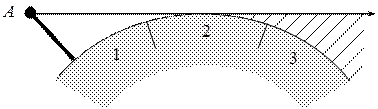
Рисунок 13 − Освещенная область (1), область полутени (2) и тени (3)
В области прямой видимости при высоте антенн 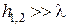 (рисунок ?) поле у приемной антенны, как и в случае распространения УКВ над плоской Землей, является результатом суперпозиции прямой и отраженной от земли волн. Напряженность поля и ее компоненты определяются выражениями, найденными выше для случая трасс над плоской поверхностью. В этих выражениях влияние сферичности земной поверхности учитывается заменой коэффициента отражения плоской волны от плоской поверхности раздела двух сред
(рисунок ?) поле у приемной антенны, как и в случае распространения УКВ над плоской Землей, является результатом суперпозиции прямой и отраженной от земли волн. Напряженность поля и ее компоненты определяются выражениями, найденными выше для случая трасс над плоской поверхностью. В этих выражениях влияние сферичности земной поверхности учитывается заменой коэффициента отражения плоской волны от плоской поверхности раздела двух сред 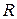 на эквивалентный коэффициент отражения, определяемый через коэффициент расходимости
на эквивалентный коэффициент отражения, определяемый через коэффициент расходимости
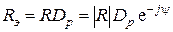 .
.
При такой замене сохраняются и интерференционные формулы для определения множителя ослабления 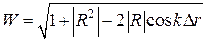 ,
, 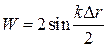 . В силу большой протяженности области, существенной для отражения, вдоль трассы, при значительных (близких к прямой видимости) расстояниях между корреспондентами становится существенным влияние кривизны земной поверхности. Если при отражении от плоскости (рисунок ?) телесные углы, заключающие в себе соответственно падающие и отраженные волны, равны, то при отражении от сферической поверхности телесный угол, охватывающий отраженные волны, больше телесного угла падающих волн. Поэтому плотность потока энергии отраженных волн, а значит, и коэффициент отражения меньше, чем при отражении от плоской Земли. На рисунке пунктиром обозначены лучи, отраженные от плоскости, сплошной линией – отраженные от сферической поверхности.
. В силу большой протяженности области, существенной для отражения, вдоль трассы, при значительных (близких к прямой видимости) расстояниях между корреспондентами становится существенным влияние кривизны земной поверхности. Если при отражении от плоскости (рисунок ?) телесные углы, заключающие в себе соответственно падающие и отраженные волны, равны, то при отражении от сферической поверхности телесный угол, охватывающий отраженные волны, больше телесного угла падающих волн. Поэтому плотность потока энергии отраженных волн, а значит, и коэффициент отражения меньше, чем при отражении от плоской Земли. На рисунке пунктиром обозначены лучи, отраженные от плоскости, сплошной линией – отраженные от сферической поверхности.

Рисунок 14 − Расходимость отраженных волн от сферической поверхности
Для учета этого уменьшения вводится коэффициент расходимости 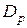 . Если обозначить через
. Если обозначить через 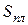 площадь сечения телесного угла пучка волн, отраженных в пределах плоской существенной области для отражения, а через
площадь сечения телесного угла пучка волн, отраженных в пределах плоской существенной области для отражения, а через  − то же, для случая сферической поверхности, то изменение плотности потока будет пропорционально отношению площадей
− то же, для случая сферической поверхности, то изменение плотности потока будет пропорционально отношению площадей 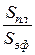 , а изменение напряженности поля −
, а изменение напряженности поля − 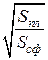 . Коэффициентом расхождения называют величину
. Коэффициентом расхождения называют величину 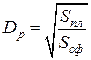 , которую определяют через под которым понимается взятое в некоторой фиксированной точке пространства отношение напряженностей полей волн, отраженных от идеально проводящих сферической и плоской поверхностей и определяемый через приведенные высоты и длину радиолинии:
, которую определяют через под которым понимается взятое в некоторой фиксированной точке пространства отношение напряженностей полей волн, отраженных от идеально проводящих сферической и плоской поверхностей и определяемый через приведенные высоты и длину радиолинии:
 .
.
Уменьшение напряженности поля отраженной волны за счет расхождения пучка лучей оценивают путем изменения модуля коэффициента отражения 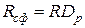 .
.
Разность хода прямой и отраженной волн 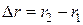 , входящая в выражения для множителя ослабления, а также угол скольжения
, входящая в выражения для множителя ослабления, а также угол скольжения 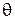 сохраняют свои значения, если вместо отражения от сферической земной поверхности рассматривать отражение от плоской, касательной к сфере в точке отражения, при одновременной замене истинных высот антенн
сохраняют свои значения, если вместо отражения от сферической земной поверхности рассматривать отражение от плоской, касательной к сфере в точке отражения, при одновременной замене истинных высот антенн 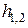 на приведенные
на приведенные 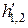 , отсчитываемые от плоскости (рисунок 15). Полученная в результате такой замены модель распространения радиоволн совпадает с распространением над плоской Землей, откуда следует, что расчетные формулы для определения разности хода
, отсчитываемые от плоскости (рисунок 15). Полученная в результате такой замены модель распространения радиоволн совпадает с распространением над плоской Землей, откуда следует, что расчетные формулы для определения разности хода 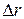 и угла скольжения
и угла скольжения 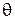 имеют тот же вид, что и при распространении над плоской Землей, если вместо истинных высот антенн
имеют тот же вид, что и при распространении над плоской Землей, если вместо истинных высот антенн 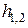 пользоваться приведенными
пользоваться приведенными 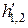 . Для определения этих высот необходимо провести плоскость
. Для определения этих высот необходимо провести плоскость 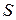 , касательную к сферической земной поверхности в точке отражения
, касательную к сферической земной поверхности в точке отражения 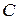 . Тогда разность хода над сферической поверхностью будет равна разности хода над плоскостью
. Тогда разность хода над сферической поверхностью будет равна разности хода над плоскостью 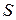 , и может быть рассчитана через высоты
, и может быть рассчитана через высоты 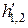 , отсчитываемые от плоскости и приближенно определяемые выражениями
, отсчитываемые от плоскости и приближенно определяемые выражениями
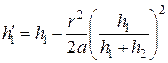 ,
, 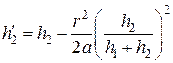 .
.

Рисунок 15 − Определение приведенной высоты антенн
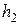 При указанной замене
При указанной замене 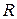 на
на 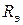 , и
, и 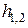 на
на 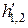 выражения для определения напряженности поля, ее составляющих и множителя ослабления, а также выводы о структуре поля у приемной антенны, полученные при рассмотрении распространения УКВ над плоской Землей, сохраняют силу и для случая распространения над гладкой сферической Землей в пределах области прямой видимости.
выражения для определения напряженности поля, ее составляющих и множителя ослабления, а также выводы о структуре поля у приемной антенны, полученные при рассмотрении распространения УКВ над плоской Землей, сохраняют силу и для случая распространения над гладкой сферической Землей в пределах области прямой видимости.
Таким образом, при расчете напряженности поля для радиолиний с гладкой сферической землей в зоне освещенности необходимо:
1. Проверить применимость формул для сферической земли в зоне освещенности по условию 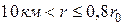 ;
;
2. Проверить применимость формул для гладкой земли по критерию Рэлея  ;
;
3. Определить вид формулы, по которой будет производиться расчет множителя ослабления: если 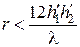 , то расчет производится по полной интерференционной формуле
, то расчет производится по полной интерференционной формуле
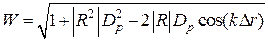 ,
,
где 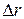 ,
, 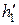 ,
, 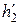 определяются по вышеприведенным формулам, а
определяются по вышеприведенным формулам, а
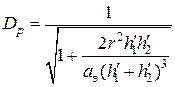 ,
,
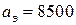 км − эквивалентный радиус Земли;
км − эквивалентный радиус Земли;
если 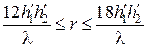 , то расчет производится по упрощенной интерференционной формуле
, то расчет производится по упрощенной интерференционной формуле 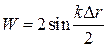 где
где 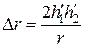 ;
;
если 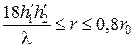 , то расчет производится по квадратичной формуле Введенского
, то расчет производится по квадратичной формуле Введенского 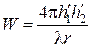 .
.
4. В соответствии с произведенным выбором рассчитать значение множителя ослабления.
5. Рассчитать напряженность поля в месте приема в соответствии с формулой 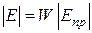 .
.
Дата добавления: 2015-10-19; просмотров: 2140;
