Пример 2. 3.1. Классификация погрешностей

ПОГРЕШНОСТИ ИЗМЕРЕНИЙ

3.1. Классификация погрешностей

Любые измерения направлены на получение результата, т.е. оценки истинного значения физической величины в принятых единицах. Вследствие несовершенства средств и методов измерений, воздействия внешних факторов и многих других причин результат каждого измерения неизбежно отягощен погрешностью.

Качество измерений тем выше, чем ближе результат измерения к истинному значению измеряемой величины. Значение ошибки никогда нельзя узнать точно, можно только оценить. Результат измерения может быть правильным только в определенной степени, поэтому информация об измерении оказывается осмысленной только в том случае, когда одновременно с результатом измерения имеются сведения об ошибке измерения. Результат измерения, не сопровождаемый указанием интервала значения ошибки, не содержит никакой информации.

Понятие “погрешность” – одно из центральных в метрологии.

Погрешность результата измерений – это разница между результатом измерений Х и истинным (или действительным) значением Q измеряемой величины

Она указывает границы неопределенности значения измеряемой величины.

Погрешность средства измерения – разность между показанием средства измерения и истинным (действительным) значением физической величины. Она характеризует точность результатов измерений, проводимых данным средством. Эти два понятия во многом близки друг к другу и классифицируются по одинаковым признакам. Погрешности измерений определяются главным образом погрешностями средств измерений, но они не тождественны им. Так, погрешности измерений, связанные с методом измерений, и личные ошибки экспериментатора следует относить только к погрешностям измерений, но не к погрешностям средств измерений.

Погрешности измерений могут быть вызваны различными причинами и по-разному проявляться в эксперименте. В связи с этим существенно отличаются и пути уменьшения тех или иных составляющих погрешности. Все это делает целесообразным классификацию погрешностей по тому или иному признаку.

В зависимости от характера и причин появления погрешности измерений и средств измерений делят на систематические (детерминированные), случайные (стохастические) и прогрессирующие. Различают ещё грубые погрешности и промахи.

Случайная погрешность– составляющая погрешности измерения, которая при повторении измерений изменяется случайным образом. Случайные погрешности могут быть обнаружены при повторных измерениях одной и той же величины, когда получаются неодинаковые результаты. Их нельзя исключить (так как неизвестны причины, их вызвавшие), но их влияние на результат измерения может быть теоретически учтено при обработке результатов измерений методами теории вероятностей и математической статистики.

Для получения результата, минимально отличающегося от истинного значения измеряемой величины, проводят многократные измерения требуемой величины с последующей математической обработкой экспериментальных данных.

Систематическая погрешность– составляющая погрешности измерения, которая при повторении равноточных измерений неизменного размера остается постоянной или закономерно изменяется. Систематические погрешности могут быть изучены, при этом результат измерения может быть уточнен или путем внесения поправок, если числовые значения этих погрешностей определены, или путем применения таких способов измерения, которые дают возможность исключить влияние систематических погрешностей без их определения. Числовые значения систематических погрешностей определяются путем поверки средств измерений.

Прогрессирующая (дрейфовая) погрешность– это непредсказуемая погрешность, медленно меняющаяся во времени. Впервые это понятие введено в 1949 г. М.Ф.Маликовым в монографии “Основы метрологии”. Отличительными особенностями такой погрешности являются:

- возможность коррекции поправками только в данный момент времени, а далее они вновь непредсказуемо изменяются;

- изменение этой погрешности во времени – нестационарный случайный процесс, и поэтому в рамках теории случайных процессов может быть описан лишь с определенными оговорками.

Прогрессирующая погрешность может возникнуть вследствие как непостоянства во времени текущего математического ожидания нестационарного случайного процесса, так и изменения во времени его дисперсии или формы закона распределения.

Грубая погрешность –случайнаяпогрешность, существенно превышающая ожидаемую. Результаты с грубыми погрешностями обнаруживают и исключают из рассмотрения. Они, как правило, возникают из-за ошибок или неправильных действий оператора (его психофизиологического состояния, неверного отсчета, ошибок в записях или вычислениях, неправильного включения приборов или сбоев в их работе и др.). Возможной причиной возникновения промахов также могут быть кратковременные резкие изменения условий проведения измерений. Если промахи обнаруживаются в процессе измерений, то результаты, их содержащие, отбрасывают. Однако чаще промахи выявляют при окончательной обработке результатов.

В зависимости от формы числового выражения погрешности независимо от вида (систематические или случайные) различают: абсолютные и относительные– для измерений; абсолютные, относительные и приведенные – для средств измерений.

Абсолютная погрешность Δx –это разность между измеренной величиной x_ном(показанием прибора x_п) и действительным значением Q измеряемой величины, т.е. для измерений

Δx=x_ном-Q (3.1)

a для прибора Δx=x_п-Q (3.2).

Абсолютная погрешность не может в полной мере служить показателем точности измерений, т.к. одно и то же значение, например Δx=0,05 мм при Х=100 мм соответствует достаточно высокой точности измерений, а при Х=1 мм – низкой. Поэтому вводится понятие относительной погрешности.

относительная погрешность является более информативной (в %), которая с учетом выражений (3.1) и (3.2) определяется как

δ_x=(Δx/Q)·100 (3.3)

Удобно использовать выражение

δ_x=Δx/x_номилиδx=Δx/x_п , (3.4)

Так как значения x_ном или x_пизвестны, а разница между (3.3) и (3.4) является величиной высшего порядка малости.

Эта наглядная характеристика точности результата измерения не годится для нормирования погрешности средства измерений, т.к. при измерении Q принимает различные значения вплоть до бесконечности при Q=0. В связи с этим для указания и нормирования погрешности средств измерений используется ещё одна разновидность погрешности – приведенная.

Приведенная погрешность (в %) выражается как отношение абсолютной погрешности к нормирующему значению Q_N :

γ= ( Δx/Q_N)·100(3.5)

При этом Q_N выбирают равным:

большему из пределов измерений, если нулевое значение х является началом шкалы или находится вне диапазона измерений;

большему из модулей пределов измерений, если нулевое значение находится внутри диапазона измерений (для электроизмерительных приборов -– сумме модулей пределов измерений);

модулю разности пределов измерений, если шкала принята с условным нулем (шкала в ºС);

номинальному значению для средств измерений с номинальным значением измеряемой величины (частотомер с диапазоном измерений 45…55 Гц с f_ном =50 Гц);

всей длине шкалы или её части, соответствующей диапазону измерений (при этом абсолютную погрешность выражают также в единицах длины).

В зависимости от причин возникновения погрешности делятся на инструментальные, методические, и субъективные (личные).

Инструментальная погрешность измерения – погрешность из-за несовершенства средств измерений. Эта погрешность в свою очередь обычно подразделяется на основную погрешность средств измерения и дополнительную.

Основная погрешность средства измерений – это погрешность в условиях, принятых за нормальные, т.е. нормальных значениях всех величин, влияющих на результат измерения (температуры, влажности, напряжения питания и др.). Дополнительная погрешность возникает при отличии значений влияющих величин от нормальных. Обычно различают отдельные составляющие дополнительной погрешности, например, температурную погрешность, погрешность из-за изменения напряжения питания и т.п.

Методическая погрешность – погрешность измерения, происходящая из-за несовершенства метода измерений. Эта погрешность может возникать из-за принципиальных недостатков используемого метода, из-за неполноты знаний о происходящих при измерении процессах, из-за неточности применяемых расчетных формул. Если предел допускаемой инструментальной погрешности средств измерений нормируется соответствующими документами, то методическая погрешность может и должна быть оценена только самим экспериментатором с учетом конкретных условий эксперимента, что во многих случаях представляет собой достаточно сложную задачу.

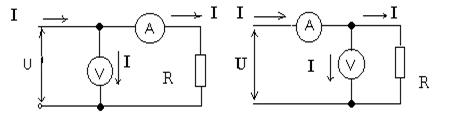Пример 1.

а) б)

I_а – ток, измеряемый амперметром;

I_н – ток, протекающий через сопротивление нагрузки;

I_v – ток, протекающий через вольтметр;

Р_н - действительное значение измеряемой мощности.

Измеренное значение в случае а):

Р=IU_н=(I_н +I_v)U_н=I_нU_н+I_vU_н=P_н+I_vU_н.

Абсолютная погрешность D_р=Р-Р_н= P_н+I_vU_н -P_н= I_vU_н.

Относительная погрешность

d_р1=D_р/Р_н = I_vU_н/ I_нU_н= I_v/ I_н=(U_н/R_v)/(U_н/R_н)= R_н/ R_v.

d_р1® 0 при R_н® 0 или R_v® ¥.

Измеренное значение в случае б)

Р=I_нU=I_н (U_н+U_а) =I_нU_н+I_нU_а=P_н+I_нU_а.

Абсолютная погрешность D_р=Р-Р_н= P_н+I_нU_а -P_н= I_нU_а.

Относительная погрешность

d_р2=D_р/Р_н = I_нU_а/ I_нU_н= U_а/ U_н =( I_нR_а)/( I_нR_н)= R_а/ R_н.

d_р2® 0 при R_а® 0 или R_н® ¥.

d_р1=d_р2 Þ R_н/ R_v= R_а/ R_н Þ R_н=Ö R_а R_v.

При R_а=0,002 Ом; R_v=1000 Ом; R_н=1,41 Ом; d_р=0,14%.

Субъективная, или личная, погрешность обусловлена индивидуальными особенностями лица, выполняющего измерения. Примерами таких погрешностей являются погрешности из-за неправильного отсчитывания десятых долей деления шкалы прибора, асимметричной установки штриха оптического индикатора между двумя рисками, запаздывание реакции человека на сигнал. Автоматизация средств измерений и совершенствование конструкций отсчетных устройств и органов регулировки и управления привели к тому, что субъективные погрешности обычно незначительны, например, в цифровых приборах они практически отсутствуют.

Пример 2.

Пусть цена деления равномерной шкалы равна х_д единиц измеряемой физической величины, длина деления L мм. Определить наибольшее значение личной погрешности.

При условии, что средний оператор может интерполировать в пределах деления шагами по 0,2 деления, т.е. по 0,2L, то наибольшее значение личной погрешности: D_л=(х_д·0,2L)/L=0,2х_д.

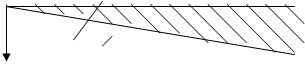
Если произвести поверку средства измерения, т.е. определить его основную погрешность в ряде точек шкалы, и построить зависимость абсолютной погрешности от показаний прибора, то эта зависимость может иметь двоякий характер: все значения погрешности могут оказаться в пределах прямых 1 (рис.1), параллельных оси абсцисс, или значения погрешности закономерно изменяются в пределах прямых 2.

В рассматриваемом случае погрешность Δхприбора может быть представлена двучленным уравнением

Δх=|а₀|+|в₀х|, (3.6)

где а₀– аддитивная погрешность (погрешность нуля);

в₀х - мультипликативная погрешность (погрешность чувствительности).