Течение несжимаемой жидкости через недеформируемый пласт

В данном случае k=const, r=const , h=const,

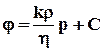. 3.11

Следовательно:

распределение давления

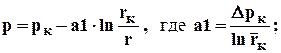3.19

градиент давления

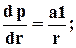3.20

объёмный дебит (формула Дюпюи)

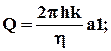3.21

скорость фильтрации

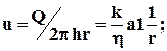3.22

закон движения частиц флюида

Движение частицы описывается уравнением .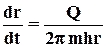

Интегрируем данное соотношение по времени от 0 до tи по расстоянию от R₀до r, где R₀- начальное положение частицы флюида. В результате получим

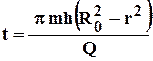. 3.23

Время отбора всей жидкости из кругового пласта

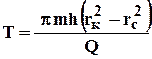. 3.24

* средневзвешенное давление

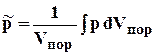. 3.25

С целью получения выражения для средневзвешенного давления определим

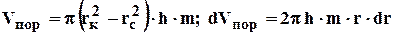3.26

и, подставив в (3.25) выражение (3.19), проинтегрируем от r_cдо r_к. Пренебрегая r_спо сравнению с r_к получим

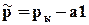. 3.27

Анализ:

Дебит не зависит от r, а только от депрессии d р_к. График зависимости Qот d р_к (Рис.3.4) называется индикаторной диаграммой, а сама зависимость - индикаторной. Отношение дебита к депрессии называется коэффициентом продуктивности скважины

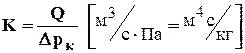. 3.28

2. Градиент давления и скорость обратно пропорциональны расстоянию (рис.3.5) и образуют гиперболу с резким возрастанием значений при приближении к забою.

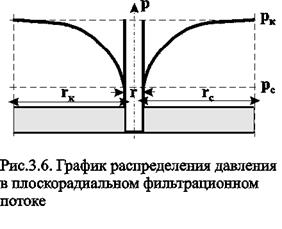
3. Графиком зависимости р=р( r ) является логарифмическая кривая

(рис.3.6), вращением которой вокруг оси скважины образуется поверхность, называемая воронкой депрессии. Отсюда, основное влияние на дебит оказывает состояние призабойной зоны, что и обеспечивает эффективность методов интенсификации притока.

4. Изобары - концентрические, цилиндрические поверхности, ортогональные траекториям.

1. Дебит слабо зависит от величины радиуса контура r_кдля достаточно больших значений r_к /r_c, т.к. r_к /r_c входят в формулу под знаком логарифма.