Модельных экспериментов
Эффективность использования экспериментальных ресурсов при математическом моделировании существенным образом зависит от выбора плана эксперимента. Причин этого две:
- план эксперимента в значительной степени определяет порядок статистического анализа его результатов;
- успешность разрешения с помощью эксперимента поставленных экспериментатором вопросов существенно зависит от его плана.
Основная цель моделирования состоит в возможно более глубоком изучении поведения моделируемой системы при минимальных затратах. С этой целью необходимо планировать и проектировать не только саму модель, но и процесс ее использования, то есть проведения на ней экспериментов.
Итак, основная задача планирования машинных экспериментов – получение необходимой информации об исследуемой системе S при ограничениях на ресурсы [34]. К числу частных задач, решаемых при планировании машинных экспериментов, относятся задачи уменьшения затрат машинного времени на моделирование, увеличения точности и достоверности результатов моделирования, проверки адекватности модели и т.д. [34,35].
Важное значение при планировании эксперимента имеют следующие обстоятельства:
- простота повторения условий эксперимента на ПК с моделью;
- возможность управления экспериментом, включая его прерывание и возобновление;
- легкость варьирования условий (воздействий внешней среды Е);
- наличие корреляции между последовательностью точек в процессе моделирования.
Рассмотрим эти обстоятельства более подробно.
Преимуществом машинных экспериментов перед натурными является возможность полного воспроизведения условий эксперимента с моделью. Сравнивать две альтернативы возможно при одинаковых условиях, что достигается, например, выбором одной и той же последовательности случайных чисел для каждой из альтернатив.
Существенным достоинством является также простота прерывания и возобновления машинных экспериментов, что позволяет применять последовательные и эвристические приемы планирования, которые могут оказаться нереализуемыми в экспериментах с реальными объектами. При работе с машинной моделью 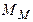 всегда возможно прерывание эксперимента на время, необходимое для анализа результатов и принятия решений о его дальнейшем ходе.
всегда возможно прерывание эксперимента на время, необходимое для анализа результатов и принятия решений о его дальнейшем ходе.
Недостатком машинных экспериментов является то, что часто возникают трудности, связанные с наличием корреляции в выходных последовательностях, то есть результаты одних наблюдений зависят от результата одного или нескольких предыдущих, и поэтому в них содержится меньше информации, чем в независимых наблюдениях. Так как в большинстве существующих методах планирования экспериментов предполагается независимость наблюдений, то многие из них нельзя непосредственно применять для машинных экспериментов при наличии корреляции.
Рассмотрим основные понятия теории планирования эксперимента. В связи с тем, что математические методы планирования экспериментов основаны на кибернетическом представлении процесса проведения эксперимента, наиболее подходящей моделью последнего является абстрактная схема, называемая «черным ящиком». При этом подходе различают входные 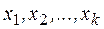 и выходные
и выходные 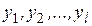 переменные. В зависимости от того, какую роль играет каждая переменная в проводимом эксперименте, она может являться либо фактором, либо реакцией. Пусть, например, имеют место только две переменные
переменные. В зависимости от того, какую роль играет каждая переменная в проводимом эксперименте, она может являться либо фактором, либо реакцией. Пусть, например, имеют место только две переменные 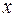 и
и 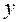 . Тогда, если цель эксперимента – изучение влияния переменной
. Тогда, если цель эксперимента – изучение влияния переменной 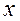 на переменную
на переменную 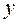 , то
, то 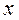 - фактор, а
- фактор, а 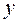 - реакция. В экспериментах с машинными моделями
- реакция. В экспериментах с машинными моделями 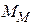 фактор является экзогенной или управляемой (входной) переменной, а реакция – эндогенной (выходной) переменной.
фактор является экзогенной или управляемой (входной) переменной, а реакция – эндогенной (выходной) переменной.
Каждый фактор 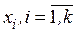 может принимать в эксперименте одно из нескольких значений, называемых уровнями. Фиксированный набор уровней факторов определяет одно из возможных состояний рассматриваемой системы. Одновременно этот набор представляет собой условия проведения одного из возможных экспериментов.
может принимать в эксперименте одно из нескольких значений, называемых уровнями. Фиксированный набор уровней факторов определяет одно из возможных состояний рассматриваемой системы. Одновременно этот набор представляет собой условия проведения одного из возможных экспериментов.
Каждому фиксированному набору уровней факторов соответствует определенная точка в многомерном пространстве, называемом факторным пространством. Эксперименты не могут быть реализованы во всех точках факторного пространства, а лишь в принадлежащих допустимой области, как это показано на рис.16.1 для случая двух факторов (плоскость 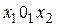 ).
).

Существует связь между уровнями факторов и реакцией (откликом) системы, которую можно представить в виде соотношения
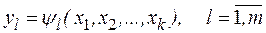 .
.
Функцию 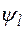 , связывающую реакцию с факторами, называют функцией реакции, а геометрический образ, соответствующий функции реакции – поверхностью реакции. Заранее вид зависимостей
, связывающую реакцию с факторами, называют функцией реакции, а геометрический образ, соответствующий функции реакции – поверхностью реакции. Заранее вид зависимостей 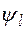 не известен, поэтому используют приближенные соотношения
не известен, поэтому используют приближенные соотношения
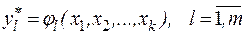 .
.
Зависимости 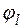 находятся по данным эксперимента. Последний необходимо поставить так, чтобы при минимальных затратах ресурсов, варьируя значения факторов, можно было построить адекватную математическую модель системы и оценить ее характеристики.
находятся по данным эксперимента. Последний необходимо поставить так, чтобы при минимальных затратах ресурсов, варьируя значения факторов, можно было построить адекватную математическую модель системы и оценить ее характеристики.
При планировании экспериментов необходимо определить основные свойства факторов, которые при проведении эксперимента могут быть управляемыми и неуправляемыми, наблюдаемыми и ненаблюдаемыми, изучаемыми и не изучаемыми, количественными и качественными, фиксированными и случайными.
Фактор называют управляемым, если его уровни целенаправленно выбираются в процессе эксперимента. При машинной реализации модели 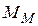 исследователь принимает решения, управляя изменением в допустимых пределах различных факторов.
исследователь принимает решения, управляя изменением в допустимых пределах различных факторов.
Фактор называется наблюдаемым или первичным, если его значения наблюдаются и регистрируются, а экспериментатор непосредственно заинтересован в исследовании влияния этого фактора. Обычно в машинном эксперименте с моделью 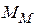 наблюдаемые факторы совпадают с управляемыми, так как нерационально управлять фактором, не наблюдая его. Но неуправляемый фактор тоже можно наблюдать. Например, на этапе проектирования конкретной системы S нельзя управлять заданными воздействиями внешней среды Е, но можно наблюдать их в машинном эксперименте.
наблюдаемые факторы совпадают с управляемыми, так как нерационально управлять фактором, не наблюдая его. Но неуправляемый фактор тоже можно наблюдать. Например, на этапе проектирования конкретной системы S нельзя управлять заданными воздействиями внешней среды Е, но можно наблюдать их в машинном эксперименте.
Наблюдаемые неуправляемые факторы получили название сопутствующих или вторичных. Обычно при машинном эксперименте число сопутствующих факторов велико, поэтому рационально учитывать влияние лишь тех из них, которые наиболее существенно воздействуют на интересующую исследователя реакцию.
Фактор является количественным, если его значения – числовые величины, влияющие на реакцию, а в противном случае фактор называется качественным. Например, в модели системы, формализуемой в виде схемы массового обслуживания, количественными факторами являются интенсивности входящих потоков заявок, интенсивности потоков обслуживания, емкости накопителей, количество обслуживающих каналов и т.д., а качественными факторами – дисциплины постановки в очередь, выбора из очереди, обслуживания заявок каналами и пр. Качественным факторам, в отличие от количественных, не соответствует числовая шкала. Однако и для них можно построить условную порядковую шкалу, с помощью которой производится кодирование, устанавливая соответствие между условиями качественного фактора и числами натурального ряда.
Фактор называется фиксированным, если в эксперименте исследуются все интересующие экспериментатора значения фактора, а если экспериментатор исследует только некоторую случайную выборку из совокупности интересующих значений факторов, то фактор называется случайным. На основании случайных факторов могут быть сделаны выводы и о тех значениях факторов, которые в эксперименте не исследовались.
Основными требованиями, предъявляемыми к факторам, является требование управляемости фактора и требование непосредственного воздействия на объект.
Под управляемостью понимается возможность установки и поддержания выбранного нужного уровня фактора постоянным в течение всего испытания или изменяющимся в соответствии с заданной программой.
Требование непосредственного воздействия на объект имеет большое значение в связи с тем, что трудно управлять фактором, если он является функцией других факторов.
При планировании эксперимента может возникнуть ситуация, когда одновременно изменяются несколько факторов. Определим требования, которые предъявляются к совокупности факторов. Основные из них – совместимость и независимость. Первое означает, что все комбинации факторов осуществимы, а второе – соответствует возможности установления фактора на любом уровне независимо от уровней других.
При проведении машинного эксперимента с моделью 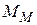 для оценки некоторых характеристик процесса функционирования исследуемой системы S экспериментатор стремится создать такие условия, которые способствуют выявлению влияния факторов, находящихся в функциональной связи с искомой характеристикой. Для этого необходимо:
для оценки некоторых характеристик процесса функционирования исследуемой системы S экспериментатор стремится создать такие условия, которые способствуют выявлению влияния факторов, находящихся в функциональной связи с искомой характеристикой. Для этого необходимо:
- отобрать факторы 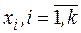 , влияющие на искомую характеристику и описать функциональную зависимость;
, влияющие на искомую характеристику и описать функциональную зависимость;
-установить диапазон изменения факторов 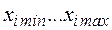 ;
;
- определить координаты точек факторного пространства 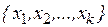 , в которых следует проводить эксперимент;
, в которых следует проводить эксперимент;
- оценить необходимое число реализаций и их порядок в эксперименте.
Свойства объекта исследования, то есть процесса машинного моделирования системы S, можно описывать с помощью различных методов (моделей планирования).
Наибольшее применение нашли модели в виде алгебраических полиномов.
Предполагаем, что изучается влияние 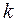 количественных факторов
количественных факторов 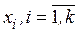 на некоторую реакцию
на некоторую реакцию 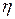 в отведенной для экспериментирования локальной области факторного пространства
в отведенной для экспериментирования локальной области факторного пространства 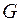 , ограниченной
, ограниченной 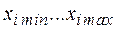 ,
, 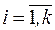 для случая
для случая 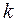 = 2. Допустим, что функцию реакции
= 2. Допустим, что функцию реакции 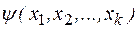 можно с некоторой степенью точности представить в виде полинома степени
можно с некоторой степенью точности представить в виде полинома степени 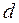 от
от 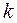 переменных:
переменных:
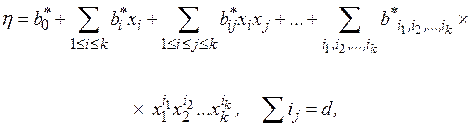 ,
,
который содержит 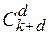 коэффициентов.
коэффициентов.
Последнее соотношение может быть представлено как
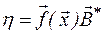 ,
,
где 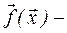 вектор с элементами
вектор с элементами 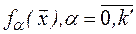 , входящими в исходный полином;
, входящими в исходный полином;
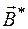 - вектор коэффициентов, которые соответственно имеют вид
- вектор коэффициентов, которые соответственно имеют вид
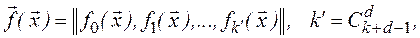
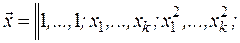
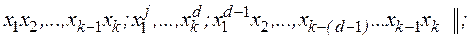
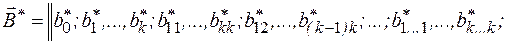
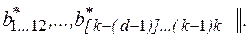
Введем фиктивную переменную 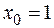 , а также переменные
, а также переменные
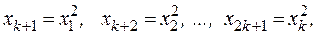
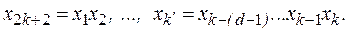
Тогда полином для функции реакции запишется как однородное линейное уравнение вида
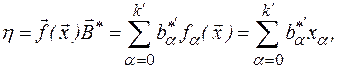
где
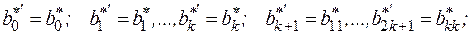
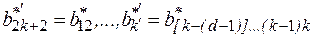 .
.
Для оценки коэффициентов можно применить методы линейной регрессии.
Функция реакции может иметь и более сложную зависимость от факторов. В этом случае некоторые из них удается привести к линейному виду. Такими моделями являются мультипликативная регрессионная, экспоненциальная и пр.
Если выбрана модель планирования и записано ее уравнение, то остается в отведенной для исследования области факторного пространства 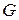 спланировать и провести эксперимент для оценки числовых значений коэффициентов этого уравнения.
спланировать и провести эксперимент для оценки числовых значений коэффициентов этого уравнения.
Так как последнее выражение для полинома функции реакции содержит 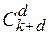 коэффициентов, подлежащих определению, то план эксперимента
коэффициентов, подлежащих определению, то план эксперимента 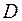 должен содержать по крайней мере
должен содержать по крайней мере 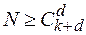 различных экспериментальных точек:
различных экспериментальных точек:
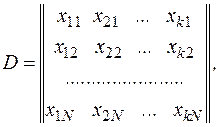
где 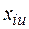 - значения, которые принимает
- значения, которые принимает 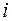 -я переменная в
-я переменная в 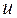 -м испытании,
-м испытании, 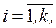
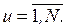
Реализовав испытания в 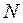 точках области факторного пространства, отведенной для экспериментирования, получим вектор наблюдений, имеющий вид
точках области факторного пространства, отведенной для экспериментирования, получим вектор наблюдений, имеющий вид
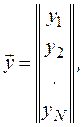
где 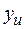 - реакция, соответствующая
- реакция, соответствующая 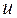 -й точке плана
-й точке плана 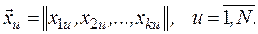
При незначительном влиянии неуправляемых входных переменных и параметров по сравнению с вводимыми возмущениями управляемых переменных в планировании эксперимента предполагается верной следующая модель:
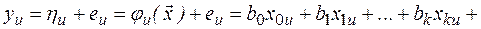
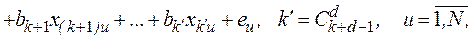
где 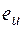 - ошибка (флуктуация) испытания, которая предполагается независимой нормально распределенной случайной величиной с нулевым математическим ожиданием и постоянной дисперсией.
- ошибка (флуктуация) испытания, которая предполагается независимой нормально распределенной случайной величиной с нулевым математическим ожиданием и постоянной дисперсией.
В случае если моделирование используется как инструмент принятия решения в роли функции реакции выступает показатель эффективности, который в этом случае является скалярной величиной 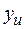 = y и называется наблюдаемой переменной (
= y и называется наблюдаемой переменной ( 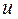 =1). Тогда аналитическое выражение для модели планирования предстанет в виде
=1). Тогда аналитическое выражение для модели планирования предстанет в виде
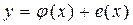 ,
,
где х – точка в факторном пространстве (определённое сочетание уровней факторов). Так как 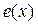 является случайной величиной, то и
является случайной величиной, то и 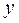 случайная переменная. Её дисперсия, характеризующая точность измерений и называемая в теории планирования дисперсией воспроизводимости эксперимента, равна дисперсии ошибки
случайная переменная. Её дисперсия, характеризующая точность измерений и называемая в теории планирования дисперсией воспроизводимости эксперимента, равна дисперсии ошибки 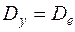 . Модельный эксперимент считается идеальным при
. Модельный эксперимент считается идеальным при 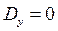 .
.
Рассмотрим особенности планирования эксперимента для линейного приближения поверхности реакции. Построению плана предшествует проведение ряда неформализованных действий (принятие решений), направленных на выбор локальной области факторного пространства 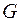 .
.
Вначале следует выбрать границы 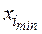 и
и 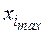 области определения факторов, задаваемые исходя из свойств исследуемого объекта, то есть на основе априорной информации о системе S и внешней среде
области определения факторов, задаваемые исходя из свойств исследуемого объекта, то есть на основе априорной информации о системе S и внешней среде 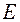 . Например, такая переменная, как температура, при термобарических экспериментах принципиально не может быть ниже абсолютного нуля и выше температуры плавления материала, из которого изготовлена термобарокамера.
. Например, такая переменная, как температура, при термобарических экспериментах принципиально не может быть ниже абсолютного нуля и выше температуры плавления материала, из которого изготовлена термобарокамера.
После определения области 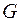 необходимо найти локальную подобласть для планирования эксперимента путем выбора основного (нулевого) уровня
необходимо найти локальную подобласть для планирования эксперимента путем выбора основного (нулевого) уровня 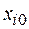 , который часто называют центром плана и интервалов варьирования
, который часто называют центром плана и интервалов варьирования 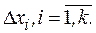 В качестве исходной точки
В качестве исходной точки 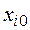 выбирают такую, которая соответствует наилучшим условиям, определенным на основе анализа априорной информации о системе S. Причем эта точка не должна лежать близко к границам области определения факторов
выбирают такую, которая соответствует наилучшим условиям, определенным на основе анализа априорной информации о системе S. Причем эта точка не должна лежать близко к границам области определения факторов 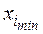 и
и 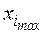 . На выбор интервала варьирования накладываются естественные ограничения снизу (интервал не может быть меньше ошибки фиксирования уровня фактора, так как в противном случае верхний и нижний уровни окажутся неразличимыми) и сверху (верхний и нижний уровни не должны выходить за область определения
. На выбор интервала варьирования накладываются естественные ограничения снизу (интервал не может быть меньше ошибки фиксирования уровня фактора, так как в противном случае верхний и нижний уровни окажутся неразличимыми) и сверху (верхний и нижний уровни не должны выходить за область определения 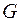 ).
).
В рамках выбранной модели планирования в виде алгебраических полиномов строится план эксперимента путем варьирования каждого из факторов 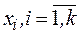 на нескольких уровнях
на нескольких уровнях 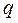 относительно центра плана
относительно центра плана 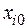 .
.
Эксперимент, в котором реализуются все возможные сочетания уровней факторов, называется полным факторным экспериментом (ПФЭ).
Число различных комбинаций уровней в ПФЭ для 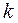 факторов
факторов
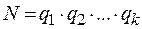 .
.
При одинаковом числе уровней для всех 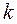 факторов
факторов 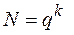 .
.
Если выбранная модель планирования включает в себя только линейные члены полинома и их произведения, то для оценки коэффициентов модели используется план эксперимента с варьированием всех 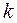 факторов на двух уровнях, то есть
факторов на двух уровнях, то есть 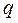 = 2. Такие планы называются планами типа
= 2. Такие планы называются планами типа 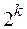 , где
, где 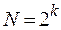 - число всех возможных испытаний.
- число всех возможных испытаний.
 Начальный этап планирования эксперимента для получения коэффициентов линейной модели основан на варьировании факторов на двух уровнях: нижнем
Начальный этап планирования эксперимента для получения коэффициентов линейной модели основан на варьировании факторов на двух уровнях: нижнем 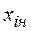 и верхнем
и верхнем 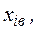 симметрично расположенных относительно центра плана
симметрично расположенных относительно центра плана 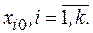 Геометрическая интерпретация показана на рис. 16.2.
Геометрическая интерпретация показана на рис. 16.2.
Так как каждый фактор принимает лишь два значения: 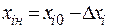 и
и 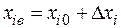 , то для упрощения записи условий каждого испытания масштабы по осям факторов выбираются так, чтобы нижний уровень соответствовал –1, верхний - +1, а основной – нулю с помощью преобразования вида
, то для упрощения записи условий каждого испытания масштабы по осям факторов выбираются так, чтобы нижний уровень соответствовал –1, верхний - +1, а основной – нулю с помощью преобразования вида
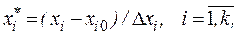
где 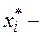 кодированное значение
кодированное значение 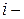 го фактора;
го фактора; 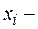 натуральное значение фактора;
натуральное значение фактора; 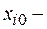 центр плана;
центр плана; 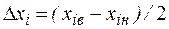 - интервал варьирования фактора.
- интервал варьирования фактора.
 Расположение точек для ПФЭ типа 22 показано на рис. 16.3. Выписывая комбинации уровней факторов для каждой экспериментальной точки квадрата, получим план
Расположение точек для ПФЭ типа 22 показано на рис. 16.3. Выписывая комбинации уровней факторов для каждой экспериментальной точки квадрата, получим план 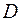 полного факторного эксперимента типа 22
полного факторного эксперимента типа 22
Для трех факторов, каждый из которых имеет только максимальный и минимальный уровни, реакция системы будет иметь вид
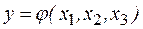 .
.
Определить зависимость 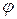 можно, построив математическую (аналитическую) модель планирования в виде полинома первого порядка
можно, построив математическую (аналитическую) модель планирования в виде полинома первого порядка
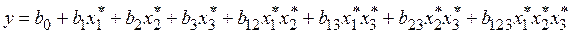 .
.
Для оценки свободного члена 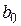 и определения эффектов взаимодействия
и определения эффектов взаимодействия 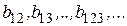 план эксперимента
план эксперимента 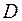 расширяют до матрицы планирования
расширяют до матрицы планирования 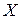 путем добавления соответствующей «фиктивной переменной»: единичного столбца
путем добавления соответствующей «фиктивной переменной»: единичного столбца 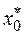 и столбцов произведений
и столбцов произведений 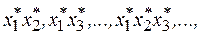 Количество испытаний в ПФЭ превосходит число определяемых коэффициентов линейной модели плана эксперимента, то есть ПФЭ обладает избыточностью, откуда большие временные затраты на его подготовку и проведение. Так, например, при наличии в модели 3-х факторов, имеющих каждый 4-е уровня, получаем
Количество испытаний в ПФЭ превосходит число определяемых коэффициентов линейной модели плана эксперимента, то есть ПФЭ обладает избыточностью, откуда большие временные затраты на его подготовку и проведение. Так, например, при наличии в модели 3-х факторов, имеющих каждый 4-е уровня, получаем 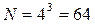 эксперимента. Если каждый из них длится хотя бы 1 минуту, то на однократную реализацию ПФЭ потребуется более часа. Отсюда правило: использование ПФЭ целесообразно только в том случае, если в ходе имитационного эксперимента исследуется взаимное влияние всех факторов, фигурирующих в модели.
эксперимента. Если каждый из них длится хотя бы 1 минуту, то на однократную реализацию ПФЭ потребуется более часа. Отсюда правило: использование ПФЭ целесообразно только в том случае, если в ходе имитационного эксперимента исследуется взаимное влияние всех факторов, фигурирующих в модели.
Вдвое сократить количество экспериментов сравнительно с ПФЭ позволяет план дробного факторного эксперимента (ДФЭ).
Пусть имеется простейший ПФЭ типа 22. Полином первого порядка и матрица планирования для этого случая имеют соответственно вид
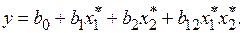
Если в выбранных интервалах варьирования уровней процесс можно описать линейной моделью, то достаточно определить три коэффициента 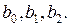 Таким образом, остается одна степень свободы, которую можно использовать для минимизации числа испытаний. При линейном приближении
Таким образом, остается одна степень свободы, которую можно использовать для минимизации числа испытаний. При линейном приближении 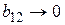 и вектор-столбец
и вектор-столбец 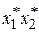 можно использовать для нового фактора
можно использовать для нового фактора 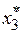 . Так как при постулировании линейной модели все парные взаимодействия не учитывают, то для предыдущего случая трех факторов вместо восьми испытаний в ПФЭ типа
. Так как при постулировании линейной модели все парные взаимодействия не учитывают, то для предыдущего случая трех факторов вместо восьми испытаний в ПФЭ типа 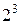 необходимо провести только четыре. Отсюда правило проведения дробного факторного эксперимента формулируется так: для сокращения числа испытаний новому фактору присваивается значение вектора-столбца матрицы, принадлежащего взаимодействию, которым можно пренебречь.
необходимо провести только четыре. Отсюда правило проведения дробного факторного эксперимента формулируется так: для сокращения числа испытаний новому фактору присваивается значение вектора-столбца матрицы, принадлежащего взаимодействию, которым можно пренебречь.
Таким образом, при проведении эксперимента из четырех испытаний для оценки влияния трех факторов пользуются половиной ПФЭ типа 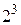 , так называемой полурепликой.
, так называемой полурепликой.
Если приравнять 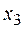 и
и 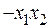 , то можно получить вторую полуреплику. Для обозначения дробных реплик, в которых
, то можно получить вторую полуреплику. Для обозначения дробных реплик, в которых 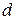 линейных эффектов приравнены к эффектам взаимодействия, пользуются условным обозначением
линейных эффектов приравнены к эффектам взаимодействия, пользуются условным обозначением 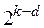 . Например, полуреплика от
. Например, полуреплика от 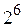 записывается в виде
записывается в виде 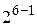 , а четверть-реплика -
, а четверть-реплика - 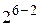 .
.
Если при имитационном эксперименте не исследуется взаимное влияние всех факторов целесообразно проводить частичный факторный эксперимент (ЧФЭ).
Наиболее часто используемыми планами ЧФЭ являются латинский план («латинский квадрат»), рандомизированный план и эксперимент с изменением факторов по одному.
Планы типа «латинского квадрата» используются в том случае, когда проводится эксперимент с одним первичным фактором и несколькими вторичными. Идея составления такого плана заключается в следующем. Если первичный фактор А имеет 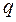 уровней, то для каждого вторичного фактора также выбирается
уровней, то для каждого вторичного фактора также выбирается 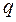 уровней, а выбор комбинаций уровней факторов производится в соответствии с правилом, которое рассмотрим на примере. Пусть в эксперименте используется первичный фактор А и два вторичных фактора В и С, имеющие каждый по
уровней, а выбор комбинаций уровней факторов производится в соответствии с правилом, которое рассмотрим на примере. Пусть в эксперименте используется первичный фактор А и два вторичных фактора В и С, имеющие каждый по 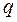 =4 уровней. План представляется в виде квадратной матрицы размером 4
=4 уровней. План представляется в виде квадратной матрицы размером 4 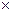 4 относительно уровней фактора А. Матрица строится таким образом, чтобы в каждой строке и в каждом столбце данный уровень фактора А встречался только один раз, как показано в таблице 16.1.
4 относительно уровней фактора А. Матрица строится таким образом, чтобы в каждой строке и в каждом столбце данный уровень фактора А встречался только один раз, как показано в таблице 16.1.
Т а б л и ц а 16.1
| Значение фактора В | Значение фактора С | |||
| С1 | С2 | С3 | С4 | |
| В1 | А1 | А2 | А3 | А4 |
| В2 | А2 | А3 | А4 | А1 |
| В3 | А3 | А4 | А1 | А2 |
| В4 | А4 | А1 | А2 | А3 |
Таким образом, количество прогонов необходимых для реализации плана составляет 4 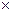 4=16, тогда как для аналогичного ПФЭ необходимо
4=16, тогда как для аналогичного ПФЭ необходимо 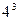 =64 прогона, а для ДФЭ – 32.
=64 прогона, а для ДФЭ – 32.
 Рандомизированный план предполагает выбор сочетания уровней случайным образом, причем начальным моментом в его реализации является число экспериментов, которое необходимо выполнить.
Рандомизированный план предполагает выбор сочетания уровней случайным образом, причем начальным моментом в его реализации является число экспериментов, которое необходимо выполнить.
Суть эксперимента с изменением факторов по одному заключается в том, что один из факторов изменяется по всем своим уровням, в то время как остальные фиксируются. Такой план требует 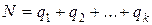 прогонов, что составит для рассматриваемого примера 12 прогонов.
прогонов, что составит для рассматриваемого примера 12 прогонов.
Еще раз подчеркнем, что использование ЧФЭ возможно только при отсутствии взаимодействия между факторами.
Итак, существуют два основных варианта постановки задачи планирования имитационного эксперимента:
1) из всех допустимых требуется выбрать такой план, который позволил бы получить наиболее достоверное значение функции реакции при фиксированном числе опытов;
2) из всех допустимых требуется выбрать такой план, при котором статистическая оценка функции реакции может быть получена с заданной точностью и достоверностью при минимальном объёме испытаний.
Решение задачи в первой постановке называют стратегическим планированием, во второй – тактическим планированием.
Рассмотрим возможности, предоставляемые MATLABом для планирования модельных экспериментов [36]. В состав библиотеки Statistics Toolbox (набор инструментов статистического анализа) входит 12 разделов.
В состав раздела Design of Experiments (планирование экспериментов) этой библиотеки входят функции, обеспечивающие разработку ПФЭ, ДФЭ и ЧФЭ.
 Для разработки ПФЭ предназначена функция fullfact, в качестве параметров которой указывается число уровней каждого, участвующего в моделировании, фактора. Данная функция записывается в командном окне MATLAB. Пусть, например, факторы А и В имеют по два уровня, а фактор С – три. Тогда обращение к функции будет иметь вид fullfact([2,2,3]). Записав его в командном окне и нажав ОК получим список всех возможных комбинаций уровней факторов, показанный на рис. 16.4. Список также сохраняется в рабочей области в переменной ans. Используя операцию индексирования можно поочередно вызывать оттуда строки плана. Так, введя команду ans(4,1:3), прочитаем в командном окне содержимое четвертой строки. Выполнив прогон модели для данного сочетания уровней факторов, строку можно удалить, используя редактор/отладчик MATLAB. Формирование плана ДФЭ осуществляется с помощью функции ff2n, параметром которой является число факторов. Результат ее выполнения представляет собой список возможных сочетаний уровней факторов, причем в списке значение 0 соответствует нижнему уровню, а 1 – верхнему. Так команда ff2n(3) выводит в командное окно список, показанный на рис. 16.5.
Для разработки ПФЭ предназначена функция fullfact, в качестве параметров которой указывается число уровней каждого, участвующего в моделировании, фактора. Данная функция записывается в командном окне MATLAB. Пусть, например, факторы А и В имеют по два уровня, а фактор С – три. Тогда обращение к функции будет иметь вид fullfact([2,2,3]). Записав его в командном окне и нажав ОК получим список всех возможных комбинаций уровней факторов, показанный на рис. 16.4. Список также сохраняется в рабочей области в переменной ans. Используя операцию индексирования можно поочередно вызывать оттуда строки плана. Так, введя команду ans(4,1:3), прочитаем в командном окне содержимое четвертой строки. Выполнив прогон модели для данного сочетания уровней факторов, строку можно удалить, используя редактор/отладчик MATLAB. Формирование плана ДФЭ осуществляется с помощью функции ff2n, параметром которой является число факторов. Результат ее выполнения представляет собой список возможных сочетаний уровней факторов, причем в списке значение 0 соответствует нижнему уровню, а 1 – верхнему. Так команда ff2n(3) выводит в командное окно список, показанный на рис. 16.5.
Говоря о методе планирования ЧФЭ, рассмотрим рандомизированный план. Для его получения используется функция unidrnd, представляющая собой датчик дискретной случайной величины, равномерно распределенной на заданном интервале, которая в общем случае используется с тремя параметрами и имеет вид unidrnd(N,k,m), где N – верхняя граница интервала распределения; а k и m задают число строк и столбцов генерируемой случайной матрицы. При создании ЧФЭ эти параметры интерпретируются как:
m – число факторов, каждый на N уровней;
k – выбранное экспериментатором число различных сочетаний уровней факторов.
Выполнение команды unidrnd(4,6,2) генерирует план ЧФЭ показанный на рис. 16.6.
 Наглядность процесса планирования экспериментов может быть повышена путём создания диалоговых окон, позволяющих выбрать вид эксперимента, число уровней факторов, способ использования плана эксперимента. Разработка таких окон выполняется с помощью компаненты Guide, которая вызывается из командного окна MATLAB командой File-Show GUI Layout Tool (файл-показать инструмент компановки интерфейса).
Наглядность процесса планирования экспериментов может быть повышена путём создания диалоговых окон, позволяющих выбрать вид эксперимента, число уровней факторов, способ использования плана эксперимента. Разработка таких окон выполняется с помощью компаненты Guide, которая вызывается из командного окна MATLAB командой File-Show GUI Layout Tool (файл-показать инструмент компановки интерфейса).
Тактическое планирование представляет собой определение способа проведения каждой серии испытаний машинной модели, предусмотренных планом эксперимента.
Тактическое планирование машинного эксперимента связано с решением следующих проблем:
1) определения начальных условий и их влияния на достижение установившегося результата при моделировании;
2) обеспечения точности и достоверности результатов моделирования;
3) уменьшения дисперсии оценок характеристик процесса функционирования моделируемых систем;
4) выбора правил автоматической остановки имитационного эксперимента с моделями систем.
Первая проблема возникает вследствие искусственного характера процесса функционирования модели 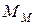 , которая в отличие от реальной системы
, которая в отличие от реальной системы 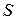 работает эпизодически, т. е. только, когда экспериментатор запускает машинную модель и проводит наблюдения. Поэтому всякий раз, когда начинается очередной прогон модели процесса функционирования системы
работает эпизодически, т. е. только, когда экспериментатор запускает машинную модель и проводит наблюдения. Поэтому всякий раз, когда начинается очередной прогон модели процесса функционирования системы 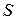 , требуется определенное время для достижения условий равновесия, которые соответствуют условиям функционирования реальной системы.
, требуется определенное время для достижения условий равновесия, которые соответствуют условиям функционирования реальной системы.
Начальный период работы машинной модели 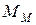 искажается из-за влияния начальных условий запуска модели. Для решения этой проблемы либо:
искажается из-за влияния начальных условий запуска модели. Для решения этой проблемы либо:
- исключается из рассмотрения информация о модели 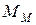 , полученная в начальной части периода моделирования (0, Т);
, полученная в начальной части периода моделирования (0, Т);
- начальные условия выбираются так, чтобы сократить время достижения установившегося режима.
На практике для снижения влияния переходного периода используют один из трёх методов:
1) повторения;
2) подинтервалов;
3) циклов.
В использовании метода повторений каждое наблюдение получается при помощи отдельного прогона модели, причём все прогоны начинаются при одних и тех же начальных условиях, но при этом используются различные последовательности моделей рабочей нагрузки, что позволяет получить статистически независимые наблюдения. Недостаток метода – в возможности сильного смещения наблюдений под влиянием начальных условий.
Метод подинтервалов основан на разбиении каждого прогона модели на равные промежутки времени, причём начало каждого интервала совпадает с началом очередного этапа наблюдений. Применение метода позволяет уменьшить влияние переходных условий со временем и наблюдения точнее отражают поведение системы в стационарном режиме. Однако, так как между интервалами существует автокорреляция, то значения наблюдаемых переменных полученные в начале очередного интервала зависят от конечных условий интервала предыдущего.
При использовании метода циклов влияние автокорреляции уменьшается за счёт выбора интервалов таким образом, чтобы в их начальных точках условия были одинаковыми.
Все эти приемы позволяют только уменьшить, но не свести к нулю время переходного процесса при проведении машинного эксперимента с моделью 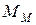 .
.
Решение второй проблемы (определение требуемой точности и достоверности) тактического планирования машинного эксперимента связано с оценкой точности и достоверности результатов моделирования при заданном числе реализаций (объеме выборки) или с необходимостью оценки необходимого числа реализаций при заданных точности и достоверности результатов моделирования системы 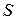 .
.
Обработка результатов имитационного эксперимента принципиально не может дать точных значений показателя эффективности 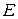 системы
системы 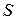 : в лучшем случае можно получить только некоторую оценку
: в лучшем случае можно получить только некоторую оценку 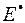 такого показателя. При этом экономические вопросы затрат людских и машинных ресурсов, обосновывающие целесообразность статистического моделирования вообще, оказываются тесно связанными с вопросами точности и достоверности оценки показателя эффективности
такого показателя. При этом экономические вопросы затрат людских и машинных ресурсов, обосновывающие целесообразность статистического моделирования вообще, оказываются тесно связанными с вопросами точности и достоверности оценки показателя эффективности 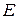 системы
системы 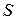 на ее модели
на ее модели 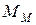 .
.
Таким образом, количество реализаций 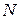 при статистическом моделировании системы
при статистическом моделировании системы 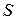 должно выбираться исходя из двух основных соображений: определения затрат ресурсов на машинный эксперимент с моделью
должно выбираться исходя из двух основных соображений: определения затрат ресурсов на машинный эксперимент с моделью 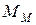 (включая построение модели и ее машинную реализацию) и оценки точности и достоверности результатов эксперимента с моделью системы
(включая построение модели и ее машинную реализацию) и оценки точности и достоверности результатов эксперимента с моделью системы 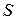 (при заданных ограничениях на ресурсы). Очевидно, что требования получения более хороших оценок и сокращения затрат ресурсов являются противоречивыми и при планировании машинных экспериментов на базе статистического моделирования необходимо решить задачу нахождения разумного компромисса между ними.
(при заданных ограничениях на ресурсы). Очевидно, что требования получения более хороших оценок и сокращения затрат ресурсов являются противоречивыми и при планировании машинных экспериментов на базе статистического моделирования необходимо решить задачу нахождения разумного компромисса между ними.
Из-за наличия стохастичности и ограниченности числа реализаций 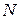 в общем случае
в общем случае 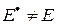 .
.
Разность между ними называется точностью (абсолютной) оценки;
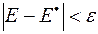
вероятность того, что неравенство выполняется, называется достоверностью оценки
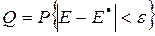
Величина 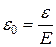
 называется относительной точностью оценки, а достоверность оценки соответственно будет иметь вид
называется относительной точностью оценки, а достоверность оценки соответственно будет иметь вид
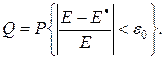
Для того чтобы при статистическом моделировании системы 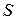 по заданным
по заданным 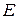 и
и 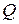 определить количество реализаций
определить количество реализаций 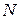 или, наоборот, при ограниченных ресурсах (известном
или, наоборот, при ограниченных ресурсах (известном 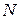 ) найти необходимые
) найти необходимые 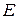 и
и 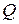 , следует детально изучить соотношение для достоверности. Сделать это удается не во всех случаях, так как закон распределения вероятностей величины
, следует детально изучить соотношение для достоверности. Сделать это удается не во всех случаях, так как закон распределения вероятностей величины 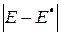 для многих практических случаев исследования систем установить не удается либо в силу ограниченности априорных сведений о системе
для многих практических случаев исследования систем установить не удается либо в силу ограниченности априорных сведений о системе 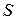 , либо из-за сложности вероятностных расчетов.
, либо из-за сложности вероятностных расчетов.
Рассмотрим взаимосвязь точности и достоверности результатов с количеством реализаций при машинном эксперименте, когда в качестве показателей эффективности 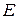 выступают вероятность
выступают вероятность 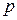 ,математическое ожидание
,математическое ожидание 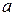 и дисперсия
и дисперсия 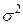 .
.
Пусть цель машинного эксперимента с моделью 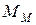 некоторой системы
некоторой системы 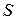 — получение оценки
— получение оценки 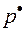 вероятности появления
вероятности появления 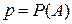 некоторого события
некоторого события 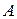 , определяемого состояниями процесса функционирования исследуемой системы
, определяемого состояниями процесса функционирования исследуемой системы 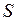 .
.
В качестве оценки вероятности 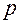 в данном случае выступает частность
в данном случае выступает частность 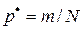 , где
, где 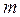 — число положительных исходов.
— число положительных исходов.
Тогда соотношение, связывающее точность и достоверность оценок с количеством реализаций, будет иметь вид
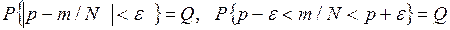
Для ответа на вопрос о законе распределения величины 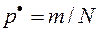 представим эту частость в виде
представим эту частость в виде 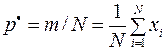 .
.
Так как количество наступлений события 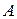 является случайной величиной, принимающей значения
является случайной величиной, принимающей значения 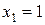 с вероятностью
с вероятностью 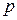 и
и 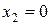 с дополнительной вероятностью
с дополнительной вероятностью 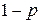 , то математическое ожидание и дисперсия этой случайной величины будут:
, то математическое ожидание и дисперсия этой случайной величины будут:
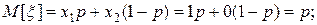
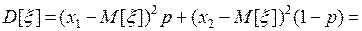
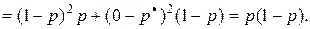
Тогда
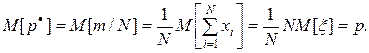
Это соотношение говорит о несмещенности оценки 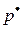 для вероятности
для вероятности 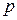 .
.
С учетом независимости значений величин 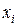 , получим
, получим
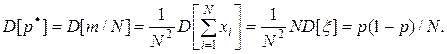
В силу предельной теоремы теории вероятностей (или ее частного случая—теоремы Лапласа) частость 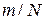 при достаточно больших
при достаточно больших 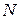 можно рассматривать как случайную величину, описываемую нормальным законом распределения вероятностей с математическим ожиданием
можно рассматривать как случайную величину, описываемую нормальным законом распределения вероятностей с математическим ожиданием 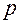 и дисперсией
и дисперсией 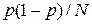 . Поэтому соотношение, связывающее точность и достоверность с количеством реализаций можно переписать так:
. Поэтому соотношение, связывающее точность и достоверность с количеством реализаций можно переписать так:
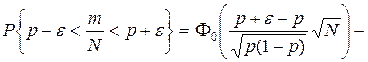
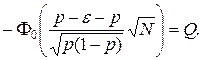
Учитывая, что 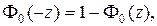 получим
получим
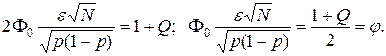
Тогда
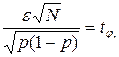
где 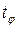 – квантиль нормального распределения вероятностей порядка
– квантиль нормального распределения вероятностей порядка 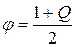 , находится из специальных таблиц.
, находится из специальных таблиц.
В результате точность оценки 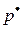 вероятности
вероятности 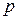 можно определить как
можно определить как
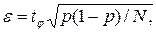
т. е. точность оценки вероятностей обратно пропорционально 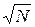 .
.
Из соотношения для точности оценки 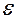 можно вычислить количество реализаций
можно вычислить количество реализаций
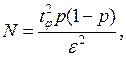
необходимых для получения оценки 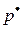 с точностью
с точностью 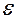 и достоверностью
и достоверностью 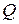 .
.
Для математического ожидания 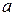 точность оценки
точность оценки 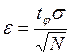 , а количество реализаций
, а количество реализаций
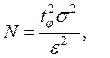 или
или 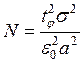 .
.
Если в качестве показателя эффективности 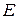 системы
системы 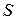 выступает дисперсия
выступает дисперсия 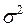 , а в качестве ее оценки используется величина
, а в качестве ее оценки используется величина 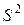 , то математическое ожидание и дисперсия соответственно будут
, то математическое ожидание и дисперсия соответственно будут
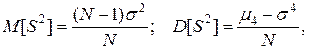
где 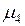 — центральный момент четвертого порядка случайной величины.
— центральный момент четвертого порядка случайной величины.
Для дисперсии 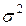 точность оценки
точность оценки 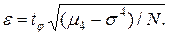
Отсюда количество реализаций будет
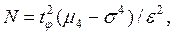 или
или 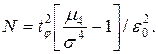
Для частного случая, когда случайная величина имеет нормальное распределение 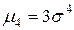 , получим
, получим 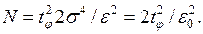
Проблема уменьшения дисперсии оценок характеристик процесса функционирования моделируемых систем.
Таким образом, с проблемой выбора количества реализаций при обеспечении необходимой точности и достоверности результатов машинного эксперимента тесно связана и третья проблема, а именно проблема уменьшения дисперсии. В настоящее время существуют методы, позволяющие при заданном числе реализации увеличить точность оценок, полученных на машинной модели 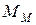 , и, наоборот, при заданной точности оценок сократить необходимое число реализации при статистическом моделировании. Эти методы используют априорную информацию о структуре и поведении моделируемой системы
, и, наоборот, при заданной точности оценок сократить необходимое число реализации при статистическом моделировании. Эти методы используют априорную информацию о структуре и поведении моделируемой системы 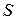 и называются методами понижения дисперсии.
и называются методами понижения дисперсии.
Рассмотрим в качестве иллюстрации метод коррелированных реализаций (выборок), используемый в задачах сравнения двух или более альтернатив. При исследовании и проектировании системы 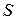 всегда происходит сравнение вариантов
всегда происходит сравнение вариантов 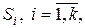 отличающихся друг от друга структурой, алгоритмами поведения и параметрами.
отличающихся друг от друга структурой, алгоритмами поведения и параметрами.
Независимо от того, как организуется выбор наилучшего варианта системы 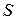 (простым перебором результатов моделирования системы
(простым перебором результатов моделирования системы 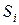 или с помощью автоматизированной процедуры поиска), элементарной операцией при этом является сравнение статистически усредненных критериев интерпретации.
или с помощью автоматизированной процедуры поиска), элементарной операцией при этом является сравнение статистически усредненных критериев интерпретации.
Сравниваемые статистические показатели 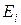 вариантов моделируемой системы
вариантов моделируемой системы 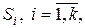 полученные на машинной модели
полученные на машинной модели 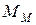 ,можно записать в виде средних значений
,можно записать в виде средних значений 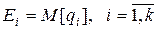 критериев
критериев 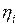 , характеризующих систему
, характеризующих систему 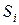 , или в виде средних значений функций этих критериев
, или в виде средних значений функций этих критериев 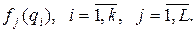 Например, если
Например, если
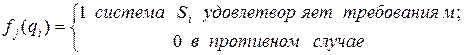
то показатели 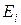 являются вероятностями нормальной работы системы
являются вероятностями нормальной работы системы 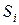 . Если
. Если
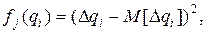
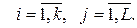
то показатель 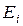 является дисперсией значения контролируемой величины и т. д. Здесь
является дисперсией значения контролируемой величины и т. д. Здесь 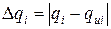 — отклонение значения контролируемой для системы
— отклонение значения контролируемой для системы 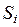 , величины
, величины 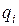 от истинной
от истинной 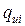 .
.
В дальнейшем, поскольку при сравнении характеристик, полученных на машинной модели 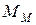 , всегда рассматриваются два конкурирующих варианта моделируемой системы, будем сопоставлять только две системы:
, всегда рассматриваются два конкурирующих варианта моделируемой системы, будем сопоставлять только две системы: 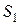 и
и 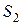 . Существенной особенностью операции сравнения вариантов систем
. Существенной особенностью операции сравнения вариантов систем 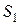 и
и 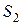 является повышение требований к точности статистических оценок
является повышение требований к точности статистических оценок 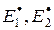 показателей
показателей 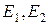 при уменьшении разности
при уменьшении разности 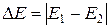 . Это обстоятельство требует разработки специальных приемов получения статистически зависимых оценок для уменьшения дисперсии.
. Это обстоятельство требует разработки специальных приемов получения статистически зависимых оценок для уменьшения дисперсии.
Рассмотрим наиболее характерные случаи, имеющие место при имитационных экспериментах, когда в качестве оценок выступают средние значения, вероятности и дисперсии [34].
Если полученные в результате имитационного эксперимента с вариантами модели системы 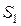 и
и 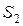 оценки
оценки 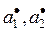 средних значений критериев
средних значений критериев 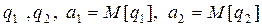 имеют дисперсии
имеют дисперсии 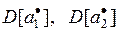 и коэффициент корреляции оценок
и коэффициент корреляции оценок 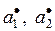 равен
равен 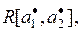 тодисперсию погрешности оценки
тодисперсию погрешности оценки 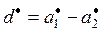 разности
разности 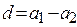 можно найти из соотношения
можно найти из соотношения
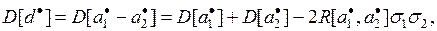
где 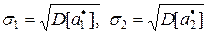 – средние квадратические отклонения оценок.
– средние квадратические отклонения оценок.
При независимом моделировании вариантов системы с использованием различных реализаций псевдослучайных последовательностей коэффициент корреляции оценок 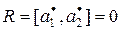 и
и 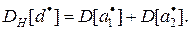
При моделировании удается получить положительный коэффициент корреляции 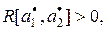 т. е.
т. е. 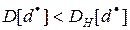 , когда при имитационных экспериментах с вариантами системы
, когда при имитационных экспериментах с вариантами системы 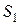 и
и 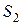 используются, например, одни и те же псевдослучайные последовательности. Рассмотренные соотношения для дисперсии
используются, например, одни и те же псевдослучайные последовательности. Рассмотренные соотношения для дисперсии 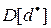 не связаны со специальными предположениями о способе получения оценок
не связаны со специальными предположениями о способе получения оценок 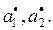
Пример. Рассмотрим полученные при машинном моделировании реализации 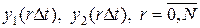 критериев
критериев 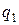 и
и 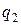 как выборку из двухмерного векторного стационарного процесса
как выборку из двухмерного векторного стационарного процесса 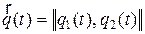 со средним значением
со средним значением 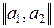 и матричной корреляционной функцией
и матричной корреляционной функцией
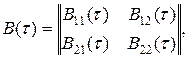
где 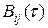 — автокорреляционная функция,
— автокорреляционная функция,
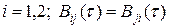 — взаимная корреляционная функция компонентов
— взаимная корреляционная функция компонентов 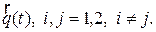
Тогда можно показать, что
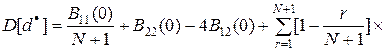
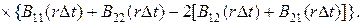
Эту формулу применяют для расчета точности оценки 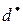 при заданной матричной корреляционной функции
при заданной матричной корреляционной функции 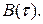
Вероятности 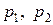 событий
событий 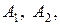 характеризующих сравниваемые варианты модели систем
характеризующих сравниваемые варианты модели систем 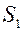 и
и 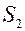 , можно представить как средние значения двоичных случайных величин
, можно представить как средние значения двоичных случайных величин 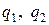 с распределением вероятностей
с распределением вероятностей 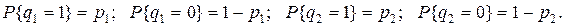
Поэтому для оценки разности вероятностей 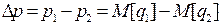 можно использовать все выражения, полученные ранее при сравнении средних значений, видоизменив в них обозначения с учетом того, что двухмерное распределение вектора
можно использовать все выражения, полученные ранее при сравнении средних значений, видоизменив в них обозначения с учетом того, что двухмерное распределение вектора 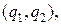 описывающее зависимость между событиями
описывающее зависимость между событиями 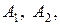 имеет вид
имеет вид
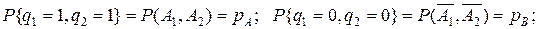
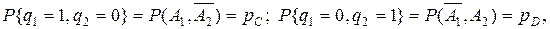
причем 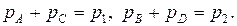 В частности, для повторной выборки объемом
В частности, для повторной выборки объемом 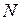 получим, что оценка
получим, что оценка
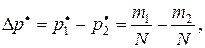
где 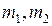 —количество наступлений событий
—количество наступлений событий 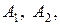 полученных при независимых прогонах модели. Учитывая, что между
полученных при независимых прогонах модели. Учитывая, что между 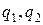 ковариация
ковариация 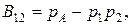 найдем дисперсию оценки
найдем дисперсию оценки
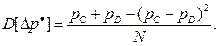
Если в процессе проведения имитационных экспериментов с моделью фиксируются эмпирические частоты 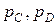 событий
событий 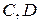 , то для дисперсии
, то для дисперсии 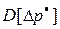 при достаточно большом
при достаточно большом 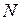 можно воспользоваться несмещенной оценкой
можно воспользоваться несмещенной оценкой
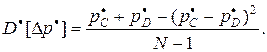
И, наконец, рассмотрим случай, когда в качестве оценки вариантов систем 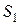 и
и 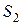 выступает дисперсия. В этом случае оценка
выступает дисперсия. В этом случае оценка 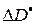 разности
разности 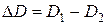 дисперсий критериев
дисперсий критериев 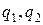 вычисляется по независимым реализациям вектора
вычисляется по независимым реализациям вектора 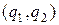 с помощью формулы
с помощью формулы 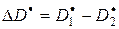 , где
, где
