Ковариация
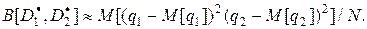
Пример. Пусть сравниваемые критерии 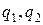 имеют нормальное распределение
имеют нормальное распределение
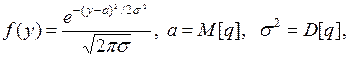
тогда
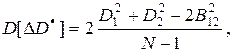
где 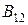 — ковариация. Использование зависимых испытаний дает выигрыш в точности сравнения дисперсий
— ковариация. Использование зависимых испытаний дает выигрыш в точности сравнения дисперсий 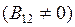 независимо от знака корреляции. Воспользовавшись оценкой
независимо от знака корреляции. Воспользовавшись оценкой
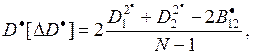
можно организовать последовательную процедуру сравнения дисперсий для вариантов системы 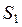 и
и 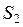 .
.
Таким образом, при таком подходе к уменьшению дисперсии задача состоит в специальном построении моделирующего алгоритма системы 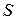 , позволяющего получить положительную корреляцию, например, за счет управления генерацией случайных величин. Вопрос об эффективности использования метода уменьшения дисперсии может быть решен только с учетом необходимости дополнительных затрат машинных ресурсов (времени и памяти) на реализацию подхода, т. е. теоретическое уменьшение затрат машинного времени на моделирование вариантов системы (при той же точности результатов) должно быть проверено на сложность машинной реализации модели.
, позволяющего получить положительную корреляцию, например, за счет управления генерацией случайных величин. Вопрос об эффективности использования метода уменьшения дисперсии может быть решен только с учетом необходимости дополнительных затрат машинных ресурсов (времени и памяти) на реализацию подхода, т. е. теоретическое уменьшение затрат машинного времени на моделирование вариантов системы (при той же точности результатов) должно быть проверено на сложность машинной реализации модели.
Проблема выбора правил автоматической остановки имитационного эксперимента с моделями системы.
Простейший способ решения проблемы — задание требуемого количества реализации 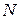 (или длины интервала моделирования
(или длины интервала моделирования 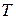 ).
).
Другой способ — задание доверительных интервалов для выходных переменных и остановка прогона машинной модели 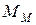 при достижении заданного доверительного интервала, что позволяет теоретически приблизить время прогона к оптимальному. При практической реализации введение в модель
при достижении заданного доверительного интервала, что позволяет теоретически приблизить время прогона к оптимальному. При практической реализации введение в модель 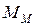 правил остановки и операций вычисления доверительных интервалов увеличивает машинное время, необходимое для получения одной выборочной точки при статистическом моделировании.
правил остановки и операций вычисления доверительных интервалов увеличивает машинное время, необходимое для получения одной выборочной точки при статистическом моделировании.
Правила автоматической остановки могут быть включены в машинную модель такими способами:
1) путем двухэтапного проведения прогона, когда сначала делается пробный прогон из 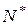 реализаций, позволяющий оценить необходимое количество реализации
реализаций, позволяющий оценить необходимое количество реализации 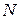 (причем, если
(причем, если 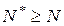 , то прогон можно закончить, а в противном случае необходимо набрать еще
, то прогон можно закончить, а в противном случае необходимо набрать еще 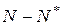 реализаций);
реализаций);
2) путем использования последовательного анализа для определения минимально необходимого количества реализации 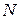 , которое рассматривается при этом как случайная величина, зависящая от результатов
, которое рассматривается при этом как случайная величина, зависящая от результатов 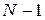 предыдущих реализаций (наблюдений, испытаний) машинного эксперимента.
предыдущих реализаций (наблюдений, испытаний) машинного эксперимента.
Рассмотрим особенности последовательного планирования машинных экспериментов, построенных на последовательном анализе. В последовательном анализе объем выборки не фиксирован, а после i-ro наблюдения принимается одно из следующих решений: принять данную гипотезу, отвергнуть гипотезу, продолжить испытания, т. е. повторить наблюдения еще раз. Благодаря такому подходу можно объем выборки существенно уменьшить по сравнению со способами остановки, использующими фиксированный объем выборки. Таким образом, последовательное планирование машинного эксперимента позволяет минимизировать объем выборки в эксперименте, необходимой для получения требуемой при исследовании системы 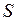 информации. Построив критерий, можно на каждом шаге решать вопрос либо о принятии нулевой гипотезы
информации. Построив критерий, можно на каждом шаге решать вопрос либо о принятии нулевой гипотезы 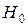 , либо о принятии альтернативной гипотезы
, либо о принятии альтернативной гипотезы 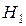 , либо о продолжении машинного эксперимента. Последовательное планирование машинного эксперимента использует принцип максимального правдоподобия и последовательные проверки статистических гипотез.
, либо о продолжении машинного эксперимента. Последовательное планирование машинного эксперимента использует принцип максимального правдоподобия и последовательные проверки статистических гипотез.
Пусть распределение генеральной совокупности характеризуется функцией плотности вероятностей с неизвестным параметром 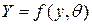 . Определяются нулевая и альтернативная гипотезы
. Определяются нулевая и альтернативная гипотезы 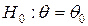 и
и 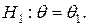 Гипотезы проверяют на основании выборки нарастающего объема
Гипотезы проверяют на основании выборки нарастающего объема 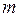 . Можно записать: вероятность получения данной выборки
. Можно записать: вероятность получения данной выборки 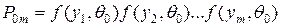 при условии, что верна гипотеза
при условии, что верна гипотеза 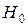 (правдоподобная выборка); вероятность получения выборки
(правдоподобная выборка); вероятность получения выборки 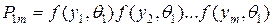 при условии верности гипотезы
при условии верности гипотезы 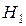 . Процедура проверки строится на отношении правдоподобия
. Процедура проверки строится на отношении правдоподобия 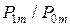 .
.
Последовательный критерий отношения вероятностей строится следующим образом. На каждом шаге машинного эксперимента определяются 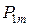 и
и 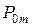 , а также проверяется условие: если
, а также проверяется условие: если 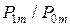
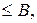 то принимается
то принимается 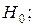 если
если 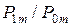 <A или >B, то эксперимент продолжается и, наконец, если
<A или >B, то эксперимент продолжается и, наконец, если 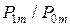
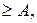 то принимается
то принимается 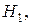 где
где 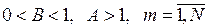 .
.
Для сходимости критерия необходимо, чтобы 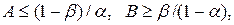 где
где 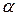 —вероятность ошибки первого рода;
—вероятность ошибки первого рода; 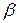 —вероятность ошибки второго рода.
—вероятность ошибки второго рода.
Данный метод позволяет снизить среднее число реализаций в машинных экспериментах по сравнению с использованием фиксированных объемов выборки (при одинаковых вероятностях ошибок). Примером применения метода может служить проверка гипотезы о среднем значении величины, распределенной по нормальному закону.
Пример. Пусть для случайной величины 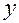 известна дисперсия
известна дисперсия 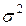 и неизвестно среднее
и неизвестно среднее 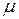 . При этом нулевая гипотеза
. При этом нулевая гипотеза 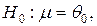 альтернативная
альтернативная 
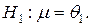 Если
Если 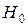 верна, то вероятность ее отвергнуть равна
верна, то вероятность ее отвергнуть равна 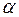 . Если верна гипотеза
. Если верна гипотеза 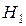 , то вероятность принять ее равна
, то вероятность принять ее равна 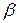 . В случае
. В случае 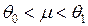 ни одна из гипотез не принимается.
ни одна из гипотез не принимается.
Для нормального распределения
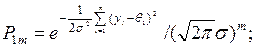
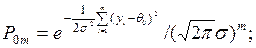
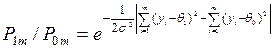
Критерий проверки гипотезы строится по следующему правилу: если
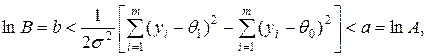
то наблюдение продолжается.
Для математического ожидания числа наблюдений при условии верности 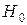 и
и 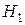 соответственно можно записать
соответственно можно записать
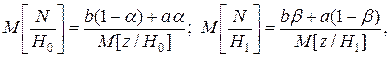
где 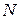 —число наблюдений;
—число наблюдений;
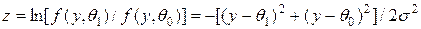 .
.
Можно записать 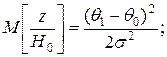
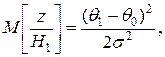 так как
так как 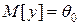 для гипотезы
для гипотезы 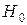 и
и 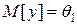 для гипотезы
для гипотезы 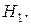
Тогда
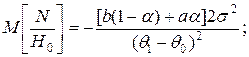
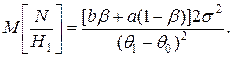
Применение данного метода по сравнению с фиксированным объемом выборки 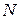 дает уменьшение числа реализаций при статистическом моделировании более чем в два раза.
дает уменьшение числа реализаций при статистическом моделировании более чем в два раза.
Для проверки гипотезы о среднем для случайных величин с нормальным законом распределения, неизвестным средним 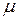 и неизвестной дисперсией
и неизвестной дисперсией 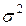 можно использовать следующую процедуру. Проверяют гипотезы
можно использовать следующую процедуру. Проверяют гипотезы 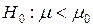 и
и 
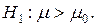 Необходимо, чтобы вероятность отвергнуть
Необходимо, чтобы вероятность отвергнуть 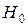 при
при 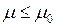 была
была 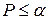 и вероятность принять
и вероятность принять 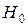 при
при 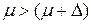 была
была 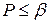 .
.
На первом шаге берут выборку размером 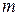 и вычисляют выборочную дисперсию
и вычисляют выборочную дисперсию
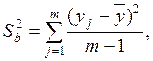
где число 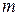 выбрано таким, чтобы выполнялось условие
выбрано таким, чтобы выполнялось условие
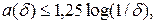
где 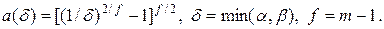
Затем последовательно проводят по одному эксперименту. При выполнении условия
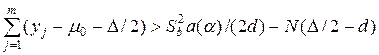
эксперимент прекращают и гипотезу 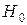 отвергают.
отвергают.
Гипотезу 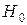 принимают, если
принимают, если
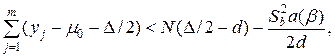
где 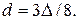
Таким образом, чем сложнее машинная модель 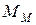 , тем важнее этап тактического планирования машинного эксперимента, выполняемый непосредственно перед моделированием на ЭВМ системы
, тем важнее этап тактического планирования машинного эксперимента, выполняемый непосредственно перед моделированием на ЭВМ системы 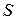 . Процесс планирования машинных экспериментов с моделью
. Процесс планирования машинных экспериментов с моделью 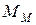 итерационен, т. е. при уточнении некоторых свойств моделируемой системы
итерационен, т. е. при уточнении некоторых свойств моделируемой системы 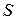 этапы стратегического и тактического планирования экспериментов могут чередоваться.
этапы стратегического и тактического планирования экспериментов могут чередоваться.
Контрольные вопросы и задачи
16.1. Какая цель ставиться перед стратегическим планированием модельного эксперимента?
16.2. Какая цель ставиться перед тактическим планированием модельного эксперимента?
16.3. Что такое стохастическая сходимость и каковы пути её ускорения?
16.4. Какие проблемы решаются при тактическом планировании машинно-модельного эксперимента?
16.5. Из каких соображений должно выбираться количество реализаций 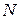 при одном прогоне имитационной модели?
при одном прогоне имитационной модели?
16.6. Какие функции в MATLAB используются для планирования модельного эксперимента?
Дата добавления: 2015-10-13; просмотров: 1006;
