Пример 3.3.
Имеются следующие данные:
Таблица 3.2.
| Группы рабочих по количеству произведенной продукции за смену, шт. | Число рабочих, ni | Середина интервала, хi | хini |
| 3 – 5 | |||
| 5 – 7 | |||
| 7 – 9 | |||
| 9 – 11 | |||
| 11 – 13 | |||
| ИТОГО |
Исчислим среднюю выработку продукции одним рабочим за смену. В данном ряду варианты осредняемого признака (продукции за смену) представлены не одним числом, а в виде интервала «от – до». Рабочие первой группы производят продукцию от 3 до 5 шт., рабочие второй группы – от 5 до 7 шт. и т.д. Таким образом, каждая группа ряда распределения имеет нижнее и верхнее значения вариант, или закрытые интервалы. Исчисление средней по сгруппированным данным производится по формуле средней арифметической взвешенной:
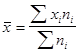
Чтобы применить эту формулу, необходимо варианты признака выразить одним числом (дискретным). За такое дискретное число принимается средняя арифметическая простая из верхнего и нижнего значения интервала. Так, для первой группы дискретная величина х будет равна: (3+5) / 2 =4
Дальнейший расчет производится обычным методом определения средней арифметической взвешенной: 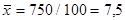 .
.
Итак, все рабочие произвели 750 шт. изделий за смену, а каждый в среднем произвел 7,5 шт.
Преобразуем рассмотренный выше ряд распределения в ряд с открытыми интервалами.
Дата добавления: 2015-09-02; просмотров: 595;
