Пример 3.2.
Имеются следующие данные о заработной плате рабочих – сдельщиков:
Таблица 3.1.
Месячная з/п
(варианта – 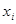 ), тыс. руб. ), тыс. руб.
| Число рабочих, 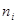
| хini |
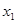 = 1,1 = 1,1
| 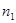 = 2 = 2
| 2,2 |
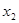 = 1,3 = 1,3
| 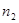 = 6 = 6
| 7,8 |
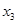 = 16, = 16,
| 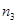 = 16 = 16
| 25,6 |
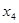 = 1,9 = 1,9
| 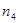 = 12 = 12
| 22,8 |
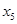 = 2,2 = 2,2
| 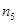 = 14 = 14
| 30,8 |
| ИТОГО | 89,2 |
По данным дискретного ряда распределения видно, что одни и те же значения признака (варианты) повторяются несколько раз. Так, варианта х1 встречается в совокупности 2 раза, а варианта х3-16 раз и т.д.
Число одинаковых значений признака в рядах распределения называется частотой или весом и обозначается символом n.
Вычислим среднюю заработную плату одного рабочего 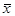 в тыс. руб.:
в тыс. руб.:
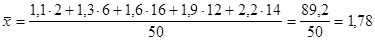
Фонд заработной платы по каждой группе рабочих равен произведению варианты на частоту, а сумма этих произведений дает общий фонд заработной платы всех рабочих.
В соответствии с этим расчеты можно представить в общем виде:
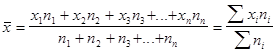
Полученная формула называется средней арифметической взвешенной.
Из нее видно, что средняя зависит не только от значений признака, но и от их частот, т.е. от состава совокупности, от ее структуры. Изменим в условии задачи состав рабочих и исчислим среднюю в измененной структуре.
Статистический материал в результате обработки может быть представлен не только в виде дискретных рядов распределения, но и в виде интервальных вариационных рядов с закрытыми или открытыми интервалами.
Рассмотрим расчет средней арифметической для таких рядов.
Дата добавления: 2015-09-02; просмотров: 637;
