Решаем задачу по методу максимального элемента.
Составляем опорный план (табл. 2)
Табл.2
| Bj Ai | П1 | П2 | П3 | П4 | П5 | Ui | |||
| СО-1 | 3 | 59 7 | 2 | 11 – W | +W | U1=-1 | |||
| 5 | 0 | ||||||||
| СО-2 | 18 -W | 49 | 32 | +W 6 | 0 | U2= 0 | |||
| 2 | 3 | 4 | |||||||
| СО-3 | 29 | +W | 51 | -W | U3 =4 | ||||
| 6 | 4 | 3 | 5 | 0 | |||||
| Vj | V1=2 | V2=8 | V3=4 | V4=6 | V5= -4 | W=11 |
Проверяем на вырожденность.
Z= m+n-1=3+5-1=7
Базисных клеток 7. План не вырожден.
Проверяем опорный план на оптимальность.
Задаем U2 = 0 и определяем значения потенциалов.
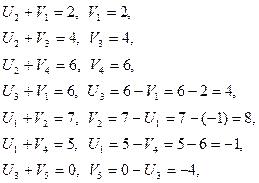
Вычисляем оценки для всех незаполненных клеток (Dij)
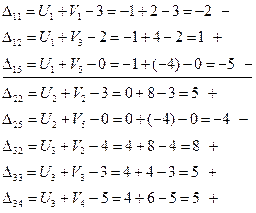
Опорное решение не является оптимальным, так как имеются отрицательные оценки.
Переходим к следующему плану.
Для клетки (1,5) с наименьшей оценкой (-5) строим цикл. Ставим в эту клетку коэффициент W со знаком «+» и применяя метод наибольшего элемента находим цикл, (табл. 2). Определяем из цикла W =11
Осуществляем сдвиг по циклу и строим следующий план (табл. 3)
.
Табл.3
| Bj Ai | П1 | П2 | П3 | П4 | П5 | Ui | |||
| СО-1 | 3 | 59 7 | 2 | 11 | U1=4 | ||||
| 5 | 0 | ||||||||
| СО-2 | 7 -W | 49 | 43 | +W | U2= 0 | ||||
| 2 | 3 | 4 | 6 | 0 | |||||
| СО-3 | 40 | +W | 40 | -W | U3 =4 | ||||
| 6 | 4 | 3 | 5 | 0 | |||||
| Vj | V1=2 | V2=3 | V3=4 | V4=6 | V5= -4 |
Проверяем план на оптимальность методом максимального элемента, как в п.З.
Задаем U2 = 0 и определяем значения потенциалов.
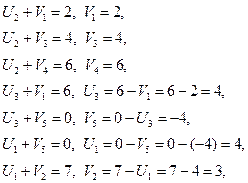
Вычисляем оценки для всех незаполненных клеток (Dij)
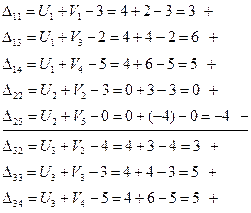
Определяем из циклаW=7
Осуществляем сдвиг по циклу и строим следующий план (табл. 4).
Табл. 4
| Bj Ai | П1 | П2 | П3 | П4 | П5 | Ui | |
| СО-1 | 3 | 59 7 | 2 | 11 | U1=0 | ||
| 5 | 0 | ||||||
| СО-2 | 2 | 3 | 49 4 | 43 6 | 7 0 | U2= 0 | |
| СО-3 | 47 6 | 4 | 3 | 5 | 33 0 | U3 =0 | |
| Vj | V1=6 | V2=7 | V3=4 | V4=6 | V5= 0 |
Проверяем план на оптимальность методом максимального
элемента, как в п.З.
Задаем U2 = 0 и определяем значения потенциалов.
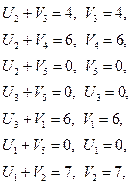
Вычисляем оценки для всех незаполненных клеток (Dij)
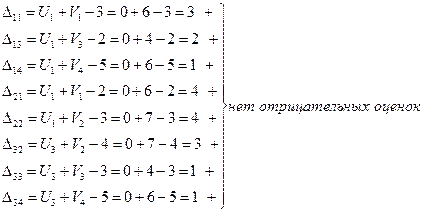
план табл. 4 оптимален.
Определяем значение целевой функции прямойидвойственной задачи:
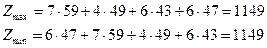
Исходя из первой теоремы двойственности в условии нашей задачи Zmax=Zmin=1149 (Z=Z’) последний план оптимален
Ответ:
1) Чтобы за рабочий день было убрано максимально возможное количество картофеля, следует распределить студентов по полям следующим образом:
– Из СО-1 выделить 59 человек для уборки картофеля на втором поле П2, а 11 человек останутся в СО;
– из СО-2 выделить 49 человек для уборки картофеля на ПЗ и 43 человека для уборки картофеля на П4, а 7 человек останутся в СО;
– из СО-3 выделить 47 человек для уборки картофеля на П1, а 33 человека оставить в СО.
2) При данном оптимальном распределении студентов с четырех полей будет убрано 1149 центнеров картофеля.
Пример № 2
План перевозок:
| Поставщики Аi | Потребители Вj: | |||||
| Запасы аi | Себестоимость | В1 | В2 | В3 | В4 | |
| А1 | ||||||
| А2 | ||||||
| А3 |
Решение:
Проверяем на сбалансированность
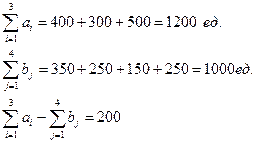
Задача не сбалансированная. Введем фиктивного потребителя В5 с потребностью в грузе, равной 200 ед. Стоимость перевозки для фиктивного потребителя определим равной нулю.
В качестве общей стоимости будем брать сумму затрат на доставку единицы продукции из соответствующего пункта и ее себестоимость в этом пункте.
Дата добавления: 2015-10-13; просмотров: 969;
