Общая постановка задачи

Линейное программирование — наука о ме­тодах исследования и отыскания экстремальных (наибольших и наименьших) значений линейной функции, на неизвестные которой наложены линейные ограничения.

Эта линейная функция называется целевой, а ограничения, которые математически записываются в виде уравнений или неравенств, называются системой ограничений.

Определение.

Математическое выражение целевой функ­ции и ее ограничений называется математической моделью экономической задачи.

В общем виде математическая модель задачи линейного программирования (ЛП) записывается как

Z(x)=C₁X₁+C₂X₂ + ^{. . .} +С_JX_J + ^{. . .} +С_nX_{n _} max(min)

при ограничениях:

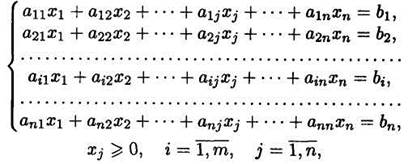
где X_i — неизвестные;a _ij , b_j , C_i — заданные постоянные вели­чины.

Все или некоторые уравнения системы ограничений могут быть записаны в виде неравенств.

Математическая модель в более краткой записи имеет вид

Z(x) = ∑C_i X_i max(min)

при ограничениях:

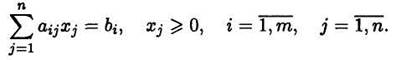
ОпределениеДопустимым решением (планом) зада­чи линейного программирования называется вектор X = (х₁, х₂, ,...х_n , ) , удовлетворяющий системе ограничений.

Множество допустимых решений образует область допус­тимых решений (ОДР).

ОпределениеДопустимое решение, при котором целевая функция достигает своего экстремального значения, называ­ется оптимальным решением задачи линейного программиро­вания и обозначается Х_опт.

Базисное допустимое решение

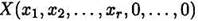
Является опорным решением, где r— ранг системы ограничений.