Свойства сходящихся рядов
Лекция №7
Основные понятия сходимости числовых рядов.
Числовым рядом называется выражение вида 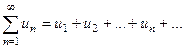 , где
, где 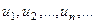 являются членами числового ряда и представляют собой действительные или комплексные числа.
являются членами числового ряда и представляют собой действительные или комплексные числа.
Числовой ряд задается с помощью формулы общего члена ряда 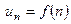 , описывающей зависимость члена ряда от его номера.
, описывающей зависимость члена ряда от его номера.
Пример 1.Найти общий член ряда 
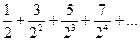 .
.
Решение. Последовательные числители образуют арифметическую прогрессии. 1,3,5,7,…;  й член прогрессии находим по формуле
й член прогрессии находим по формуле 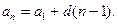 Здесь
Здесь 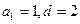 , поэтому
, поэтому 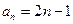 . Последовательные знаменатели образуют геометрическую прогрессии.
. Последовательные знаменатели образуют геометрическую прогрессии. 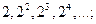
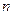 -й член этой прогрессии
-й член этой прогрессии 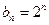 . Следовательно, общий член ряда
. Следовательно, общий член ряда 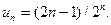
Пример 2. Найти общий член ряда 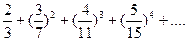
Решение. Показатель степени каждого члена совпадает с номером этого члена, поэтому показатель степени  го члена равен
го члена равен 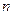 . Числители дробей 2/3,3/7,4/11,5/15,… образуют арифметическую прогрессию с первым членом 2 и разностью 1. Поэтому
. Числители дробей 2/3,3/7,4/11,5/15,… образуют арифметическую прогрессию с первым членом 2 и разностью 1. Поэтому 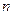 -й числитель равен
-й числитель равен 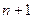 . Знаменатели образуют арифметическую прогрессию с первым членом 4 и разностью 4. Следовательно,
. Знаменатели образуют арифметическую прогрессию с первым членом 4 и разностью 4. Следовательно, 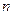 -й знаменатель равен
-й знаменатель равен 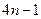 . Итак, общим членом ряда является
. Итак, общим членом ряда является 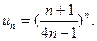
Сумма 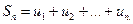 первых
первых 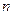 членов ряда называется
членов ряда называется 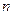 -й частичной суммойряда. Рассмотрим последовательность частичных сумм числового ряда:
-й частичной суммойряда. Рассмотрим последовательность частичных сумм числового ряда:
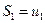 ,
, 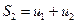 ,
,  , …
, …
Определение. Если существует конечный предел 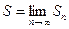 последовательности частичных сумм ряда, то говорят, что числовой ряд сходится. Этот предел называют суммой ряда
последовательности частичных сумм ряда, то говорят, что числовой ряд сходится. Этот предел называют суммой ряда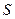 .
.
Числовой ряд называют расходящимся, если 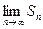 не существует или
не существует или 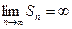 .
.
Пример 1. Рассмотрим ряд 1/2+1/4+1/8+1/16+...+
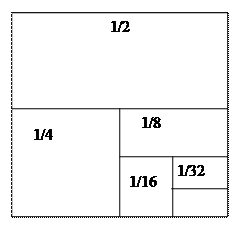 Сторона квадрата равна единице, следовательно площадь 1/2+1/4+1/16+1/32+…. . . = 1
Сторона квадрата равна единице, следовательно площадь 1/2+1/4+1/16+1/32+…. . . = 1
Пример 2. Числовой ряд 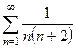 является сходящимся. Это легко доказать, рассмотрев последовательность частичных сумм. Действительно,
является сходящимся. Это легко доказать, рассмотрев последовательность частичных сумм. Действительно,
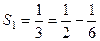 ,
, 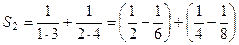 ,
,
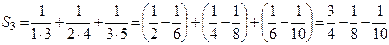 , …,
, …,
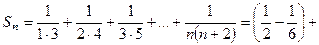
 .
.
Следовательно, 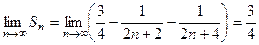 , т.е. ряд сходится.
, т.е. ряд сходится.
Пример 3. Найти сумму ряда 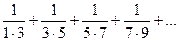 .
.
Решение. Разлагаем общий член ряда на простейшие дроби:
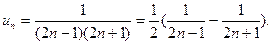 Выписываем несколько членов ряда так, чтобы было видно, какие слагаемые сокращаются при вычислении частичной суммы ряда:
Выписываем несколько членов ряда так, чтобы было видно, какие слагаемые сокращаются при вычислении частичной суммы ряда: 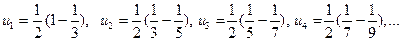 .
.
Составляем 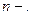 ю частичную сумму ряда:
ю частичную сумму ряда: 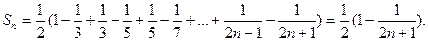 Вычисляем сумму ряда по формуле
Вычисляем сумму ряда по формуле 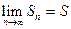 , получаем
, получаем 
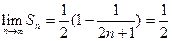 . Ряд сходится и его сумма равна 1/2.
. Ряд сходится и его сумма равна 1/2.
Пример 4. Найти сумму ряда  .
.
Решение. Разложим общий член ряда 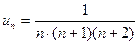 на простейшие дроби с помощью метода неопределенных коэффициентов:
на простейшие дроби с помощью метода неопределенных коэффициентов:
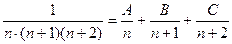 . Умножая на знаменатель левой части, придем к тождеству
. Умножая на знаменатель левой части, придем к тождеству
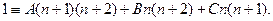
Полагая последовательно 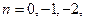 находим: при
находим: при 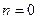 : 1=2A; A=1/2; при
: 1=2A; A=1/2; при 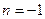 :
: 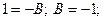 при
при 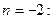
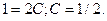 Таким образом,
Таким образом, 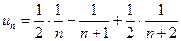 , т.е.
, т.е. 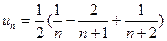 . Выписываем несколько членов ряда, чтобы было видно, какие слагаемые сокращаются при вычислении частичной суммы ряда:
. Выписываем несколько членов ряда, чтобы было видно, какие слагаемые сокращаются при вычислении частичной суммы ряда:
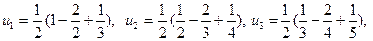
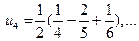
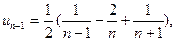
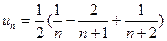 .
.
Составляем  ю частичную сумму ряда и сокращаем все слагаемые, какие возможно:
ю частичную сумму ряда и сокращаем все слагаемые, какие возможно:
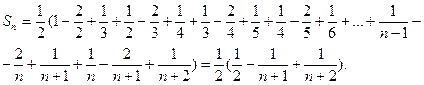
Вычисляем сумму ряда по формуле 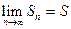 , получаем
, получаем 
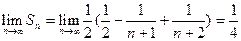 .
.
Числовой ряд 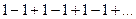 расходится, так как последовательность частичных сумм
расходится, так как последовательность частичных сумм 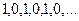
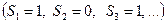 не имеет предела.
не имеет предела.
Известным числовым рядом является геометрическая прогрессия:
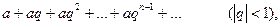
Сумма первых 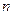 членов прогрессии находится по формуле
членов прогрессии находится по формуле 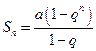 ,
, 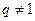 . Предел этой суммы равен:
. Предел этой суммы равен:
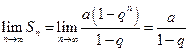 ,
,
если 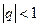 , так как
, так как 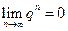 . Если
. Если 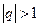 , то
, то 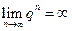 , поэтому
, поэтому 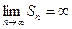 , ряд расходится. Если
, ряд расходится. Если 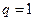 , то ряд принимает вид
, то ряд принимает вид 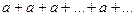 . Последовательность частичных сумм
. Последовательность частичных сумм 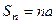 расходится,
расходится, 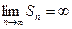 , следовательно, расходится и ряд. При
, следовательно, расходится и ряд. При 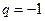 ряд принимает вид
ряд принимает вид 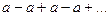 - в этом случае
- в этом случае 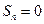 при четном
при четном 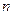 и
и 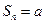 при нечетном
при нечетном 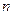 . Следовательно,
. Следовательно, 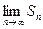 не существует, а ряд расходится.
не существует, а ряд расходится.
Пример 5. Исследовать сходимость ряда 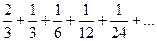 .
.
Решение. Ряд составлен из членов бесконечно убывающей геометрической прогрессии и поэтому сходится. Найдем сумму ряда. Здесь 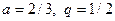 (знаменатель прогрессии) Следовательно,
(знаменатель прогрессии) Следовательно, 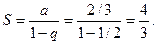
Свойства сходящихся рядов
Теорема 1. Если все члены сходящегося ряда 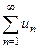 умножить на число
умножить на число 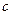 , то ряд
, то ряд 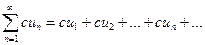 так же сходится и его сумма равна
так же сходится и его сумма равна 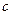
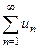 . Если же ряд
. Если же ряд 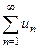 расходится и
расходится и 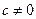 , то и ряд
, то и ряд 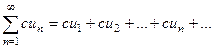 расходится.
расходится.
Доказательство. Обозначим 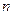 -ю частичную сумму ряда
-ю частичную сумму ряда 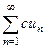 через
через 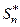 . Тогда
. Тогда
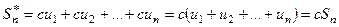 .
.
Следовательно, 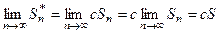 , т.е. ряд
, т.е. ряд 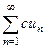 сходится и имеет сумму
сходится и имеет сумму 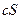 .
.
Покажем теперь, что если ряд 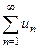 расходится, а число
расходится, а число 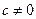 , то и ряд
, то и ряд 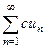 расходится. Допустим противоположное, что ряд
расходится. Допустим противоположное, что ряд 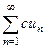 сходится и имеет сумму
сходится и имеет сумму 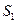 . Тогда
. Тогда  .
.
Отсюда получаем: 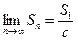 , т.е. ряд
, т.е. ряд 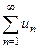 сходится, что противоречит условию.
сходится, что противоречит условию.
Теорема 2.Если сходится ряд 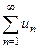 и сходится ряд
и сходится ряд  , а их суммы равны
, а их суммы равны 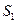 и
и 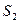 соответственно, то сходятся и ряды
соответственно, то сходятся и ряды 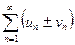 , (), причем сумма каждого равна соответственно
, (), причем сумма каждого равна соответственно 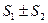 .
.
Доказательство. Обозначим 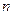 -е частные суммы рядов
-е частные суммы рядов 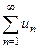 ,
,  , и
, и 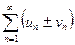 , через
, через 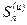 ,
, 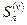 и
и  соответственно. Тогда
соответственно. Тогда
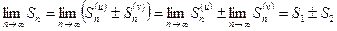 ,
,
т.е. каждый из рядов 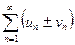 сходится, и сумма его равна
сходится, и сумма его равна 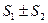 соответственно.
соответственно.
Теорема 3. Если сходится ряд 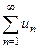 , то сходится и любой ряд, полученный из данного перегруппировкой его членов.
, то сходится и любой ряд, полученный из данного перегруппировкой его членов.
Теорема 4. Если сходится ряд, полученный из исходного ряда 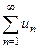 отбрасыванием конечного числа членов, то сходится и исходный ряд, а если сходится числовой ряд
отбрасыванием конечного числа членов, то сходится и исходный ряд, а если сходится числовой ряд 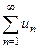 , то сходятся и ряд, полученный отбрасыванием конечного числа членов.
, то сходятся и ряд, полученный отбрасыванием конечного числа членов.
Доказательство. Сумму первых 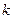 отброшенных членов обозначим
отброшенных членов обозначим 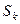 . Оставшиеся члены ряда
. Оставшиеся члены ряда 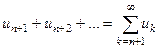 называются
называются 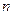 -м остатком ряда. Рассмотрим последовательность частичных сумм оставшихся членов
-м остатком ряда. Рассмотрим последовательность частичных сумм оставшихся членов 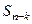 :
: 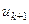 ,
, 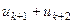 ,
, 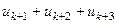 , …. Данная последовательность по условию теоремы является сходящейся, т.е.
, …. Данная последовательность по условию теоремы является сходящейся, т.е.  является некоторым числом
является некоторым числом 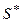 . Рассмотрим последовательность частичных сумм исходного ряда
. Рассмотрим последовательность частичных сумм исходного ряда 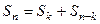 , которая является сходящейся, т.к.
, которая является сходящейся, т.к. 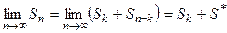 . Это и означает, что исходный числовой ряд тоже сходится. Вторая часть теоремы доказывается с помощью аналогичных рассуждений.
. Это и означает, что исходный числовой ряд тоже сходится. Вторая часть теоремы доказывается с помощью аналогичных рассуждений.
Пример 6.Исследовать сходимость ряда 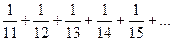 .
.
Решение. Данный ряд получен из гармонического
отбрасыванием первых десяти членов. Следовательно, он
расходится.
Ряд, полученный из данного отбрасыванием конечного числа членов называют 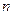 -м остатком исходного ряда и обозначают
-м остатком исходного ряда и обозначают 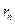 .
.
Теорема 5. Для того, чтобы ряд 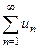 был сходящимся, необходимо и достаточно, чтобы
был сходящимся, необходимо и достаточно, чтобы 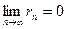 .
.
Доказательство. Так как 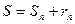 , где
, где 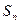 - частичная сумма ряда, то переходя к пределу, получаем:
- частичная сумма ряда, то переходя к пределу, получаем:
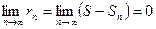
Необходимый признак сходимости числового ряда.
Нахождение 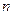 - й частичной суммы
- й частичной суммы 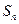 и ее предела не удобно для практического использования. Поэтому для выяснения сходимости ряда устанавливают необходимые и достаточные признаки сходимости. Рассмотрим необходимый признак сходимости.
и ее предела не удобно для практического использования. Поэтому для выяснения сходимости ряда устанавливают необходимые и достаточные признаки сходимости. Рассмотрим необходимый признак сходимости.
Теорема( необходимый признак сходимости) . Если числовой ряд 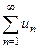 сходится, то его общий член
сходится, то его общий член  стремится к нулю, т.е.
стремится к нулю, т.е. 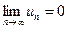 .
.
Доказательство. Пусть числовой ряд 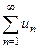 сходится и
сходится и 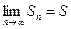 . Тогда и
. Тогда и 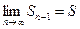 (при
(при 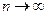 и (
и ( 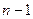 )
) 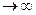 ). Поскольку
). Поскольку 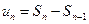 при
при 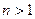 , получаем:
, получаем: 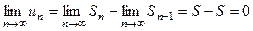 .
.
Следствие. Если  , т.е. необходимое условие сходимости числового ряда не выполняется, то ряд расходится.
, т.е. необходимое условие сходимости числового ряда не выполняется, то ряд расходится.
Пример 7. Исследовать сходимость ряда  .
.
Решение: Ряд  расходится, т.к.
расходится, т.к.
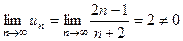 ,
,
т.е. выполняется достаточное условие расходимости ряда.
Пример 8. Исследовать сходимость ряда
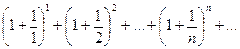
Решение: Данный ряд расходится, т.к. 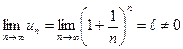 .
.
Необходимый признак сходимости числового ряда не является достаточным: из условия 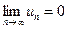 не следует что, ряд сходится. Существует множество расходящихся числовых рядов, для которых
не следует что, ряд сходится. Существует множество расходящихся числовых рядов, для которых 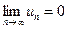 . Например, рассмотрим гармонический ряд
. Например, рассмотрим гармонический ряд
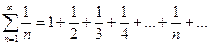 .
.
Очевидно, что 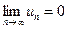 . Однако гармонический ряд расходится. Докажем расходимость гармонического ряда:
. Однако гармонический ряд расходится. Докажем расходимость гармонического ряда:
(1) 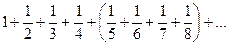
(2) 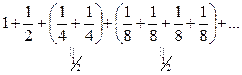
Очевидно сумма ряда (2) больше , чем ряда (1). Ряд (2) расходится, так как 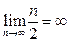 , значит, и гармонический ряд является расходящимся.
, значит, и гармонический ряд является расходящимся.
1.22. Достаточные признаки сходимости числовых рядов.
Сходимость и расходимость числовых рядов с положительными членами можно установить с помощью сравнения его с другим («эталонным») рядом, о котором заранее известно, сходится он или расходится. Такое сравнение производится на основе двух теорем сравнения.
Теорема 1. Пусть даны два знакоположительных ряда 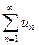 и
и  . Если для всех
. Если для всех 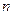 выполняется неравенство
выполняется неравенство 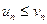 , то из сходимости ряда
, то из сходимости ряда  следует сходимость ряда
следует сходимость ряда 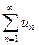 , из расходимости ряда
, из расходимости ряда 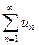 следует расходимость ряда
следует расходимость ряда  .
.
Доказательство. Обозначим 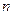 -e частичные суммы рядов
-e частичные суммы рядов 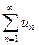 и
и  соответственно через
соответственно через 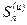 и
и 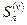 . Суммируя неравенства
. Суммируя неравенства 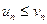 получаем, что
получаем, что 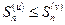 .
.
Пусть ряд  сходится и
сходится и 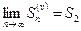 . Члены ряда
. Члены ряда  положительны, поэтому
положительны, поэтому 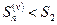 . Используя неравенство
. Используя неравенство 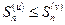 , получаем
, получаем 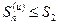 . Последовательность
. Последовательность 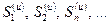 монотонно возрастает, поскольку
монотонно возрастает, поскольку 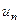 >0, и ограничена сверху числом
>0, и ограничена сверху числом 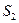 , следовательно, имеет предел
, следовательно, имеет предел 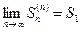 , т. е. ряд
, т. е. ряд 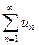 сходится.
сходится.
Пусть теперь знакоположительный числовой ряд 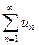 расходится:
расходится: 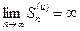 . Тогда, с учетом неравенства
. Тогда, с учетом неравенства 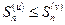 получаем
получаем 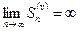 , т. е. ряд
, т. е. ряд  расходится.
расходится.
Теорема 1 имеет место и в том случае, когда неравенство 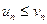 выполняется не для всех членов рядов
выполняется не для всех членов рядов 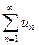 и
и  , а начиная с некоторого номера.
, а начиная с некоторого номера.
Пример 9. Исследовать на сходимость ряд 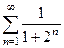 .
.
Решение: Сравним данный ряд с рядом геометрической прогрессии 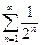 , о котором заранее известно, что он сходится, так как является бесконечно убывающей геометрической прогрессией. Поскольку для любого
, о котором заранее известно, что он сходится, так как является бесконечно убывающей геометрической прогрессией. Поскольку для любого 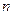 выполняется неравенство
выполняется неравенство 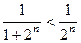 , то из сходимости геометрической прогрессии следует и сходимость ряда
, то из сходимости геометрической прогрессии следует и сходимость ряда 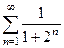 . Следовательно, данный ряд сходится.
. Следовательно, данный ряд сходится.
Пример 10. Исследовать сходимость ряда 
Решение. Так как 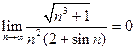 , то необходимое условие сходимости ряда выполнено. Применим первый признак сравнения. Поскольку
, то необходимое условие сходимости ряда выполнено. Применим первый признак сравнения. Поскольку 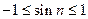 , имеем
, имеем  и, следовательно,
и, следовательно, 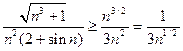 . Так как ряд
. Так как ряд 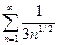 расходится как обобщенный гармонический ряд с
расходится как обобщенный гармонический ряд с 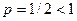 , то по первому признаку сравнения расходится и исходный ряд.
, то по первому признаку сравнения расходится и исходный ряд.
Теорема 2. Пусть даны два знакоположительных ряда 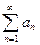 и
и  . Если существует конечный, предел
. Если существует конечный, предел  , то ряды
, то ряды 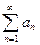 и
и  сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Доказательство. Пусть существует конечный предел, тогда
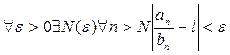 или
или
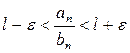 ,
, 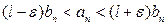 .
.
Если ряд 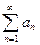 сходится, то из левого неравенства и первой теоремы сравнения следует, что и ряд
сходится, то из левого неравенства и первой теоремы сравнения следует, что и ряд  тоже сходится. Если ряд
тоже сходится. Если ряд 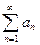 расходится, то из правого неравенства и первой теоремы сравнения вытекает, что и ряд
расходится, то из правого неравенства и первой теоремы сравнения вытекает, что и ряд  тоже расходится. Аналогично, если известна сходимость или расходимость ряда
тоже расходится. Аналогично, если известна сходимость или расходимость ряда  можно сделать вывод о поведении
можно сделать вывод о поведении
ряда 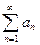
Пример 11. Исследовать сходимость ряда 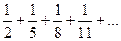 .
.
Решение. Здесь 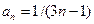 . Сравним ряд с гармоническим рядом, у которого
. Сравним ряд с гармоническим рядом, у которого 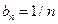 :
: 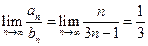 . Следовательно, данный ряд расходится по второму признаку сравнения.
. Следовательно, данный ряд расходится по второму признаку сравнения.
Пример 12. Исследовать сходимость ряда 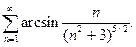
Решение. Так как 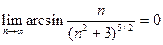 , то необходимое условие сходимости ряда выполнено. Проверяем, что члены данного ряда положительны. Действительно,
, то необходимое условие сходимости ряда выполнено. Проверяем, что члены данного ряда положительны. Действительно, 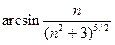 >0 при всех
>0 при всех 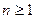 , так как
, так как 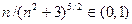 . Имеем
. Имеем 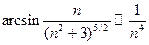 при
при 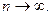 Ряд
Ряд 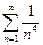 сходится как обобщенный гармонический ряд с
сходится как обобщенный гармонический ряд с 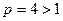 . Следовательно, в силу второго признака сравнения исходный ряд также сходится.
. Следовательно, в силу второго признака сравнения исходный ряд также сходится.
Пример 14. Исследовать сходимость ряда 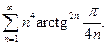
Решение. Поскольку 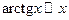 при
при 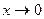 , упрощаем выражение для
, упрощаем выражение для  :
: 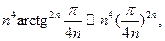 т. е. будем исследовать сходимость ряда
т. е. будем исследовать сходимость ряда 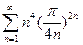 и затем воспользуемся вторым признаком сравнения. Поскольку
и затем воспользуемся вторым признаком сравнения. Поскольку 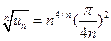 , вычисляем
, вычисляем 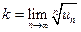 , учитывая, что
, учитывая, что 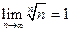 :
: 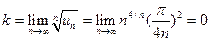 . Так как
. Так как 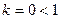 , то ряд
, то ряд 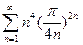 сходится. Следовательно, по второму признаку сравнения сходится и исходный ряд.
сходится. Следовательно, по второму признаку сравнения сходится и исходный ряд.
Пример 15. Исследовать сходимость ряда 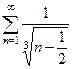 .
.
Решение: Здесь 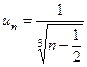 . В качестве эталонного ряда сравнения возьмем расходящийся гармонический ряд с общим членом
. В качестве эталонного ряда сравнения возьмем расходящийся гармонический ряд с общим членом 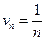 . Имеем
. Имеем 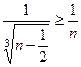 . Следовательно, исходный ряд расходится.
. Следовательно, исходный ряд расходится.
| <== предыдущая лекция | | | следующая лекция ==> |
| А и m законы квантования | | | ОРГАНЫ ДЫХАНИЯ |
Дата добавления: 2015-10-13; просмотров: 3045;
