Краткие обобщенные характеристики прямоугольных изометрической и димитрической проекций

1) Прямоугольная изометрическая проекция. Положение осей приведено Рис. 2.1.

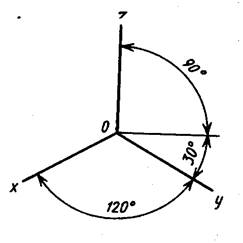
Рис. 2.1

Коэффициент искажения по осям x, y, z равен 0,82. Для упрощения изометрическую проекцию, как правило выполняют без искажения, т.е. приняв коэффициент искажения равным 1.

Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются на аксонометрическую плоскость проекций в эллипсы (см. Рис. 2.2 а).

Рис. 2.2.

В зависимости от принятых коэффициентов искажения длины осей эллипсов 1, 2 и 3 (см. Рис. 2.2 а) при диаметре окружности D будут равны:

- большая ось эллипса рана D, если К_иск=0,82 и 1,22·D, если К_иск=1;

- малая ось эллипса рана 0,58·D, если К_иск=0,82 и 0,71·D, если К_иск=1.

Один из способов построения овала, близкого к эллипсу, в изотермической проекции окружности приведен на Рис. 2.2 б.

Изображение детали в прямоугольной изометрии представлено на Рис. 2.3.

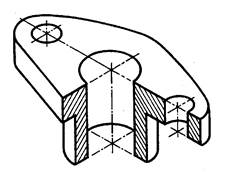
Рис. 2.3.

2) Прямоугольная диметрическая проекция. Положение аксонометрических осей приведено Рис. 2.4.

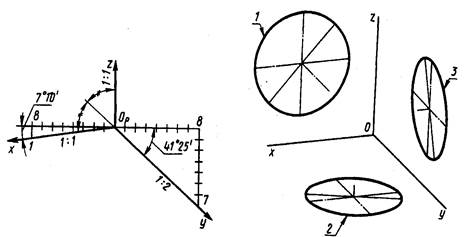
Рис. 2.4. Рис. 2.5.

Коэффициент искажения по оси у равен 0,47, по осям x и z равен 0,94. Для упрощения изображения диметрической проекции, как правило, принимают коэффициент искажения по осям x и z равным 1, а по оси у равным 0,5.

Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются на аксонометрическую плоскость проекций в эллипсы (см. Рис. 2.5).

В зависимости от принятых коэффициентов искажения длины осей эллипсов 1, 2 и 3 (см. Рис. 2.5) при диаметре окружности D будут равны:

- большая ось эллипсов рана D (если К_иск=0,47 и 0,94) и 1,06·D (если К_иск=0,5 и 1);

- малая ось эллипса 1 рана 0,9·D, (если К_иск=0,47 и 0,94) ·0,95·D, (если К_иск=0,5 и 1);

- малая ось эллипсов 2,3 рана 0,33·D, (если К_иск=0,47 и 0,94) ·0,35·D, (если К_иск=0,5 и 1);

Изображение детали в прямоугольной изометрии представлено на Рис. 2.6.

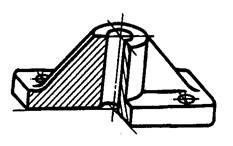
Рис. 2.6

Линии штриховки в аксонометрических проекциях представлены на Рис. 2.7.

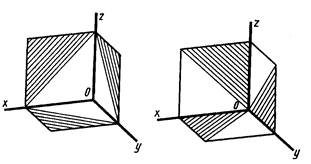
Рис. 2.7