ЦЕНТРАЛЬНОЕ И ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕ

Центральное проецирование — получение проекций с помощью проецирующих лучей, проходящих через точку S, которую называют центром проецирования (рис. 4.3). Если считать лампу точечным источником освещения, то проецирующие лучи выходят из одной точки, следовательно, на плоскости Р получена центральная проекция карандаша (рис. 4.1).

Примером центрального проецирования является проецирование кадров кинофильма или слайдов на экран, где кадр — объект проецирования, изображение на экране — проекция кадра, а фокус объектива — центр проецирования.

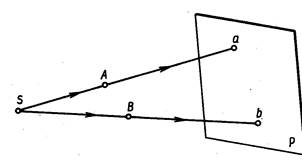
Рис. 4.3

Изображения, получаемые способом центрального проецирования, подобны изображениям на сетчатке нашего глаза. Они наглядны, понятны для нас, так как показывают нам предметы окружающей действительности такими, какими мы их привыкли видеть. Но искажение размеров предметов и сложность построения изображений при центральном проецировании не позволяют использовать его для изготовления чертежей.

Центральные проекции широко применяют лишь там, где нужна наглядность в изображениях, например, в архитектурно-строительных чертежах при изображении перспектив зданий, улиц, площадей и т. п.

Параллельное проецирование. Если центр проецирования — точку S удалить в бесконечность, то проецирующие лучи станут параллельными друг другу. На рис. 4.4 показано получение параллельных проекций точек А и В на плоскости Р.

В зависимости от направления проецирующих лучей по отношению к плоскости проекций параллельные проекции делятся на косоугольные и прямоугольные.

При косоугольном проецировании угол наклона проецирующих лучей к плоскости проекций не равен 90^о (рис. 4.5).

При прямоугольном проецировании проецирующие лучи перпендикулярны плоскости проекций (рис. 4.6).

Рассмотренные выше способы проецирования не устанавливают взаимно однозначного соответствия между объектом (точка А) и его изображением (проекцией). При заданном направлении проецирующих лучей на плоскости проекций всегда получается лишь одна проекция точки, но судить о положении точки в пространстве по одной ее проекции невозможно, так как на одном и том же проецирующем луче Аа (рис. 4.7) точка может занимать различные положения, находясь выше или ниже заданной точки А, и какое положение точки в пространстве соответствует изображению (проекции) а, определить невозможно.

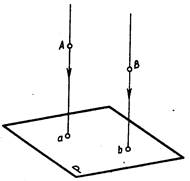
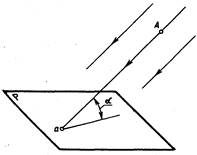
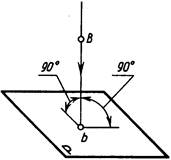
Рис. 4.4. Рис. 4.5. Рис. 4.6.

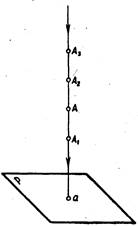
Рис. 4.7.

Для того чтобы по изображению точки можно было определить ее положение в пространстве, необходимо как минимум иметь две проекции этой точки. При этом должно быть известно взаимное расположение плоскостей проекций и направление проецирования. Тогда, имея два изображения точки А, можно будет представить, как расположена точка в пространстве.

Наиболее простым и удобным является проецирование на взаимно перпендикулярные плоскости проекций с помощью проецирующих лучей, перпендикулярных плоскостям про­екций.

Такое проецирование называют ортогональным проецированием, а полученные изображения — ортогональными проекциями.