ЗАТУХАЮЩИЕ КОЛЕБАНИЯ

В реальных условиях всегда происходит затухание механических колебаний, т.е. постепенное ослабление колебаний со временем, обусловленное потерей энергии колебательной системой вследствие трения и других причин.

Рассмотрим случай, когда колеблющееся тело находится в вязкой среде, а его скорость v небольшая. Тогда на тело действует сила сопротивления, равная

,

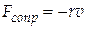(8)

где r — коэффициент сопротивления, который зависит от формы тела и вязкости среды.

Результирующая сила, которая действует на тело, равняется сумме квазиупругой силы и силы сопротивления:

.

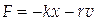Составим уравнение движения, используя второй закон Ньютона:

.

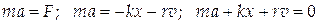(9)

Принимая во внимание, что 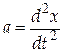, , 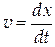и поделив уравнение (9) на массу m, получим:

.

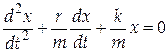Введем обозначение:

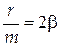(b– коэффициент затухания); 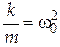(см. формулу (7));

w_o – циклическая частота незатухающих колебаний.

Тогда

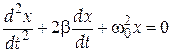- (10)

- дифференциальное уравнение затухающих колебаний.

Если пренебречь силами сопротивления (т.е. положить 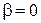), то уравнение (10) переходит в уравнение гармонических колебаний (4), которое имеет решение:

,

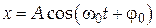где амплитуда А = const.

Если же b¹0, но не слишком большое (т.е. b <w_o), то уравнение (10) имеет решение

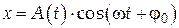, (11)

где

–

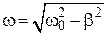(12)

циклическая частота затухающих колебаний;

–

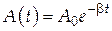(13)

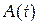– амплитуда затухающих колебаний (А₀ – начальная амплитуда).

Зависимости x(t) и A(t) для затухающих колебаний показаны на рис. 2.

Введем некоторые характеристики затухающих колебаний.

Период Т затухающих колебаний равняется

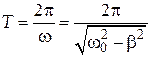. (14)

Логарифмический декремент затухания численно равен натуральному логарифму отношения амплитуд затухающих колебаний, взятых через промежуток времени, равному периоду колебаний:

.

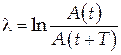(15)

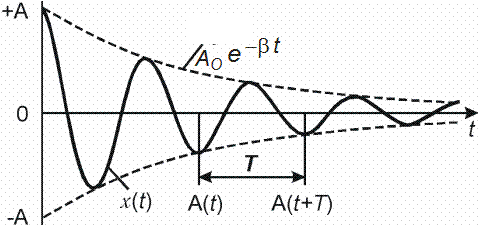
Рис. 2

Подставим (13) в (15):

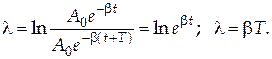(16)

Получили связь между логарифмическим декрементом затухания 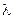и коэффициентом затухания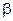

Логарифмический декремент затухания характеризует скорость затухания: чем больше 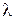, тем быстрее затухают колебание.

Добротность колебательной системы пропорциональна отношению энергии системы в момент времени t к потерям энергии за время, равное периоду колебаний:

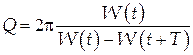. (17)

Чем больше добротность системы, тем медленнее убывает ее энергия и, следовательно, тем дольше сохраняются колебания в системе.

Добротность системы и логарифмический декремент затухания связаны соотношениям

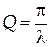. (18)

Трифилярный подвес, секундомер, миллиметровая бумага, песок.

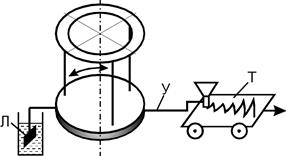Рис. 3.

В данной работе затухающие колебания изучаются на диске, подвешенному на трифилярном подвесе (рис. 3). При отклонении диска на некоторый угол в горизонтальной плоскости он начинает выполнять колебания. К диску укреплен указатель У, к концу которого присоединена воронка с песком. При движении тележки Т песок вычерчивает на бумаге, помещенной на тележке, затухающие колебания. Затухания обеспечивается лопаточкой Л, которая движется в сосуде с вязкой жидкостью.

1. Размещают на тележке лист миллиметровой бумаги так, чтобы при протягивании тележки указатель все время находился над одной и той же линией миллиметровой бумаги. На этой линии на расстоянии ~15 см отмечают две точки и проводят через них прямую. Снова устанавливают тележку в такое положение, чтобы указатель находился немного впереди (~2 см) начальной метки. Включают протягивание тележки. В момент совпадения начальной метки с указателем включают секундомер, а при совпадении с последней меткой – выключают. Тем самым измеряют время t, за которое тележка сместится на заданное расстояние L. По этим данным можно рассчитать цену деления миллиметровой бумаги, решая пропорцию

L мм – t, с

1 мм – t_о, с.

Отсюда t_о=t/L, с/мм.

2. Снова устанавливают тележку в такое положение, чтобы указатель находился немного впереди (~2 см) начальной метки. Отклоняют указатель (воронку с предварительно насыпанным песком) на угол 10^о. Потом одновременно включают тележку и отпускают указатель. Песок, который высыпается из воронки, вычерчивает на бумаге затухающие колебания.

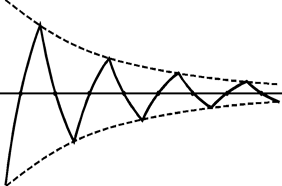Рис. 4

3. Отмечают на кривой затухающих колебаний точки пересечения с центральной линией, а также максимальные и минимальные значения и потом вытряхивают песок. По имеющимся точкам воссоздают график затухающих колебаний (рис. 4). Начальная метка служит началом отсчета времени. Снизу и сверху профиля затухающих колебаний проводят огибающую, которая представляет собой зависимость амплитуды затухающих колебаний от времени.