МЕХАНИЧЕСКИЕ ГАРМОНИЧНЫЕ КОЛЕБАНИЯ.

Периодические колебания величины x(t) называется гармоничными, если она изменяется по закону синуса или косинуса.

В дальнейшем мы будем рассматривать гармонические колебания, которые изменяются по закону косинуса

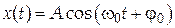
(1)

Здесь w_o – циклическая частота гармонических колебаний; 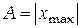– амплитуда колебаний, т.е. максимальное по модулю значение колебательной величины x; 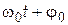– фаза; 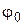– начальная фаза колебаний.

Зная фазу колебаний, можно определить величину смещения xв данный момент времени. Начальная фаза колебаний показывает величину смещения от положения равновесия в начальный момент времени, т.е. при t=0:

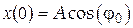
Дифференцируя уравнение (1) по времени, получим выражение для скорости

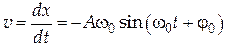
(2)

Выражение для ускорения получим, продифференцировав(2) по времени

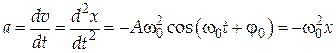
(3)

или

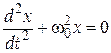(4)

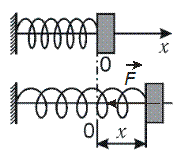Рис. 1.

Уравнение (4) представляет собой дифференциальное уравнение гармоничных колебаний.

Пример: колебания пружинного маятника. Пружинный маятник представляет собой тело массой m, прикрепленное к абсолютно упругой пружине (рис. 1). При смещении тела на величину x от положения равновесия соответственно закону Гука возникает сила упругой деформации:

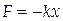(5)

Если после смещения тела от положения равновесия отпустить его, то маятник начнет выполнять колебания. Составим уравнение движения пружинного маятника. По второму закону Ньютона

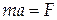
Поскольку 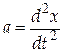, то с учетом (5) получим

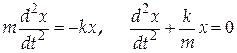
(6)

Сравнивая (6) и (4), мы видим, что пружинный маятник выполняет гармоничные колебания. При этом циклическая частота колебаний пружинного маятника

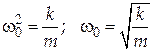
(7)

Много сил, которые не являются упругими по своей природе, также могут удовлетворять соотношению (5). Такие силы объединены общим названием квазиупругих. Квазиупругая сила пропорциональна смещению от положения равновесия и всегда направлена к положению равновесия. При этом параметр k в (5) называют квазиупругой постоянной.