Модель Максвелла
При послідовному з’єднанні маємо модель, яка називається моделлю Максвела (рис.3.7).
Рис 3.7. Модель Максвелла
При такому з’єднанні пружного і в'язкого елементів загальна деформація цих двох елементів дорівнює сумі деформацій кожного елемента, а напруження (зусилля) в елементах однакові.
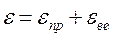, (3)
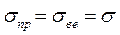. (4)
Диференціюємо (1):
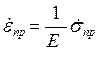. (5)
Зміна напружень зі швидкістю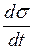 
викликають зміну (миттєву реакцію) 
.
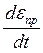Диференціюємо (3) після підстановки (2) і (5) з урахуванням (4), одержуємо загальне диференційне рівняння деформування в'язко-пружного тіла за моделлю Максвелла:
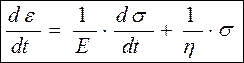. (6)
––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––
Примітка. Застосуванні механічних моделей при описанні в’язко-пружних процесів приводить до лінійних диференціальних рівнянь типу
. (*)
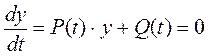Його загальне рішення має вигляд:
. (**)
––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––
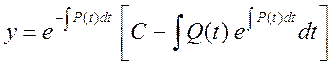При ε = ε0 = const (релаксація напружень, рис. 3.2а) з (6) одержуємо:
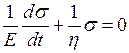
або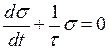 
, (7)
де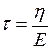 
.
Зіставляючи (7) з (*) отримуємо загальний розв'язок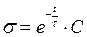 
.
З урахуванням початкових умов (при t = 0: σ = σ 0)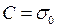 
.
Остаточно одержуємо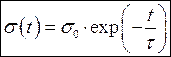 
. (8)
де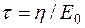 
- час релаксації, тобто час, за який напруження зменшуються в е раз (при 
, 
, 
).
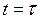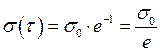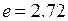Пр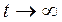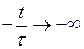и 
и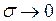 
, тобто при великому часі 
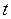значення напруження 
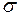знижується до нуля.
Коефіцієнт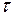 
характеризує швидкість процесу релаксації, тобто чим більше 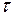, тим менше швидкість релаксації. Більшому потенційному бар'єру обертання макромолекул, відповідає більший час релаксації 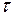. З підвищенням температури полімеру 
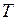, час релаксації 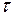зменшується (збільшується рухомість сегментів макромолекул).
Рівняння (8) якісно описує криву релаксацію напружень лінійних аморфних полімерів (рис. 3.2б).
Спосіб визначення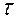 
за експериментальними даними.
Логарифмуємо (8) і одержуємо: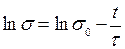 
.
При будь-якому t = t′ напруження σ = σ′ (рис. 3.8)
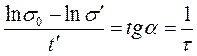. Таким чином, 
.
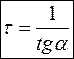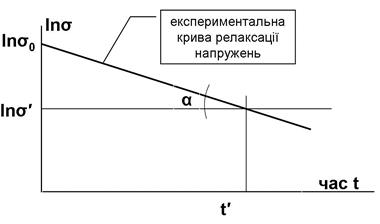
Рис. 3.8. Схема, що пояснює спосіб визначення часу релаксації
Рівняння (8) можна записати за аналогією із законом Гука в операторному вигляді:
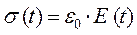, (9)
де 
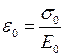, а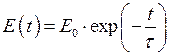 
,
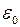- миттєва деформація,
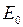- миттєвий модуль пружності,
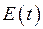- модуль релаксації (або функція релаксації).
Зауваження.Рівняння (8) не відображає процес повзучості при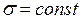 
.
У цьому випадку з (8) маємо: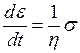 
. Зіставивши це рівняння з (*) та (**), отримаємо: 
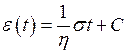. При початкових умовах ( 
) 
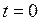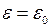та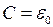 
.
У кінцевому вигляді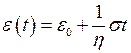 
(рис.3.9).
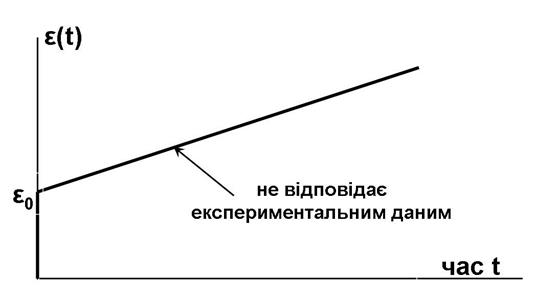
Рис. 3.9. Крива повзучості за моделлю Максвела
Дата добавления: 2015-10-09; просмотров: 792;