Правило наименьших издержек и правило максимизации прибыли

Правило наименьших издержек – это условие, согласно которому издержки минимизируются в том случае, когда последний рубль, затраченный на каждый ресурс, дает одинаковую отдачу (одинаковый предельный продукт):

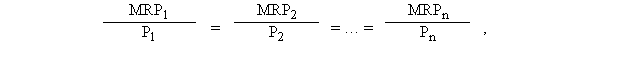
где MRP_i - предельный продукт i-того фактора в денежном выражении;

Р_i - цена i-того фактора.

Это правило обеспечивает равновесие положения производителя. Когда отдача всех факторов одинакова, задача их перераспределения отпадает, т.к. уже нет ресурсов, которые приносят больший доход по сравнению с другими.

Предельная производительность ресурса является мерой его вклада в производство благ. Этот вклад зависит не только от его свойств, но и от тех пропорций, которые существуют между ним и другими ресурсами.

В какой степени нужен тот или иной ресурс в производстве? Чем определяется степень его использования? Прежде всего, разницей между доходом, который он приносит, и издержками, связанными с его использованием. Рациональный производитель стремится максимизировать эту разность.

При совершенной конкуренции цены благ и цены ресурсов являются заданными. Отсюда можно сделать вывод, что предельная производительность какого-либо ресурса в денежном выражении будет иметь ту же динамику изменения, что и предельная производительность в натуральном выражении, т.к., чтобы получить первую, нужно вторую умножить на постоянную цену. Ресурс поэтому будет находить применение в производстве до тех пор, пока его предельная производительность в денежном выражении будет не ниже его цены:

MRP₁ ≥ Р₁.

Правило максимизации прибыли на конкурентных рынках означает, что предельные продукты всех факторов производства в стоимостном выражении равны их ценам, или что каждый ресурс используется до тех пор, пока его предельный продукт в денежном выражении не станет равен его цене:

MRP_i = Р_i.