ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ

1)Точечные оценки оценивают неизвестное значение параметра одним числом. Недостатком точечных оценок является то, что в них не указывается точность оценки параметра при выборках конечного объёма. Можно лишь сказать, что при n→∞ оценки параметров сходятся по вероятности к истинным значениям этих параметров. Иногда удобнее оценивать значение параметра с помощью интервала, в который это значение попадает с определённой вероятностью.

Пусть θ – оцениваемый параметр, а θ₁ и θ₂ – две функции элементов выборки x₁, x_2, …, x_n, такие, что θ₁ < θ₂. Если выполняется соотношение

P{θ₁ < θ < θ₂} = γ, (1)

то интервал (θ₁, θ₂) называется 100 γ-процентным доверительным интервалом параметра θ. Другими словами, доверительный интервал – это интервал, в котором с заданной вероятностью находится значение неизвестного параметра. Значения θ₁ и θ₂ называют соответственно нижней и верхней границами доверительного интервала, а γ – доверительной вероятностью или коэффициентом доверия. Неважно, каким образом были получены границы интервала θ₁ и θ₂, важен сам факт выполнения соотношения (1). Доверительный интервал даёт определённую информацию о точности оценки данного параметра.

Для построения доверительного интервала необходимо знать тот или иной закон распределения вероятностей. Предположим, например, что неизвестный параметр θ можно интерпретировать как некоторую случайную величину с известной плотностью распределения вероятностей f(θ). Пусть θ* = θ*(x₁, x₂, …, x_n) – точечная оценка параметра θ. Тогда в некоторых случаях можно определить условную плотность распределения вероятностей

и из соотношения

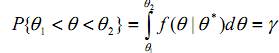
можно определить границы θ₁ и θ₂ доверительного интервала с доверительной вероятностью γ.

Однако не всегда можно задать неизвестный параметр плотностью распределения вероятностей. Обычно неизвестный параметр является некоторой постоянной величиной. Поэтому при построении доверительного интервала пользуются не условной плотностью распределения f(θ | θ*), а условной плотностью f(θ* | θ).

2) Рассмотрим один из возможных способов построения доверительного интервала с использованием этой плотности. Зададим некоторую доверительную вероятность γ и рассмотрим соотношение P{| θ* – θ | < δ} = γ.

Это соотношение определяет симметричный относительно θ доверительный интервал. Рассматривая это соотношение как уравнение относительно δ, можно определить δ, используя известную плотность f(θ*|θ). Тем самым доверительный интервал будет найден. Действительно,

P{| θ* – θ | < δ} = P{–δ < θ* – θ < δ} = P{θ – δ < θ* < θ + δ} = P{θ* – δ < θ < θ*+δ} = γ.

Последнее равенство означает, что θ ∈(θ* – δ, θ* + δ) с вероятностью γ. Данные соотношения показывают, что при построении доверительного интервала можно исходить как из плотности f(θ* | θ), так и из плотности

f(θ | θ*).

Величина δ определяет ширину доверительного интервала. Для фиксированного значения доверительной вероятности γ и для неизменной плотности f(θ* | θ) эта величина является постоянной. Границы доверительного интервала определяются равенствами θ = θ*−δ и θ = θ* + δ. Если считать θ и θ* переменными, то эти два равенства являются уравнениями прямых линий. Вся область, заключённая между этими прямыми, называется доверительной областью (рис. 1). Располагая доверительной областью можно определить доверительный интервал для любого значения оценки θ*. На рисунке указаны границы доверительного интервала θ₁ и θ₂ для произвольного значения оценки θ*.

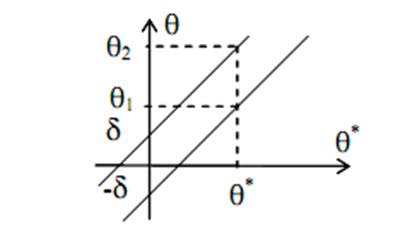
Рис.1.Доверительная область с прямолинейными границами

Границы доверительной области не обязательно являются прямыми линиями. Форма доверительной области определяется структурой самой оценки и, прежде всего, видом закона распределения f(θ* | θ). Здесь рассмотрен самый простой случай построения доверительной области. На рис. 2 изображена доверительная область для неизвестной вероятности события. Границами этой области является линия эллипса.

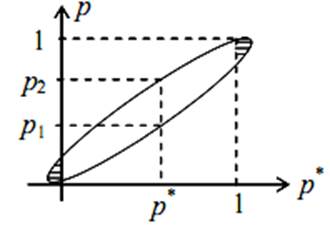
Рис.2. Доверительная область в форме эллипса

Для дискретных случайных величин не всегда можно найти доверительный интервал, имеющий коэффициент доверия, в точности равный γ, если γ задано произвольно. Это связано с тем, что закон распределения дискретной случайной величины имеет ступенчатый характер.

Установление доверительного интервала не означает того факта, что неизвестный параметр принадлежит этому интервалу. Можно лишь утверждать, что с вероятностью γ этот параметр находится внутри интервала. При этом, разумеется, с вероятностью 1 – γ данный параметр находится вне этого интервала. Доверительную вероятность γ выбирают достаточно большой (γ = 0,9 ÷ 0,99). Следует иметь в виду, что при увеличении доверительной вероятности увеличивается длина доверительного интервала. Таким образом, при выборе значения доверительной вероятности следует придерживаться разумного компромисса. Если есть необходимость повысить доверительную вероятность при сохранении длины дове-рительного интервала, то нужно увеличить объём выборки.