Лекция №2: «ТОЧЕЧНЫЕ ОЦЕНКИ ПАРАМЕТРОВ.

СВОЙСТВА ЭМПИРИЧЕСКИХ ХАРАКТЕРИСТИК»

1. Точечные оценки параметров

2. Свойства эмпирических характеристик

3. Методы нахождения оценок параметров

ЛИТЕРАТУРА

1. Морозов Ю.В. Основы высшей математики и статистики. М., «Медицина», 2004, § 9.3.

2. Павлушков И.В. и др. Основы высшей математики и математической статистики. М., «ГЭОТАР-Медиа», 2006, § 8.2.

1) Требуется оценить некоторый параметр θ, связанный со случайной величиной X, используя выборку X_n = {x₁, x₂, …, x_n}. Пусть в качестве такой оценки выбрана однозначная функция от элементов выборки θ* = θ*(x₁, x₂, …, x_n). Для конкретных значений элементов выборки эта оценка представляет собой одно число. Такие оценки называются точечными оценками параметров, так как на числовой оси они изображаются одной точкой. Числовые характеристики случайных величин, найденные на основе экспериментальных данных, называются точечными оценками этих характеристик или эмпирическими характеристиками.

Задача состоит в том, чтобы найти такую оценку θ*, которая была бы в определённом смысле наиболее близкой к оцениваемому параметру θ.

Как функция элементов выборки, оценка θ* является случайной величиной. Определим её математическое ожидание. Оно, очевидно, будет зависеть от истинных числовых характеристик изучаемой величины X и от объёма выборки n. Пусть получено равенство:

M{θ*} = θ + φ(θ, n), (1)

где φ(θ, n) – некоторая функция истинного значения параметра θ. Желательно, чтобы функция φ(θ, n) равнялась нулю. Это бы означало, что математическое ожидание оценки параметра равно истинному значению этого параметра.Оценка θ*, обладающая таким свойством, называется несмещённой оценкой параметра θ. Если φ(θ, n)≠ 0, то θ* называется смещённой оценкой параметра θ, а сама функция φ(θ, n) называется смещением.

Если при n→∞ оценка параметра сходится по вероятности к истинному значению параметра, то оценка θ* называется состоятельной оценкой параметра θ. Для дальнейшего изучения свойств оценки θ* можно определить её дисперсию, которая также окажется функцией от истинных числовых характеристик изучаемой случайной величины X и от объёма выборки n, т.е. D{θ*} = D(θ, n). Если оценка состоятельная, то D(θ, n) стремится к нулю при n→∞. Различные оценки одного и того же параметра будут иметь разные дисперсии. Та из них, которая имеет наименьшую дисперсию, называется эффективной оценкой данного параметра.

2) Проведём краткий анализ эмпирических числовых характеристик. Найдём математическое ожидание и дисперсию оценки m_x* истинного математического ожидания m_x случайной величины X:

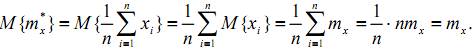
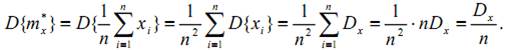
Здесь учтено, что элементы выборки x_i, являясь независимыми реализациями случайной величины X, имеют те же самые характеристики, что и сама величина X. Таким образом,

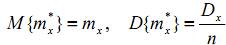, (2)

Из этого следует, что m_x* является несмещённой и состоятельной оценкой истинного математического ожидания m_x случайной величины 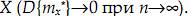Аналогичный анализ для эмпирической дисперсии D_x* показывает, что

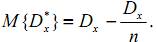
Таким образом, эмпирическая дисперсия является смещённой оценкой дисперсии. Смещение равно (–D_x/n) и стремится к нулю при n→∞. Однако при малом объёме выборки это смещение оказывается существенным. Для его устранения вводится поправочный коэффициент, при умножении которого на D_x* получается другая оценка дисперсии, не имеющая смещения. Эта оценка обозначается обычно через S²:

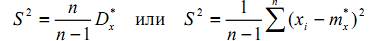, (3)

Очевидно, что M{S²} = D_x.

Вычисление дисперсии величины S² не представляет принципиальных трудностей, но оказывается достаточно громоздким. Вычисления показывают, что эта дисперсия пропорциональна величине 1/n и, следовательно, стремится к нулю при n→∞. Таким образом, величина S² является несмещённой и состоятельной оценкой истинной дисперсии D_x. Её рекомендуется использовать вместо оценки D_x*, особенно при малых значениях n.

3) Рассмотрим кратко методы нахождения оценок. Один из методов предполагает задание структуры оценки с точностью до неизвестных параметров, которые определяются из условия минимума дисперсии оценки. Примером применения этого метода является определение оценки математического ожидания случайной величины в случае неравноточных измерений. Пусть по выборке X_n = {x₁, x₂, …, x_n} требуется оценить параметры m_x и D_x, причём измерения x_i были произведены с разной точностью, т.е.

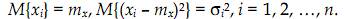
Чем меньше дисперсия измерения, тем больше доверия этому измерению, т.е. измерения должны учитываться оценкой с разными весовыми коэффициентами. Исходя из этого, выберем следующую структуру оценки:

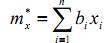, (4)

Чтобы оценка была несмещённой, необходимо выполнение условия:

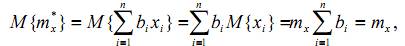
Проводя минимизацию, получим:

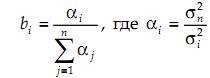, (5)

Итак, при неравноточных измерениях для оценки математического ожидания следует пользоваться формулой (4), подставляя в неё коэффициенты b_i из (5).

Второй метод – метод наибольшего правдоподобия. Этот метод требует знания закона распределения случайной величины с точностью до неизвестных параметров. Предположим, что плотность распределения вероятностей величины X равна f_X(x, θ), где θ – неизвестный параметр, который требуется оценить. Тогда каждое измерение x_i из выборки X_n = {x₁, x₂, …, x_n} будет иметь плотность распределения f_X(x_i, θ). Элементы выборки x_i являются статистически независимыми, поэтому n – мерная плотность распределения вероятностей выборки равна произведению одномерных плотностей, т.е.

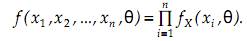(6)

Эту плотность называют функцией правдоподобия. Можно предполагать, что в выборке чаще встречаются те возможные значения величины X, для которых плотность распределения имеет относительно большие значения. Из этого следует, что в качестве оценки параметра θ логично взять такое значение, которое максимизирует функцию правдоподобия. Однако с целью упрощения вычислений используют не функцию правдоподобия непосредственно, а её натуральный логарифм:

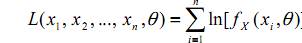, (7)

Доказано, что эта функция имеет максимум, причём значение θ = θ*(x₁, x₂, …, x_n), при котором достигается этот максимум, является оценкой параметра θ, обладающей наименьшей дисперсией. Таким образом, для определения оценки нужно решить уравнение

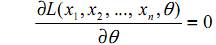, (8)

Решение этого уравнения θ*( x₁, x₂, …, x_n) и будет оценкой параметра θ. Оценки, найденные таким способом, называются оценками максимального (или наибольшего) правдоподобия. Оценки максимального правдоподобия всегда являются эффективными оценками.

Пример 1. По выборке объёма n = 20 найдена оценка дисперсии D_x* случайной величины X: D_x* = 4,8. Определить несмещённую оценку S² неизвестной дисперсии.

Решение. Воспользуемся формулой (3):

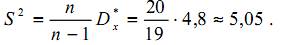
Пример 2. Некоторая постоянная величина C была измерена тремя измерительными приборами по 4 раза каждым. Измерения, полученные с помощью первого прибора, равны 4,75, 4,9, 5,05, 4,85, с помощью второго прибора – 4,9, 5,1, 4,7, 5,15, с помощью третьего прибора – 4,7, 4,95, 5,05, 5,25. Класс точности измерительных приборов такой, что первый из них обеспечивает среднее квадратическое отклонение измерений σ₁ = 0,1, второй – σ₂ = 0,15, третий – σ₃ = 0,2. Требуется оценить истинное значение величины C.

Решение. Измерения величины C являются неравноточными. Поэтому применим для оценки формулу (4). Вычислим коэффициенты b_i по формулам (5):

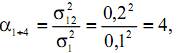
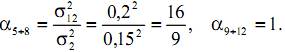
Поскольку каждым прибором было сделано по 4 измерения, то n = 12, и, следовательно,

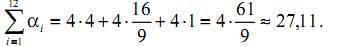
Таким образом,

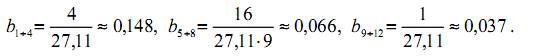
Подставим найденные значения и соответствующие измерения в формулу (5):

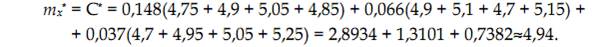
Итак, в качестве оценки истинного значения величины C следует взять C*= 4,94.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Какие оценки параметров распределения называются точечными?

2. Что такое эмпирические характеристики?

3. Какая оценка параметра распределения называется несмещенной? смещенной? состоятельной? эффективной?

4. Что является смещенной и состоятельной оценкой истинного математического ожидания случайной величины?

5. Приведите формулу для смещенной оценки дисперсии.

6. Как определяется оценка математического ожидания при неравноточных измерениях?

7. Что называется функцией правдоподобия?

8. Какие оценки являются оценками наибольшего правдоподобия?