Історія досліджень в області нейронних мереж

Історія досліджень в області нейронних мереж.

Модель нейронної мережі зі зворотним поширенням помилки (back propagation).

Історія досліджень в області нейронних мереж

В історії досліджень в області нейронних мереж, як і в історії будь-якої науки, були свої успіхи і невдачі. Крім того, тут постійно позначається психологічний фактор, що проявляється в нездатності людини описати словами те, як вона думає.

Здатність нейронної мережі до навчання вперше досліджена Дж. Маккалоком і У. Піттом. В 1943 році світ побачила їхня робота "Логічне вирахування ідей, що ставляться до нервової діяльності", у якій була побудована модель нейрона і сформульовані принципи побудови штучних нейронних мереж.

Великий поштовх розвитку нейрокібернетики дав американський нейрофізіолог Френк Розенблатт, який запропонував в 1962 році свою модель нейронної мережі – перцептрон. Сприйнятий спочатку з більшим ентузіазмом, він незабаром піддався інтенсивним нападкам з боку великих наукових авторитетів. І хоча докладний аналіз їхніх аргументів показує, що вони заперечували не зовсім той перцептрон, який пропонував Розенблатт, великі дослідження щодо нейронних мереж були згорнуті майже на 10 років.

Незважаючи на це в 70-і роки було запропоновано багато цікавих розробок, таких, наприклад, як когнітрон, здатний добре розпізнавати досить складні образи незалежно від повороту і зміни масштабу зображення.

В 1982 році американський біофізик Дж. Хопфілд запропонував оригінальну модель нейронної мережі, названу його ім'ям. У наступні кілька років було розроблено безліч ефективних алгоритмів: мережа зустрічного потоку, двонаправлена асоціативна пам'ять і ін.

У Київському інституті кібернетики з 70-х років ведуться роботи над стохастичними нейронними мережами.

2. Модель нейронної мережі зі зворотним поширенням помилки (back propagation)

В 1986 році Дж. Хінтон і його колеги опублікували статтю з описом моделі нейронної мережі і алгоритмом її навчання, що дало новий поштовх дослідженням в області штучних нейронних мереж.

Нейронна мережа складається з безлічі однакових елементів – нейронів, тому почнемо з них розгляд роботи штучної нейронної мережі.

Біологічний нейрон моделюється як пристрій, що має кілька входів (дендрити) і один вихід (аксон). Кожному входу ставиться у відповідність деякий ваговий коефіцієнт (w), який характеризує пропускну здатність каналу і оцінює ступінь впливу сигналу із цього входу на сигнал на виході. Залежно від конкретної реалізації, оброблювані нейроном сигнали можуть бути аналоговими або цифровими (1 і 0). У тілі нейрона відбувається зважене підсумовування вхідних порушень, і далі це значення є аргументом активаційної функції нейрона, один з можливих варіантів якої представлений на рис. 1.

Будучи з'єднаними певним чином нейрони утворюють нейронну мережу. Робота мережі розділяється на навчання й адаптацію. Під навчанням розуміється процес адаптації мережі до пропонованих еталонних зразків шляхом модифікації (згідно з тим або іншим алгоритмом) вагових коефіцієнтів зв'язків між нейронами. Відмітимо, що цей процес є результатом алгоритму функціонування мережі, а не попередньо закладених у неї знань людини, як це часто буває в системах штучного інтелекту.

Серед різних структур нейронних мереж (НМ) однією з найбільш відомих є багатошарова структура, у якій кожен нейрон довільного шару зв'язаний з усіма аксонами нейронів попереднього шару або, у випадку першого шару, з усіма входами НМ. Такі НМ називаються повнозв’язними.

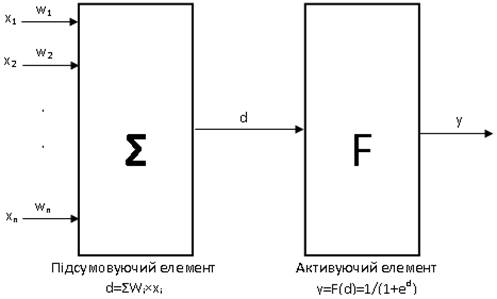
Рис. 1. Штучний нейрон

Коли в мережі є тільки один шар, то алгоритм її навчання із учителем досить очевидний, тому що правильні вихідні стани нейронів єдиного шару свідомо відомі, і підстроювання синаптичних зв'язків ідуть у напрямку, який мінімізує помилку на виході мережі. За таким принципом будується, наприклад, алгоритм навчання одношарового перцептрона. У багатошаровій же мережі оптимальні вихідні значення нейронів всіх шарів, крім останнього, як правило, не відомі, і більш ніж двошаровий перцептрон уже неможливо навчити, керуючись тільки величинами помилок на виходах НМ. Один з варіантів вирішення цієї проблеми – розробка наборів вихідних сигналів, які відповідали б вхідним для кожного шару НМ, що, звичайно, є дуже трудомісткою операцією і не завжди здійсненною. Другий варіант – динамічне підстроювання вагових коефіцієнтів синапсів, у ході якого вибираються, як правило, найбільш слабкі зв'язки і змінюються на малу величину в той чи інший бік, а зберігаються тільки ті зміни, які спричинили зменшення помилки на виході всієї мережі. Очевидно, що даний метод "тику", незважаючи на свою гадану простоту, вимагає громіздких рутинних обчислень. І, нарешті, третій, більше прийнятний варіант – поширення сигналів помилки від виходів НМ до її входів, у напрямку, зворотному прямому поширенню сигналів у звичайному режимі роботи. Цей алгоритм навчання НМ одержав назву процедури зворотного поширення. Саме він буде розглянутий надалі.

Відповідно до методу найменших квадратів, що мінімізується цільовою функцією помилки НМ є величина:

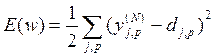, (1)

де 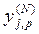– реальний вихідний стан нейрона j-го вихідного шару N-нейронної мережі при подачі на її входи p-го образу; d_j,p – ідеальний (бажаний) вихідний стан цього нейрона.

Підсумовування ведеться по всіх нейронах вихідного шару і по всіх оброблюваних мережею образах. Мінімізація ведеться методом градієнтного спуску, що означає підстроювання вагових коефіцієнтів у такий спосіб:

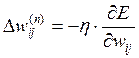. (2)

Тут w_ij – вагові коефіцієнти синаптичного зв'язку, що з'єднує i-ий нейрон шару n–1 з j-им нейроном шару n, η – коефіцієнт швидкості навчання, 0<η<1.

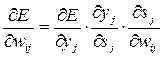. (3)

Тут під y_j, як і раніше, мається на увазі вихід нейрона j, а під s_j – зважена сума його вхідних сигналів, тобто аргумент активаційної функції. Через те, що множник dy_j/ds_j є похідною цієї функції по її аргументу, із цього виникає вимога, щоб похідна активаційної функції була визначена на всій осі абсцис. У зв'язку з цим функція одиничного стрибка та інші активаційні функції з неоднорідностями не підходять для розглянутих НМ. У них застосовуються такі гладкі функції, як гіперболічний тангенс або класичний сигмоїд з експонентою. У випадку гіперболічного тангенса

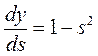. (4)

Третій множник 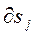/ 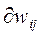дорівнює виходу нейрона попереднього шару y_i^(n-1).

Що стосується першого множника в (3), то він легко розкладається в такий спосіб:

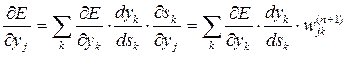. (5)

Тут підсумовування по k виконується серед нейронів шару n+1. Увівши нову змінну

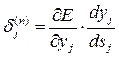(6)

ми одержимо рекурсивну формулу для розрахунків величин 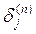шару n з величин 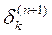більше старшого шару n+1

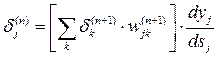. (7)

Для вихідного ж шару

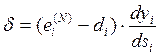. (8)

Тепер ми можемо записати (2) у розкритому вигляді:

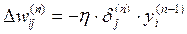. (9)

Іноді для надання процесу корекції ваг деякої інерційності, що згладжує різкі перегони при переміщенні по поверхні цільової функції, (9) доповнюється значенням зміни ваги на попередній ітерації

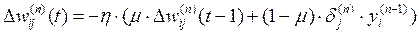, (10)

де μ – коефіцієнт інерційності,

t – номер поточної ітерації.

Таким чином, повний алгоритм навчання НМ за допомогою процедури зворотного поширення будується так:

1. Подати на входи мережі один з можливих образів і в режимі звичайного функціонування НМ, коли сигнали поширюються від входів до виходів, розрахувати значення останніх. Нагадаємо, що

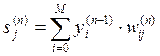, (11)

де M – число нейронів у шарі n–1 з урахуванням нейрона з постійним вихідним станом +1, що задає зсув; y_i^(n-1)=x_ij⁽ⁿ⁾ – i-ий вхід нейрона j шару n.

y_j⁽ⁿ⁾=f(s_j⁽ⁿ⁾), (12)

де f ( ) – сигмоїд.

y_q⁽⁰⁾=I_q, (13)

де I_q – q-а компонента вектора вхідного образу.

2. Розрахувати δ для вихідного шару по формулі (8).

Розрахувати по формулі (9) або (10) зміни ваг шару N.

3. Розрахувати по формулах (7) і (9) (або (7) і (10)) відповідно 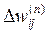і 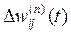для всіх інших шарів, n=N–1,...1.

4. Скорегувати всі ваги в НМ

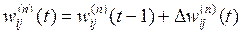. (14)

5. Якщо помилка мережі істотна, перейти на крок 1. У іншому випадку – кінець.

Мережі на кроці 1 почергово у випадковому порядку пред'являються всі тренувальні образи, щоб мережа, образно кажучи, не забувала одні по мірі запам'ятовування інших. Алгоритм ілюструється рисунком 2.

З виразу (9) видно, що коли вихідне значення y_i (n–1) прагне до нуля, ефективність навчання помітно знижується. При двійкових вхідних векторах у середньому половина вагових коефіцієнтів не буде коректуватися, тому область можливих значень виходів нейронів [0, 1] бажано зсунути в межі [–0.5, +0.5], що досягається простими модифікаціями логістичних функцій. Наприклад, сигмоїд з експонентою перетвориться до вигляду

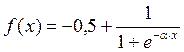. (15)

Тепер торкнемося питання ємності НМ, тобто числа образів, пропонованих на її входи, які вона здатна навчитися розпізнавати. Для мереж із числом шарів більше двох, воно залишається відкритим. Для НМ із двома шарами детерміністська ємність мережі C_d оцінюється так:

N_w/N_y<C_d<N_w/N_ylog(N_w/N_y), (16)

де N_w – число ваг, які підстроюють,

N_y – число нейронів у вихідному шарі.

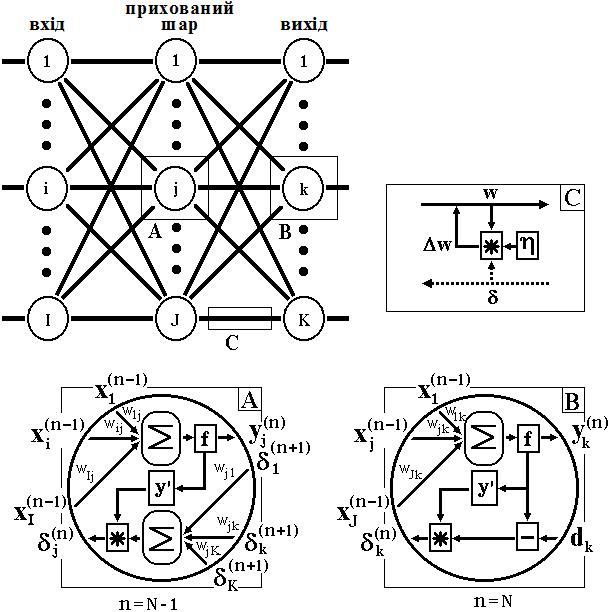
Рис. 2

Слід відзначити, що даний вираз отриманий з урахуванням деяких обмежень. Наприклад, N_w/N_y>1000. Однак вищенаведена оцінка виконувалася для мереж з активаційними функціями нейронів у вигляді порога, а ємність мереж із гладкими активаційними функціями, наприклад – (15), звичайно більша. Крім того, прикметник "детерміністська" означає, що отримана оцінка ємності підходить абсолютно для всіх можливих вхідних образів, які можуть бути представлені N_x входами. У дійсності розподіл вхідних образів, як правило, має деяку регулярність, що дозволяє НМ проводити узагальнення і, таким чином, збільшувати реальну ємність. Через те, що розподіл образів у загальному випадку заздалегідь не відомий, ми можемо говорити про таку ємність тільки приблизно, але звичайно вона разів у два перевищує ємність детерміністську.

У продовження розмови про ємності НМ логічно зачепити питання про необхідну потужність вихідного шару мережі, що виконує остаточну класифікацію образів. Справа в тому, що для поділу безлічі вхідних образів, наприклад, по двох класах досить усього одного виходу. При цьому кожен логічний рівень – "1" і "0" – буде позначати окремий клас. На двох виходах можна закодувати вже 4 класи і так далі. Однак результати роботи мережі, організованої таким чином, можна сказати – "під зав'язку", – не дуже надійні. Для підвищення вірогідності класифікації бажано ввести надмірність шляхом виділення кожному класу одного нейрона у вихідному шарі або, що ще краще, декількох, кожен з яких навчається визначати приналежність образа до класу зі своїм ступенем вірогідності, наприклад: високою, середньою й низькою. Такі НМ дозволяють проводити класифікацію вхідних образів, об'єднаних у нечіткі (розмиті або пересічні) множини. Ця властивість наближає подібні НМ до умов реального життя.

Розглянута НМ має трохи "вузьких місць". По-перше, у процесі навчання може виникнути ситуація, коли великі позитивні або негативні значення вагових коефіцієнтів змістять робочу точку на сигмоїдах багатьох нейронів в область насичення. Малі величини похідної від логістичної функції приведуть згідно із (7) і (8) до зупинки навчання, що паралізує НМ. По-друге, застосування методу градієнтного спуску не гарантує, що буде знайдений глобальний, а не локальний мінімум цільової функції. Ця проблема пов'язана ще з однією, а саме – з вибором величини швидкості навчання. Доказ збіжності навчання в процесі зворотного поширення засновано на похідних, тобто збільшення ваг і, отже, швидкість навчання повинні бути нескінченно малими, однак у цьому випадку навчання буде відбуватися неприйнятно повільно. З іншого боку, занадто великі корекції ваг можуть привести до постійної нестійкості процесу навчання. Тому в якості η, як правило, вибирається число менше 1, але не дуже маленьке, наприклад, 0.1, і воно, загалом кажучи, може поступово зменшуватися в процесі навчання. Крім того, для виключення випадкових влучень у локальні мінімуми іноді, після того як значення вагових коефіцієнтів застабілізуються, η короткочасно дуже збільшують, щоб почати градієнтний спуск із нової точки. Якщо повторення цієї процедури кілька разів приведе алгоритм у той самий стан НМ, можна більш-менш упевнено сказати, що знайдено глобальний максимум, а не якийсь інший.

Існує й інший метод виключення локальних мінімумів, а заодно й паралічу НМ, що полягає в застосуванні стохастичних НМ, але про це краще поговорити окремо.