Некоторые важные примеры приложений.

Пример 4.1. Рассмотрим задачу Коши для системы обыкновенных дифференциальных уравнений первого порядка вида

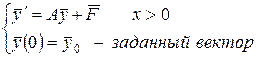(4.31)

где

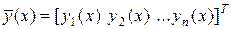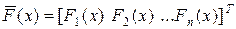; , (4.32)

причем 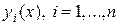– искомые функции; 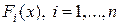– заданные функции; 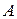– матрица, не зависящая от x.

Общее решение задачи (4.31) определяется формулой:

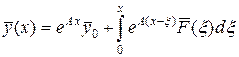. (4.32)

Пример 4.2. Рассмотрим задачу Коши для системы обыкновенных дифференциальных уравнений второго порядка вида

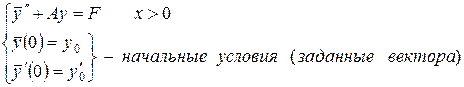(4.33)

Пусть 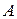– положительно определенная матрица, т.е. все ее собственные числа 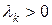. Тогда общее решение (4.33) можно записать в виде:

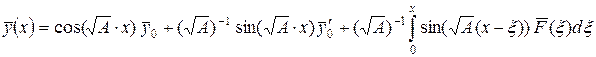. (4.34)

Пример 4.3. Рассмотрим задачу Коши для системы обыкновенных дифференциальных уравнений второго порядка вида

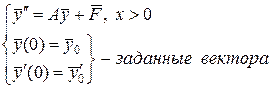(4.35)

Общее решение задачи (4.35) определяется формулой:

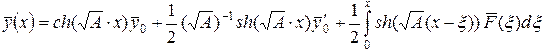, (4.36)

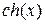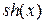где и – гиперболические синус и косинус от произвольного аргумента.