Классификация бинарных отношений.
ОТНОШЕНИЯ.
Понятие отношение является одним из фундаментальных понятий математики. Основы теории отношений заложили в конце XIX-го – начале XX–го столетий немецкий математик Е. Шредер и британские математики А. Уайтхед и Б. Рассел при разработке логического обоснования математики. В настоящее время отношения – это мощный аппарат, имеющий исключительное значение, как для современной математики, так и для ее многочисленных приложений. Отношение – это фундаментальное понятие в современной информатике. Действительно, повсеместно применяются реляционные (от английского слова relational, т.е. построенные на отношениях) системы управления базами данных (реляционная модель была разработана Е. Коддом в 1970 году). Более того, эффективность использования любого языка программирования или структур данных в процессе моделировании реальных ситуаций определяется, в конечном итоге, тем, насколько легко могут быть реализованы те или иные действия с отношениями.
Основные понятия и определения.
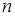 -арным отношением между элементами множеств
-арным отношением между элементами множеств 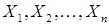 (взятыми в указанном порядке) называется любое подмножество множества
(взятыми в указанном порядке) называется любое подмножество множества 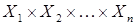 . Если
. Если 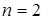 , то отношение – бинарное, а если
, то отношение – бинарное, а если 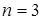 – то тернарное. В настоящем разделе отношения обозначаются строчными греческими буквами. При необходимости используются индексы.
– то тернарное. В настоящем разделе отношения обозначаются строчными греческими буквами. При необходимости используются индексы.
Пример 2.1. 1. Отношениями из окружающего нас мира (конечно, в каждом случае должно быть четко указано, между элементами каких множеств определено отношение) являются: 1) фирма 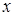 – поставщик сырья для фирмы
– поставщик сырья для фирмы 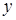 (бинарное отношение); 2) студенты
(бинарное отношение); 2) студенты 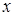 и
и 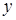 ДонНУ учатся в группе
ДонНУ учатся в группе 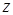 (тернарное отношение); 3) город
(тернарное отношение); 3) город 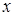 расположен севернее, чем город
расположен севернее, чем город 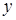 (бинарное отношение) и т.д.
(бинарное отношение) и т.д.
2. Отношениями из курса школьной математики являются:
1) бинарные отношения равенства 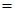 и порядка
и порядка 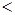 ,
, 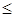 ,
, 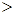 и
и 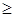 для чисел:
для чисел:
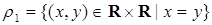 ,
, 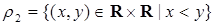 ,
,
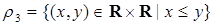 ,
, 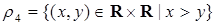 ,
,
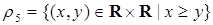 ;
;
2) бинарное отношение делимости для натуральных чисел:
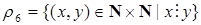 ;
;
3) тернарные отношения, соответствующие основным действиям арифметики:
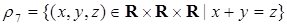 ,
, 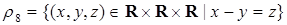 ,
,
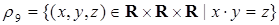 ,
, 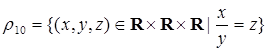 ;
;
4) бинарные отношения в планиметрии ( 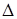 – множество всех треугольников на плоскости):
– множество всех треугольников на плоскости):
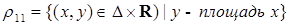 ,
,
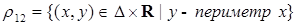 ,
,
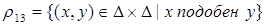 ;
;
и т.д.
3. В теории множеств (см. раздел 1) применяются бинарные отношения 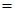 ,
, 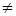 ,
, 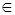 ,
, 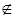 ,
, 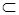 ,
, 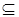 ,
, 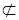 ,
, 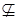 ,
, 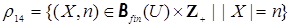 , где
, где 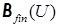 – множество всех конечных подмножеств множества
– множество всех конечных подмножеств множества 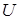 и т.д.
и т.д.
 Далее в настоящем разделе рассматриваются только бинарные отношения, т.е. отношения вида.
Далее в настоящем разделе рассматриваются только бинарные отношения, т.е. отношения вида. 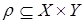 . Если утверждение
. Если утверждение 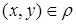 – истинное, то говорят, что элемент
– истинное, то говорят, что элемент 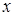 находится в отношении
находится в отношении  с элементом
с элементом 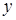 , а если утверждение
, а если утверждение 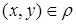 – ложное (т.е.
– ложное (т.е. 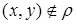 ) – что элемент
) – что элемент 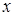 не находится в отношении
не находится в отношении  с элементом
с элементом 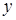 . Вместо записей
. Вместо записей 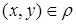 и
и 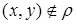 иногда пишут, соответственно,
иногда пишут, соответственно, 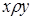 и
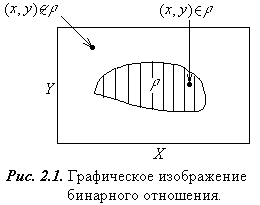
и 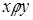 . Графическое представление декартового произведения двух множеств (см. рис. 1.3) дает возможность изобразить бинарное отношение
. Графическое представление декартового произведения двух множеств (см. рис. 1.3) дает возможность изобразить бинарное отношение 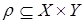 (рис. 2.1). При этом любая пара
(рис. 2.1). При этом любая пара 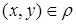 интерпретируется как координаты точки плоскости, представляющей соответствующий элемент множества
интерпретируется как координаты точки плоскости, представляющей соответствующий элемент множества  .
.
Образом элемента 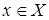 для отношения
для отношения 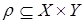 называется множество
называется множество
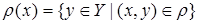 (
( 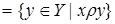 ) (2.1)
) (2.1)
( 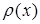 называется также проекцией элемента
называется также проекцией элемента 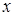 на множество
на множество 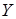 для отношения
для отношения  ). Прообразом элемента
). Прообразом элемента 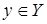 для отношения
для отношения  называется множество
называется множество
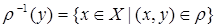 (
( 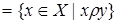 ) (2.2)
) (2.2)
 (
( 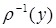 называется также проекцией элемента
называется также проекцией элемента 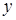 на множество
на множество 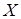 для отношения
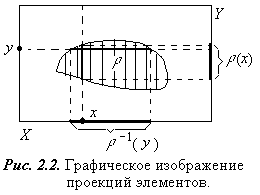
для отношения  ). Графическое изображение проекций элементов показано на рис. 2.2.
). Графическое изображение проекций элементов показано на рис. 2.2.
Пример 2.2. Для бинарных отношений 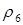 и
и 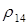 (см. пример 2.1) имеем: 1)
(см. пример 2.1) имеем: 1) 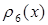
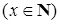 – это множество всех (положительных) делителей числа
– это множество всех (положительных) делителей числа 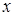 ; 2)
; 2) 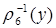
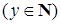 – это множество всех (положительных) кратных числа
– это множество всех (положительных) кратных числа 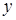 ; 3)
; 3) 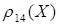
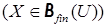 – это мощность множества
– это мощность множества 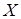 ; 4)
; 4) 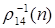
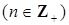 – это множество всех подмножеств универсального множества
– это множество всех подмножеств универсального множества 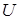 , содержащих в точности
, содержащих в точности 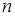 элементов.
элементов.
Множество
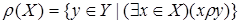 (2.3)
(2.3)
называется множеством значений отношения  , а множество
, а множество
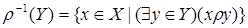 (2.4)
(2.4)
называется областью определения отношения  . Часто
. Часто 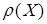 и
и 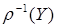 называют, соответственно, второй и первой проекциями отношения
называют, соответственно, второй и первой проекциями отношения  .
.
Пример 2.3. Пусть 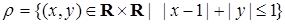 .
.
Тогда 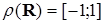 ,
, 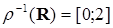 .
.
Классификация бинарных отношений.
Бинарное отношение 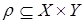 – функциональное, если
– функциональное, если 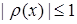 для всех
для всех 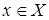 .
.
Пример 2.4. 1. Среди бинарных отношений из примера 2.1 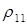 ,
, 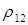 и
и 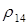 – функциональные отношения, а
– функциональные отношения, а 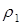 ,
, 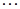 ,
, 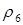 и
и 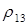 не являются функциональными.
не являются функциональными.
2. Бинарное отношение  из примера 2.3 не является функциональным.
из примера 2.3 не является функциональным.
Замечание 2.1. С функциональным отношением 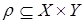 можно сопоставить (возможно, частичное) отображение
можно сопоставить (возможно, частичное) отображение 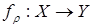 , определяемое равенством
, определяемое равенством
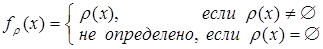 (
( 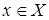 ).
).
Ясно, что 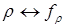 – взаимно-однозначное соответствие между множеством всех функциональных отношений
– взаимно-однозначное соответствие между множеством всех функциональных отношений 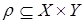 и множеством всех (возможно, частичных) отображений
и множеством всех (возможно, частичных) отображений 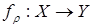 . Само функциональное отношение
. Само функциональное отношение 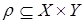 называется графиком отображения
называется графиком отображения 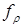 .
.
Функциональное отношение 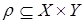 называется:
называется:
инъективным (или взаимно-однозначным), если образы различных элементов различны, т.е.
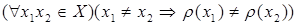 ;
;
сюръективным (или отношением на), если каждый элемент 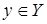 является образом хотя бы одного элемента
является образом хотя бы одного элемента 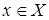 , т.е.
, т.е.
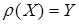 (
( 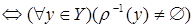 );
);
биективным, если оно является и инъективным, и сюръективным.
Пример 2.5. 1. Рассмотрим функциональные отношения 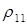 ,
, 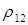 и
и 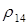 из примера 2.1. Отношения
из примера 2.1. Отношения 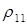 и
и 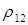 не являются ни инъективными (два различных треугольников могут иметь одинаковую площадь или периметр), ни сюръективными (площадь и периметр треугольника – положительные числа). Отношение
не являются ни инъективными (два различных треугольников могут иметь одинаковую площадь или периметр), ни сюръективными (площадь и периметр треугольника – положительные числа). Отношение 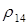 – инъективное тогда и только тогда, когда, либо
– инъективное тогда и только тогда, когда, либо 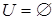 , либо
, либо 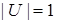 . Отношение
. Отношение 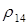 – сюръективное тогда и только тогда, когда
– сюръективное тогда и только тогда, когда 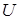 – бесконечное множество. Следовательно, ни одно из отношений
– бесконечное множество. Следовательно, ни одно из отношений 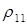 ,
, 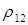 и
и 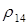 не является биективным.
не является биективным.
2. Определим бинарное отношение 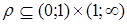 равенством
равенством
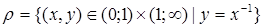 .
.
Для каждого не равного нулю числа существует единственное обратное ему число. Следовательно,  – функциональное отношение. Так как
– функциональное отношение. Так как
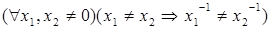 ,
,
то  – инъективное отношение. А так как
– инъективное отношение. А так как
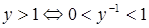 ,
,
то  – сюръективное отношение. Отношение
– сюръективное отношение. Отношение  одновременно является инъективным и сюръективным, т.е.
одновременно является инъективным и сюръективным, т.е.  – биективное отношение.
– биективное отношение.
Замечание 2.2. Если функциональное отношение 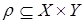 – инъективное, сюръективное или биективное, то отображение
– инъективное, сюръективное или биективное, то отображение 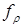 называется, соответственно, инъективным, сюръективным или биективным. Именно в последнем случае отображение
называется, соответственно, инъективным, сюръективным или биективным. Именно в последнем случае отображение 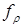 устанавливает взаимно-однозначное соответствием между множествами
устанавливает взаимно-однозначное соответствием между множествами 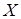 и
и 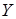 .
.
Дата добавления: 2015-10-09; просмотров: 2740;
