ИССЛЕДОВАНИЕ ВЛИЯНИЯ СТЕПЕНИ ЛЕГИРОВАНИЯ НА КОНТАКТНУЮ РАЗНОСТЬ ПОТЕНЦИАЛОВ И ШИРИНУ ОПЗ p-n ПЕРЕХОДА

Электронно-дырочным переходом (р - n переходом) называют контакт двух областей полупроводника с электронным (n-типа) и дырочным (р-типа) типом проводимости. В полупроводнике n-типа, легированном донорами основными носителями заряда являются электроны (nn- концентрация электронов), неосновными - дырки (рn- концентрация дырок).

Ионизированные атомы доноров (Nd+- концентрация доноров) чаще всего замещают места атомов основного вещества. В полупроводнике р - типа, легированном акцепторами присутствуют следующие заряды: дырки, являющиеся основными носителями заряда (рр), неосновные носители - электроны (nр) и неподвижные ионизированные атомы акцепторов (Na-).

Р - n переход является симметричным, если концентрация доноров в n-области равна концентрации акцепторов в р - области: N_d =N_a и несимметричным, если концентрации примесей неодинаковы.

Концентрация неосновных носителей n_p и р_n можно оценить из закона действующих масс, согласно которому в условиях термодинамического равновесия выполняется соотношение:

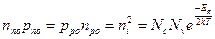(2.1)

где n_i - собственная концентрация носителей заряда, N_c, N_v - эффек­тивные плотности состояний зоны проводимостей и валентной зоны соответственно, зависящие от эффективных масс электронов и дырок, Е_g - ширина запрещенной зоны, k - постоянная Больцмана, Т - абсолютная температура.

Так как концентрация основных носителей, определяемая концентрацией примесей, существенно больше концентрации неос­новных носителей n_no>>p_no , p_po>>n_po, то в соответствии с (2.1) будут справедливы следующие соотношения n_no>>n_po, p_po>>p_no Все это означает, что на контакте между р- и n-областями имеет место градиент концентраций электронов и дырок (Рис.1), в результате чего возникает диффузионный ток электронов из n - области в р - область и обратный поток дырок из р - области в n - область.

n, p n, p

n_no p_po n_no

p_po

n_po

p_no n_po p_no

x x

d_n d_p d_n d_p

d

d

а) б)

Рис. 1.

а - симметричный переход (Nд=Nа), б - несимметричный переход' (Nд>Nа ).

При этом вблизи границы раздела n- и р- областей останется оголенный остов ионизированных примесей, которые создадут объемный положительный заряд в n-области и объемный отрицательный заряд в р- области. Эта лишенная подвижных носителей заряда приконтактная область с высоким сопротивлением называется областью пространственного заряда (ОПЗ) или областью истощенного слоя (рис.2).

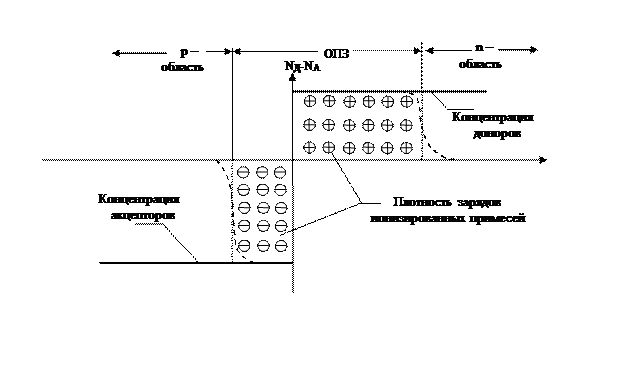
Рис. 2.

Заряды ионизированных примесей создают в ОПЗ электрическое поле, направленное так, что оно препятствует дальнейшему переходу через р-n переход основных носителей, в результата чего устанавливается равновесие.

Незначительное количество основных носителей, которым удается преодолеть электрическое поле ОПЗ уравновешивается потоком неосновных носителей, которые перебрасываются через р-n переход.

Наличие электрического поля в приконтактной области обуславливает разность потенциалов между р- и n-областями, которая называется контактной разностью потенциалов и может быть выражена через концентрации основных и неосновных носителей зарядов:

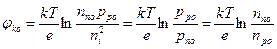(2.2)

Величина Е_ПО носит название высоты потенциального барьера:

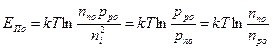(2.3)

На энергетической диаграмме р-n перехода существование контактной разности потенциалов проявляется в изгибе энергетических зон на величину ej_o, который

означает наличие энергетического барьера (рис.3) для перехода основных носителей заряда через р - n переход. При комнатной температуре n_n/n_p==10⁶ – 10²⁰, величина энергетического барьера ej_o составляет 0,35 - 1,2 эВ, то есть не превышает 1,4 эВ. Чтобы определить ширину ОПЗ d, нужно решить уравнение Пуассона при заданных граничных условиях. Для одномерного случая это уравнение имеет вид:

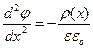(2.4)

E p

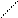
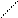n

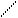
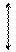
E_C Е_ПО= ej_o

E_F

E_g

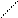
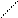
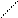
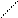
E_V

d_n d_o d_p E^|

Рис.3.

Решение уравнения определяется объемной плотностью заряда r(х) (рис.3). Для резкого симметричного перехода будем иметь для n- области

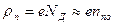, (2.5)

для р- области

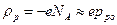, (2.6)

Граничные условия:

при х=d_n 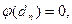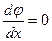(2.7)

при х=d_p 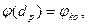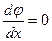(2.8)

Решая уравнение Пуассона при данных граничных условиях, получим следующие результаты:

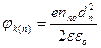, откуда 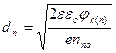(2.9)

где j_k(n) - доля контактной разности потенциалов, падающая на n-область, d_n - ширина ОПЗ в n - области,

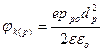, откуда 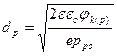, (2.10)

где j_k(p)- доля контактной разности потенциалов, падающая на р- область, d_p- ширина ОПЗ в р- области.

Полная контактная разность потенциалов р-n перехода равна j_k0=j_k(n) + j_k(p) , а полная ширина ОПЗ – d = d_n + d_p. Учитывая, что

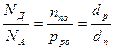(2.11)

окончательно получим

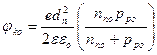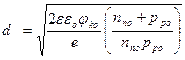, (2.12)

Из (2.12) видно, что толщина слоев объемных зарядов в n- и р- областях обратно пропорциональна концентрации основных носителей (степени легирования) в этих областях. Для симметричного перехода d_n=d_p, а для несимметричного ОПЗ располагается главным образом в менее легированном слое, т.е. можно считать, что для случая N_Д > N_A вся ОПЗ сосредоточена в р - области: d = d_p, и наоборот.

Более точное выражение для ширины ОПЗ получается если учесть кроме концентрации ионизированной примеси вклад основных носителей заряда, т.е. положить 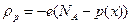в р – области перехода и 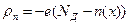для n – области. Ширина ОПЗ в таком приближении вычисляется по тем же формулам (2.9), (2.10) и (2.12), если j_k0 заменить на j_k0 – 2kT/e. Поправочный член 2kT/e появляется из-за наличия двух “хвостов” распределения основных носителей (штриховая линия на рис.2). Каждый из них вносит поправку kT/e. Сама поправка представляет собой просто дипольный момент неточности в распределении, равной разности между истинным распределением и распределением в резком р – n переходе. С учетом этого ширина ОПЗ может быть найдена:

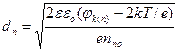; (2.13)

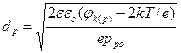; (2.14)

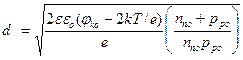. (2.15)

Для плавного р-n перехода с линейным распределением примеси N (х) = ах (рис.4) решение уравнения Пуассона приводит к другой зависимости ширины ОПЗ от j_o :

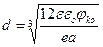(2.16)

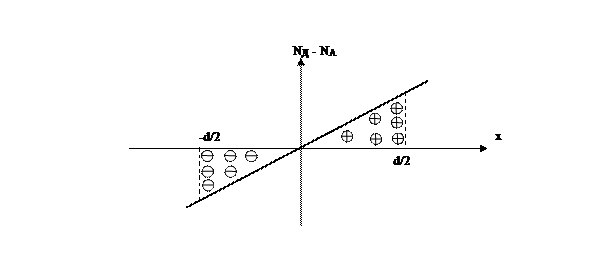
Рис.4.

Контактная разность потенциалов для плавного перехода пожет быть расчитана следующим образом:

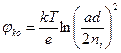
(2.17)