ИССЛЕДОВАНИЕ ВЛИЯНИЯ СТЕПЕНИ ЛЕГИРОВАНИЯ НА СВОЙСТВА ПРИМЕСНЫХ ПОЛУПРОВОДНИКОВ
Полупроводниковые материалы подразделяются на собственные и примесные. Чистый, свободный от примеси полупроводник называется собственным. На рис.1 показана структура такого полупроводника на основе кремния Si. В кристалле атомы кремния связаны друг с другом с помощью ковалентной связи, образованной за счет попарного обобществления валентных электронов. При температуре Т=0 К все электроны связаны с атомами кремния и в кристалле нет свободных электронов. В результате кремний при этой температуре является диэлектриком.
| | | |||||||||||||||||||||||||||||||||||||||
| | ||||||||||||||||||||||||||||||||||||||||
 |  |  |  | |||||||||||||||||||||||||||||||||||||
 |  |  |  | |||||||||||||||||||||||||||||||||||||
 |  | |||||||||||||||||||||||||||||||||||||||
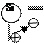 | ||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||
 |  | |||||||||||||||||||||||||||||||||||||||
 |  | |||||||||||||||||||||||||||||||||||||||
 |  | |||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||
 |  |  |  | |||||||||||||||||||||||||||||||||||||
 |  | |||||||||||||||||||||||||||||||||||||||
 |  | |||||||||||||||||||||||||||||||||||||||
 |  |  | ||||||||||||||||||||||||||||||||||||||
 |  |  | ||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||
 |  |  |  |  |  |  |  | |||||||||||||||||||||||||||||||||
 |  |  |  | |||||||||||||||||||||||||||||||||||||
 |  |  | ||||||||||||||||||||||||||||||||||||||
 |  |  | ||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||
Рис.1.
С ростом температуры происходит разрыв ковалентных связей. Появляется свободный электрон и незаполненная связь, которая называется дыркой. Дырка имеет по модулю такой же заряд, как и электрон, и является также свободным положительным зарядом способным перемещаться по кристаллу полупроводника.
Энергетическая диаграмма собственного полупроводника представлена на рис.2.

Рис.2.
Энергетический зазор между зоной проводимости и валентной зоной называется запрещенной зоной, ширина которой обозначается Eg.Ширина запрещенной зоныравна энергии, которая необходима для разрыва ковалентной связи. При температуре абсолютного нуля валентная зона полностью заполнена электронами, а зона проводимости свободна от них. В этом случае полупроводник ведет себя как диэлектрик, так как электропроводность равна нулю. С повышением температуры экспоненциально растет количество электронов способных преодолеть запрещенную зону и перейти из валентной в зону проводимости. В результате этого растет число свободных носителей заряда: электронов в зоне проводимости и дырок в валентной зоне. Данный процесс называется термогенерацией. Электропроводность материала при этом увеличивается. Концентрации электронов n и дырок p будут выражаться следующими формулами:
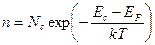 [м-3],
[м-3], 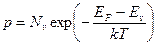 [м-3], (2.1)
[м-3], (2.1)
где: Ncи Nv- эффективные плотности состояний, соответственно, в зоне проводимости и в валентной зоне; ЕF- уровень Ферми; Ес- уровень "дна" зоны проводимости; Еv-уровень "потолка" валентной зоны; k - постоянная Больцмана; Т - абсолютная температура.
Эффективные плотности состояний для зоны проводимости и валентной зоны, соответственно, равны:
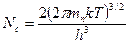 ,
, 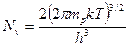 , (2.2)
, (2.2)
где mnи mp, соответственно, эффективные массы электрона и дырки.
Для расчета эффективных плотностей состояний удобно воспользоваться следующими приближенными формулами:

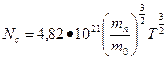 [м-3],
[м-3], 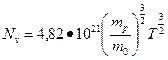 [м-3]
[м-3] 
Уровень Ферми есть энергетический уровень, вероятность заполнения которого носителями заряда равна 0,5. В собственном полупроводнике положение уровня Ферми определяется следующим образом:
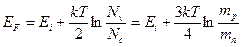 . [эВ] (2.3)
. [эВ] (2.3)
Исходя из (2.3), можно утверждать, что уровень Ферми в собственном полупроводнике лежит вблизи середины запрещенной зоны. Собственная концентрация носителей заряда может быть найдена из условий
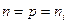 ,
, 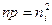 (2.4)
(2.4)
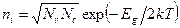 . (2.5)
. (2.5)
Равенство (2.4) носит название закона действующих масс. Уравнение (2.5) показывает, что собственная концентрация niпри заданной температуре определяется только шириной запрещенной зоны Eg.
Примесный полупроводник получается из собственного путем добавления в последний легирующей примеси. Для кремния и германия характерна примесь замещения, когда примесный атом замещает основной атом в узле кристаллической решетки. При использовании примеси пятой группы таблицы Менделеева, например мышьяка As, пятый валентный электрон примеси является слабосвязанным и отрывается от атома мышьяка уже при низкой криогенной температуре (рис.3). В результате образуются два типа зарядов: свободный электрон и неподвижный положительно заряженный ион примеси. Примесь такого типа называется донорной, а полупроводник - электронным или n-типа.
В полупроводнике n-типа, легированном донорами основными носителями заряда являются электроны (nn- концентрация электронов), неосновными - дырки (рn- концентрация дырок). В полупроводнике n-типа присутствуют также неподвижные положительно заряженные ионы донорной примеси (NД – концентрация донорной примеси).
 |  |  |  |  |  |  |  | |||||||||||||||||||||||||||||||||||||||||||||||
 |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||
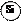 |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||
 |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||
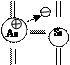 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||
 |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||
 |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||
 |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |  |  |  | |||||||||||||||||||||||||||||||||||||||||||||||||||
 |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||
 |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||
 |  |  | ||||||||||||||||||||||||||||||||||||||||||||||||||||
 |  |  | ||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |  |  |  |  |  |  |  | |||||||||||||||||||||||||||||||||||||||||||||||
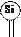 |  |  |  | |||||||||||||||||||||||||||||||||||||||||||||||||||
 |  |  | ||||||||||||||||||||||||||||||||||||||||||||||||||||
 |  |  | ||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Рис.3.
На рис.4 показана энергетическая диаграмма полупроводника n-типа. Энергетические уровни доноров лежат вблизи дна зоны проводимости Ес. Так как вероятность заполнения электронами зоны проводимости выше, чем вероятность заполнения дырками валентной зоны, то уровень Ферми в полупроводнике n-типа располагается вблизи дна зоны проводимости Ес.
 Еион
Еион














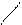
|
 Ес
Ес
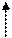









 ЕF
ЕF














 Еv
Еv
Рис.4.
Энергия ионизации примеси Еион равна энергии, которую необходимо затратить для того, чтобы оторвать пятый валентный электрон от атома донорной примеси.
При легировании собственного полупроводника элементами третьей группы таблицы Менделеева, например бором, для образования устойчивой связи в кристалле атому примеси не хватает одного электрона. Примесный атом заимствует недостающий электрон у соседних атомов кремния, разрывая ковалентную связь (рис.5). В результате образуются два типа зарядов: свободная дырка и неподвижный отрицательно заряженный ион примеси. Примесь такого типа называется акцепторной, а полупроводник – дырочным или р-типа.

 |  | ||||||||||||||||||||||||||||||||||||||||||||
 |  | ||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||
 |  | ||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||
 |  | ||||||||||||||||||||||||||||||||||||||||||||
 |  | ||||||||||||||||||||||||||||||||||||||||||||
 |  |  | |||||||||||||||||||||||||||||||||||||||||||
 |  | ||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||
 |  |  | |||||||||||||||||||||||||||||||||||||||||||
 |  | ||||||||||||||||||||||||||||||||||||||||||||
 |  | ||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||
 |  |  |  |  |  | ||||||||||||||||||||||||||||||||||||||||
 |  | ||||||||||||||||||||||||||||||||||||||||||||
 |  | ||||||||||||||||||||||||||||||||||||||||||||
 |  |  | |||||||||||||||||||||||||||||||||||||||||||
 |  |  | |||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||
 |  |  |  |  |  |  |  | ||||||||||||||||||||||||||||||||||||||
 |  |  |  | ||||||||||||||||||||||||||||||||||||||||||
 |  |  | |||||||||||||||||||||||||||||||||||||||||||
 |  |  | |||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||







Рис.5.
На рис.6 показана энергетическая диаграмма полупроводника р-типа. Энергетические уровни доноров лежат вблизи потолка валентной зоны Еv. Так как вероятность заполнения дырками валентной зоны выше, чем вероятность заполнения электронами зоны проводимости, то уровень Ферми в полупроводнике р-типа располагается вблизи потолка валентной зоны Еv.














 Ес
Ес
 |
|
 ЕF
ЕF
























 Еv
Еv
Еион
Рис.6.
В полупроводнике р - типа, легированном акцепторами присутствуют следующие заряды: дырки, являющиеся основными носителями заряда (рр), неосновные носители - электроны (nр) и неподвижные ионизированные атомы акцепторов (Na).
В составном полупроводнике, например в GaAs, примесь также является замещающей. Так замещение элемента III группы (Ga) примесью II группы (Zn,Cd,Hg) приводит к проводимости р-типа. Цинк Zn, например, захватывает один электрон от основного материала для образования устойчивой связи в кристаллической решетке с атомами мышьяка As. Элементы VI группы (S,Se,Te), замещая элемент V группы (As), по тем же причинам действуют как доноры.
Концентрация неосновных носителей np и рn можно определить из закона действующих масс, согласно которому в условиях термодинамического равновесия выполняется соотношение:
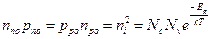 (2.7)
(2.7)
где ni - собственная концентрация носителей заряда, Nc, Nv - эффективные плотности состояний зоны проводимостей и валентной зоны соответственно, зависящие от эффективных масс электронов и дырок, Еg - ширина запрещенной зоны, k - постоянная Больцмана, Т - абсолютная температура.
Концентрации электронов и дырок в примесных полупроводниках будут в сильной степени зависеть от температуры Т. В общем случае концентрации основных носителей заряда будут равны:


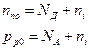 (2.8)
(2.8)
При низких криогенных температурах собственная концентрация ni мала, при этом примесь ионизирована лишь частично. Этому случаю соответствует область примесной проводимости I (рис.7).


Рис.7.
Наклон зависимости в этой области пропорционален энергии ионизации примеси Еион.
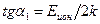 (2.9)
(2.9)
По мере роста температуры примесь истощается и при температуре истощения примеси Тs все атомы примеси полностью ионизированы. Температура истощения примеси Тs может быть найдена из следующего выражения:
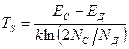 (2.10)
(2.10)
для р-типа 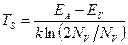
В области II, называемой областью истощения примеси, концентрация основных носителей заряда меняется слабо. В этой области ее можно принять равной концентрации примеси:
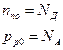 (2.11)
(2.11)
Положение уровня Ферми для этого случая определяется из соотношения:
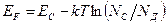 (2.12)
(2.12)
для р-типа 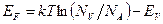
С ростом температуры будет возрастать собственная концентрация носителей заряда ni и концентрация основных носителей заряда будет определяться (2.8). При достижении некоторой температуры называемой температурой ионизации Тi собственная концентрация ni начнет превышать примесную: ni>NД. Область III , в которой это имеет место, называется областью собственной проводимости. Полупроводник из примесного превращается в собственный.
Температура ионизации может быть выражена следующим образом:
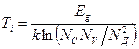 (2.13)
(2.13)
для р-типа 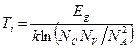
В этой области наклон температурной зависимости прямо пропорционален ширине запрещенной зоны Еg:
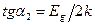 (2.14)
(2.14)
| <== предыдущая лекция | | | следующая лекция ==> |
| Приложение 4 | | | ИССЛЕДОВАНИЕ ВЛИЯНИЯ СТЕПЕНИ ЛЕГИРОВАНИЯ НА КОНТАКТНУЮ РАЗНОСТЬ ПОТЕНЦИАЛОВ И ШИРИНУ ОПЗ p-n ПЕРЕХОДА |
Дата добавления: 2015-10-09; просмотров: 3627;
