Свободные колебания
Свободные колебания – колебания, протекающие в системе под действием её внутренних сил. Свободные колебания протекают около положения устойчивого равновесия системы. В реальных системах из-за действия сил сопротивления все свободные колебания являются затухающими. Если силы сопротивления велики, то свободные колебания в такой системе не возникают.
Если силы сопротивления можно считать равными нулю, то амплитуда свободных колебаний остается постоянной согласно закону сохранения полной механической энергии. В этом случае энергию колебательной системы можно рассчитать тремя способами:
1) через максимальное значение кинетической энергии;
2) через максимальное значение потенциальной энергии;
3) через сумму кинетической и потенциальной энергии в любой момент времени.
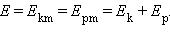
Рассмотрим две простейшие механические колебательные системы, в которых возможны свободные колебания.
Математический маятник – материальная точка на невесомой нерастяжимой нити в поле тяжести. Период колебаний математического маятника для небольшого угла отклонения от положения равновесия определяется по формуле:
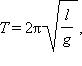
где l – длина нити, g – ускорение свободного падения.
Пружинный маятник – груз, на который действует только сила упругости. Период колебаний пружинного маятника определяется по формуле:
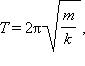
где m – масса груза, k – жёсткость пружины.
Если на пружинный маятник действует постоянная внешняя сила, то она лишь смещает положение равновесия системы и не влияет на характеристики колебательного движения. Например: период колебаний груза на вертикальной пружине в гравитационном поле определяется по формуле пружинного маятника, так как внешняя сила – сила тяжести – постоянна.
Дата добавления: 2015-10-09; просмотров: 742;
