Гармонические колебания
 Механические колебания – механическое движение с периодическим изменением направления на противоположное.
Механические колебания – механическое движение с периодическим изменением направления на противоположное.
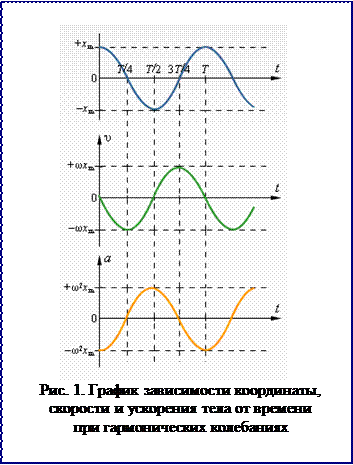
Гармонические колебания – колебания, при которых физические величины, описывающие систему, изменяются во времени по гармоническому закону (по закону синуса или косинуса). Например, координата материальной точки, совершающей гармоническое колебание, может быть описана уравнением:
x = xm cos (ωt + φ0),
где xm – амплитуда колебания, ω – циклическая частота, φ0 – начальная фаза. На рисунке показано гармоническое колебание, протекающее по закону косинуса, с начальной фазой, равной нулю.
Амплитуда – максимальное смещение тела от положения равновесия.
Фаза – выражение, стоящее под гармонической функцией.
φ = ωt + φ0; [φ] = рад.
Период – минимальный промежуток времени, в течение которого колебательный процесс полностью повторяется. Для вычисления периода определяется количество повторений процесса за некоторый интервал времени.
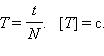
Период показывает время одного полного процесса.
Частота – величина, обратная периоду.
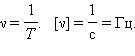
Частота показывает число повторений процесса за единицу времени.
Циклическая частота – величина, в 2π раз превышающая частоту.
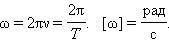
Гармоническая функция обладает следующим свойством: вторая производная гармонической функции прямо пропорциональна этой же функции, взятой с противоположным знаком. Найдём вторую производную по времени координаты, меняющейся по закону косинуса:
x = xm cos (ωt0);
x′ = υm = xmω sin (ωt) = υm sin (ωt);
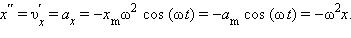
Дата добавления: 2015-10-09; просмотров: 745;
