Классификация прямоугольных аксонометрических проекций

Коэффициенты (показатели) искажения могут быть определены следующим образом:

Коэффициенты (показатели) искажения по аксонометрическим осям равны косинусам углов d наклона координатных осей к плоскости аксонометрических проекций.

Если все три показателя равны между собой, т.е. если координатные оси наклонены к плоскости аксонометрических проекций под одинаковым углом, то такая аксонометрия называется изометрия.

.K_x = K_y = K_z

Определим величину показателей искажения. Для изометрии равенство

K²_x + K²_y + K²_z = 2

запишется так

3K²_x = 2,

Откуда

K_x = 0,82

Аксонометрические оси X⁰, Y⁰, Z⁰ в прямоугольной изометрии образуют между собой равные углы в 120⁰.

Если при построении прямоугольной изометрии учитываются показатели искажения по осям x, y, z и ониравны между собой K_x = K_y = K_z = 0,82,то такая аксонометрия называется нормальной или точной

Положение аксонометрических осей приведено на рис.1.

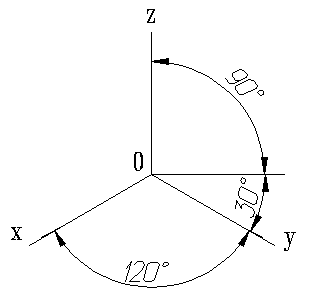
Рис 1.

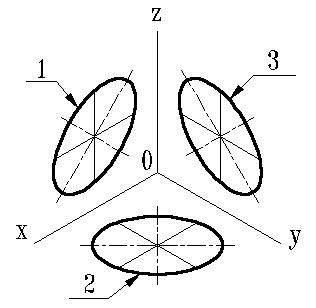
Рисунок 2. Окружность в изометрии
1-эллипс (большая ось расположена под углом 90⁰ к отсутствующей оси, т.е. y, а малая ось вдоль отсутствующей оси y в плоскости XOZ );
2-эллипс (большая ось расположена под углом 90⁰ к отсутствующей оси, т.е. z, а малая ось вдоль отсутствующей оси z y в плоскости XOY );
3-эллипс (большая ось расположена под углом 90⁰ к отсутствующей оси, т.е. x, а малая ось вдоль отсутствующей оси x y в плоскости YOZ).

Изометрическую проекцию для упрощения, как правило, выполняют без искажения по осям x, y, z, т.е. приняв коэффициент искажения равным 1, то такая аксонометрия называется приведенной, т.е. увеличенной в 1/0,82 = 1.22 раза. Она должна иметь обозначение на чертеже «Изометрия (1.22:1)».

Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются на аксонометрическую плоскость проекций в эллипсы (рис.2)
Если аксонометрическую проекцию выполняют без искажения по осям x, y, z, то большая ось эллипсов 1,2, 3 равна 1,22, а малая ось - 0.71 диаметра окружности.
Если аксонометрическую проекцию выполняют с искажением по осям x, y, z, то большая ось эллипсов 1, 2, 3 равна диаметру окружности, а малая - 0.58 диаметра окружности, то такая аксонометрия называется точной. Она никаких дополнительных обозначений на чертеже не имеет.

На рис.3 представлена деталь технической формы для построения изометрии.

Построение изометрии начинается с анализа структуры поверхностей детали. Известно из начертательной геометрии, что поверхность содержит элементы: образующие и направляющие, которые в разделе компьютерная графика называют примитивами вывода: ломаная линия, как частный случай, отрезок прямой и полигональная область, т.е. замкнутый выпуклый многоугольник. Рассматривая изображение, как структуру, заметим, что на фронтальной плоскости проекций направляющая каждого элемента (ромб, шестигранник, окружность, прямоугольник) представлены в проецирующим положении.

Каждое такое проецирующее положение на изометрии представим пересечением осей X иY. Базовое положение осей отметим цифрами 0,1, т.е. нижнее и верхнее положение направляющих детали, а дополнительное положение осей X иY отметим цифрами 2, 3, 4, 5, 6. В точке 0 направляющая внешней поверхности представлена прямоугольником, а направляющая внутренней поверхности представлена ромбом. В точке 1 направляющая внешней поверхности представлена шестигранником, а направляющая внутренней поверхности представлена ромбом.

На рис.4 представлены изометрические оси всех элементов направляющих детали технической формы в проецирующем положении. На уровне 1 изображены элементы шестигранника внешней поверхности и ромба внутренней поверхности. На уровне 1 вдоль оси X изображены узлы (точки) 1.1, 1.2 (1 цифра - № уровня, 2 цифра - № точки), через которые проведены линии параллельные оси Y. Вдоль оси Y и линиям им параллельным изображены узлы 1.3, 1.4, 1.5, 1.6, 1.7 элементы шестигранника внешней поверхности, размеры которых взяты с горизонтальной плоскости проекций чертежа, представленного на рис.3. Вдоль осей X и Y отмечены узлы 1.8, 1.9, 1.10, 1.11 элементы ромба внутренней поверхности детали. На 4 уровне обозначено нижнее положение внешней поверхности шестигранника узлами 4.1 – 4.7 на оси Y и линиям ей параллельным соответственно. На 0 уровне обозначено нижнее положение внутренней поверхности ромба узлами 0.8 – 0.11 на оси X и оси Y соответственно.

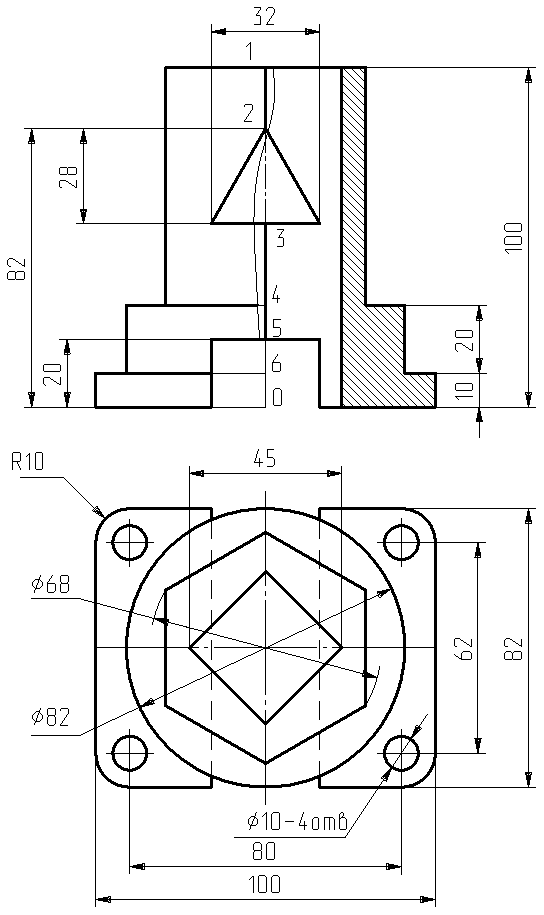
Рис.3

Соединяя образующими соответствующие узлы, получим внешнюю поверхность шестигранника, при этом образующие 1.1-4.1, 1.4-4.4, 1.6-4.6, 1.7-4.7 создают видимые грани внешней поверхности шестигранника.

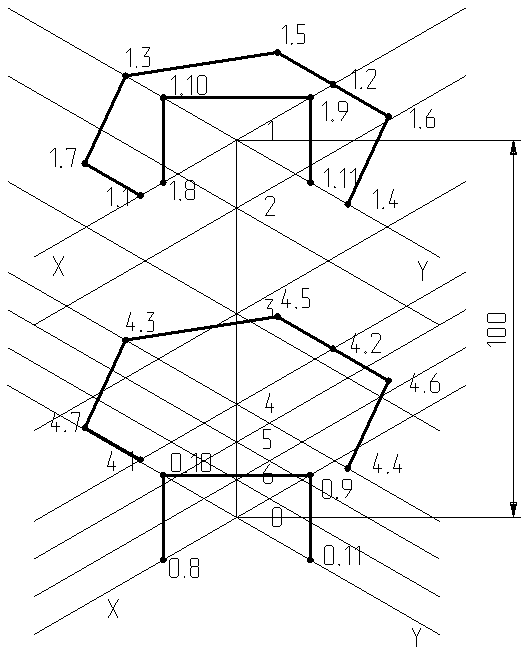
Рис.4

Соединяя образующими соответствующие узлы, получим внутреннюю поверхность ромба, при этом образующие 0.8-1.8, 0.11-1.11 создают видимые грани внутренней поверхности ромба выреза детали.

На рис.5 изображены элементы цилиндрической наружной поверхности, начальная направляющая которой отображена на уровне 4, а конечная направляющая на уровне 6 с вырезом по осям X иY. В соответствии с ГОСТ 2.317 – 69 эллипс представлен 8 точками, величины отрезков представлены по осям X иY в разные стороны от точки пересечения осей, равными радиусу окружности (R = 41мм), по перпендикуляру к отсутствующей оси (т.е. оси Z) величиной 1,22R, а вдоль отсутствующей оси - величиной 0,71R.

Точки, представленные на перпендикулярах к оси Z величиной 1.22R, на уровнях 4 и 6 формируют очерковые образующие цилиндрической поверхности, которые разделяют поверхность на видимые и не видимые участки. Очерковые образующие цилиндрической поверхности на рис.3 представлен углом 45⁰ с горизонтальной осью. На уровне 4 очерковые образующие шестигранной поверхности создают видимые и не видимые участки цилиндрической поверхности.

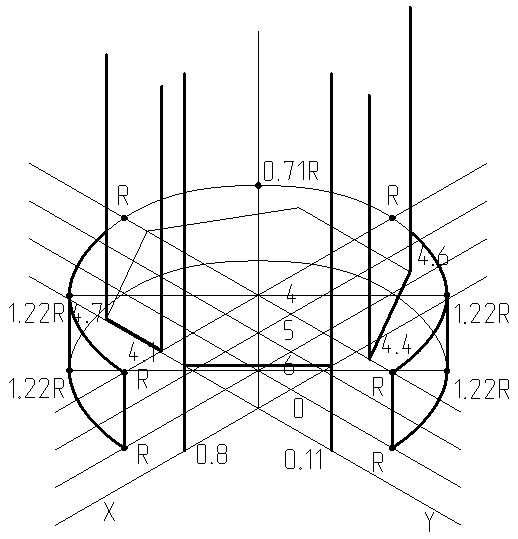
Рис.5

На уровнях 6 и 0 изобразим направляющую поверхности в виде прямоугольника с отверстиями и округление ребер и вырезом вдоль осей X иY. Изображение представим на рис.6. На уровнях 6 и 0 вдоль осей X иY проведем отрезки прямых с координатами X =50мм, Y =41мм в абсолютных величинах шага курсора. По координатам X =40мм, Y =31мм в абсолютных величинах шага курсора отобразим центра окружностей, диаметр которых равен 10мм, а также радиусы округления, равные R = 10мм, ребер прямоугольной плиты основания детали. В соответствии с ГОСТ 2.317 – 69 эллипс представлен 8 точками, величины отрезков представлены по осям X иY в разные стороны от точки пересечения осей, равными радиусу окружности (R = 5мм), по перпендикуляру к отсутствующей оси (т.е. оси Z) величиной 1,22R, а вдоль отсутствующей оси - величиной 0,71R. Аналогичным образом отобразим эллипс округления ребра (R = 10мм). Не видимые участки поверхности прямоугольной плиты на чертеже не указаны.

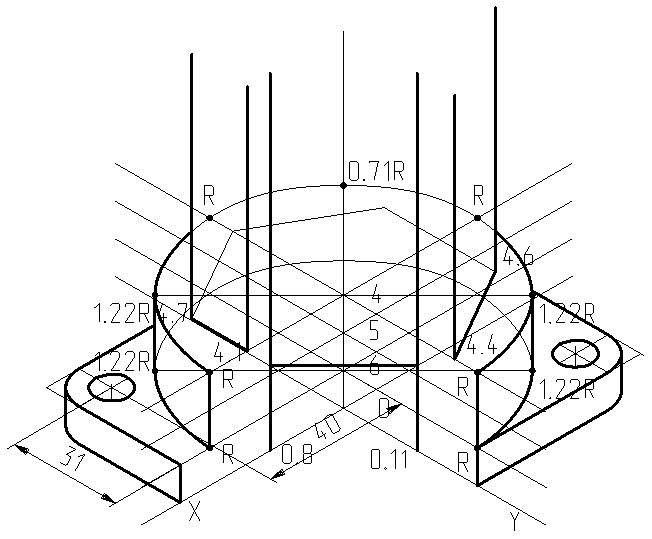
Рис. 6

Соединим построенные направляющие и образующие всех элементов детали между собой. Получим чертеж, представленный на рис.7

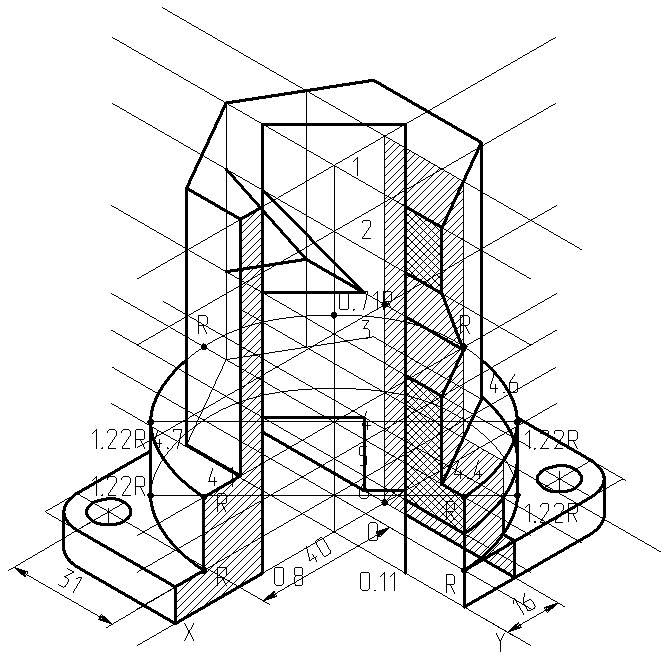
Рис.7

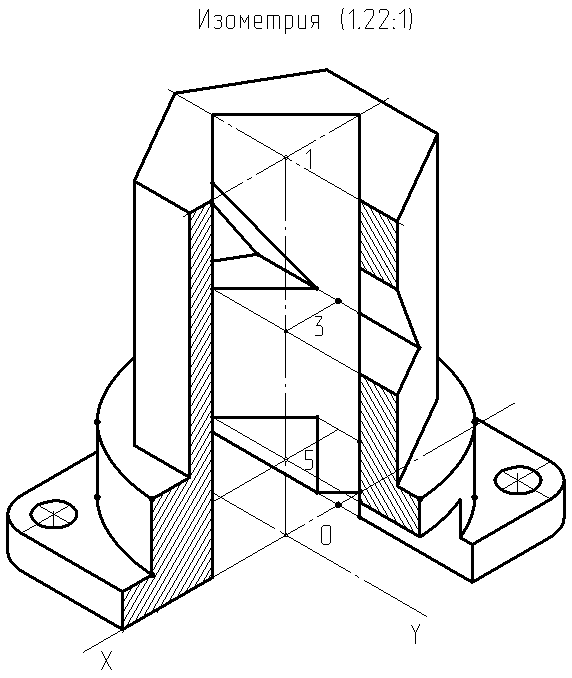
Рис.8