Теория метода и описание установки

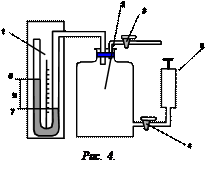
Экспериментальная установка состоит из стеклянного баллона 2(рис.4), соединенного с манометром 1 и насосом 5. Посредством крана 3баллон 2 может быть соединен с атмосферой. Давление в манометре h определяется по разности уровней жидкости левого колена 6 и правого колена 7.

Давление, установившееся в баллоне,

p₁=H+h₁,

где Н– атмосферное давление, h₁ – атмосферное давление, измеряемое разностью уровней жидкости в манометре 1.

Таким образом, состояние воздуха внутри баллона, которое назовем первым состоянием, будет характеризоваться параметрами: P₁=H+h₁; v; Т₁. Этому состоянию газа соответствует точка 1 рис.5. Затем открываем на короткое время кран 3(рис.4), соединяем баллон с окружающей средой. Этот процесс расширения можно считать адиабатическим.

Давление в сосуде устано­вится равным атмосферному P₂= Н, температура понизится до Т₂<Т₁, а объем будет равен V₂. Следовательно, в конце адиабати­ческого процесса у воздуха в бал­лоне будут параметры H; V₂; T₂(T₂ < T₁) (рис.5 точка 2).

Переход из первого состояния во второе является адиабатиче­ским, к такому переходу приме­ним уравнение Пуассона

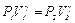. (14)

Через три–четыре минуты по­сле закрытия крана воздух в баллоне нагреется изохорически до комнатной температуры t₁, а давление повысится до Р₃ = H+h₂ (точка 3 на рис.5) h₂–разность уровней в манометре, когда температура в баллоне стала равной комнатной. Сравнивая конечное состояние «3» с первоначальным состоянием «1», видим, что они принадлежат одной и той же изотерме.

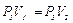(15)

Возведем (15) в степень g, получим 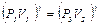и разделим его на (14): 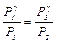прологарифмируем – 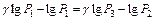, отсюда 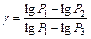. Принимая во внимание, что Р₁=H+h₁, P₂=H,P₃=H+h₂, т.е. давления мало отличаются друг от друга, разность логарифмов можно принять пропорциональной разностям самих давлений и

,

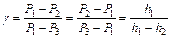откуда

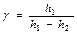. (16)

Последняя формула – рабочая.