Подбор параметра. Решается уравнение вида f(x)=0
Решается уравнение вида f(x)=0. Вопрос о нахождении приближённого решения распадается на 2 этапа:
· нахождение интервала изоляции корня (если он не задан)
· уточнение корня
Пример 4. Найти приближённое решение уравнения 8х3 - 17х2 + 8,5х - 8,25 = 0
методом подбора параметра. Решить уравнение графически, сравнить результаты.
Это уравнение имеет либо 3, либо 1 действительный корень.
Нахождение интервала изоляции корня(см. рис. 6):
| A | B | C | D | |
| x | y | корень | пoгрешность | |
| -8,25 | 1,851961 | 8,8293E-06 | ||
| 0,5 | -7,25 | |||
| -8,75 | ||||
| 1,5 | -6,75 | |||
| 4,75 | ||||
| 2,5 | 31,75 | |||
| 80,25 |
Рис.6.Приближённое решение нелинейного уравнения
· в области определения функции выбрать произвольным образом диапазон изменения х, например [0;3] с шагом 0,5. Заполнить значениями столбец х.
· заполнить значениями столбец Y=f(x):
B2← =8*A2^3-17*A2^2+8,5*A2-8,25
Скопировать формулу на диапазон В3:В8.
· выбрать отрезок, на концах которого функция принимает значения разных знаков, это и будет интервал изоляции корня. В нашем случае это [1,5; 2]. Если такого отрезка нет, то изменим диапазон изменения аргумента.
Уточнение корня:
· в качестве начального приближения к корню выбираем значение из отрезка [1,5; 2], пусть х0=1,7;
С2 ← 1,7
· вычисляем значение функции в этой точке, т.е. f(х0);
D2 ← =8*С2^3-17*С2^2+8,5*С2-8,25
· уточним это значение с помощью команды пункта меню
Сервис → Подбор параметра
В окне диалога:
Установить в ячейке ввести D2
Значение ввести 0
Изменяя значение ячейки ввести $C$2 (щелчёк на ячейке С2), ОК
Приближённое значение к корню находится в ячейке С2, х ≈ 1,851961. в ячейке D2 — погрешность корня 8,8293Е-0,6.
Графический способ решения уравнения:
Построить график функции Y=8х3 - 17х2 + 8,5х - 8,25 на отрезке [1,5; 2]
| x | y | 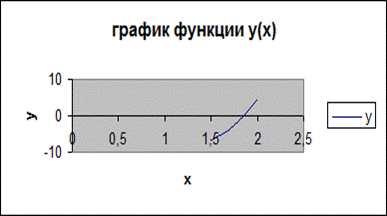
| ||||||
| 1,5 | -6,75 | |||||||
| 1,55 | -6,1265 | |||||||
| 1,6 | -5,402 | |||||||
| 1,65 | -4,5705 | |||||||
| 1,7 | -3,626 | |||||||
| 1,75 | -2,5625 | |||||||
| 1,8 | -1,374 | |||||||
| 1,85 | -0,0545 | |||||||
| 1,9 | 1,402 | |||||||
| 1,95 | 3,0015 | |||||||
| 4,75 | ||||||||
Значение корня х ≈ 1,8
Дата добавления: 2015-10-05; просмотров: 780;
