Требования к отбору факторов

Несмотря на то, что парная линейная регрессия легко интерпретируется, в действительности она встречается очень редко, поэтому более широкое применение получила множественная регрессия. Парная регрессия может дать хороший результат при моделировании, если влиянием других факторов, воздействующих на объект исследования, можно пренебречь. Но поведение отдельных экономическихпеременных контролировать нельзя, т.е. равенство всех прочих условий для оценки влияния одного исследуемого фактора обеспечить не удается. В этом случае следует попытаться выявить влияние других факторов, введя их в модель. Естественным продолжением парной линейной регрессии является множественная линейная регрессионная модель с р переменными:

y = a +b₁x₁ + b₂x₂ + … + b_px_p + ε

Каждый фактор x_i представляет собой набор из п наблюдений по одному и тому же признаку. Коэффициенты b_i - это частные производные у по факторам x_i:

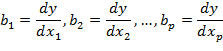
при условии, что все остальные факторы постоянны.

Главная цель множественного регрессионного анализа заключается в построении модели с большим числом факторов и определении при этом влияния каждого из них в отдельности, а также их совокупности на моделируемый показатель.

Модель линейной множественной регрессии, для которой выполняются условия Гаусса - Маркова, называется нормальной линейной множественной регрессией. Приступая к построению множественной регрессии, исследователь в самом начале сталкивается с проблемами отбора факторов, которые будут учитываться в регрессионном уравнении, и выбором его вида. При отборе факторов существуют определенные правила, выполнение которых необходимо, иначе оценки параметров уравнения и оно само будут недостоверными и не отразят истинную связь результативного признака с факторными.

Факторы должны отвечать следующим требованиям:

1.Факторы должны быть количественно измеряемы. Если модель необходимо включить качественный фактор, не имеющий количественной меры, то ему нужно придать количественную определенность (например, в модели урожайности качество почвы задается в виде баллов; в модели стоимости объектов недвижимости учитывается место ее нахождения: районы могут быть проранжированы), наличию или отсутствию какого-либо признака также должно придаваться числовое значение (например, мужчина - 0, женщина - 1).

2. Каждый фактор должен быть достаточно тесно связан с результатом (т.е. коэффициент парной линейной корреляции между каждым включаемым в модель фактором и результатом должен отличаться от нуля, причем на достаточно большую величину, что требуется для подтверждения наличия связи).

3.Факторы не должны быть тесно связаны между собой и тем более находиться в строгой функциональной связи (не должны коррелировать друг с другом).

Если между факторами существует высокая корреляция, то нельзя определить непосредственно влияние каждого из них на результативный показатель, и параметры уравнения регрессии оказываются неинтерпретируемыми.

Отбор факторов для включения в модель обычно осуществляется в два этапа: на первом подбираются факторы в зависимости от экономической сущности проблемы (т.е. набор факторов определяется непосредственно самим исследователем), а на втором на основе матрицы парных коэффициентов корреляцииустанавливается теснота связи для параметров регрессии.

Считается, что две переменные явно коллинеарны, т.е. линейно зависимы друг от друга, если rx_ix_j≥0,7. Если факторы явно коллинеарны, то они дублируют друг друга, и один из них рекомендуется исключать из регрессии. Особенность исключения фактора состоит в том, что предпочтение отдается не более тесно связанному с результатом, а тому, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами, включаемыми в модель. В требовании проявляется специфика множественной регрессии как метода исследования совокупного воздействия факторов в условиях их независимости друг от друга.

Однако матрица парных коэффициентов корреляции позволяет проследить лишь явную связь между факторами (попарно). Намного сложнее установить так называемую мультuколлuнеарность факторов, когда более чем два из них связаны между собой нестрогой линейной зависимостью. В связи с этим наибольшие трудности встречаются, когда необходимо выявить совокупное воздействие нескольких факторов друг на друга. Если при исследовании модели приходится сталкиваться с мультиколлинеарностью, то это означает, что некоторые из включаемых в модель факторов всегда будут действовать вместе.

На практике о наличии мультиколлинеарности судят по определителю матрицы парной межфакторной корреляции.

Предположим, что модель имеет следующий вид:

y = a +b₁x₁ + b₂x₂ + b₃x₃ + ε.

Построим для нее матрицу парной межфакторной корреляции и найдем ее определитель:

r_х1х1 r_х1х2 r_х1х3

Det ІRІ = r_х2х1 r_х2х2 r_х2х3

r_х3х1 r_х3х2 r_х3х3

Если факторы вообще не коррелируют между собой, то определитель данной матрицы равняется единице, так как в этом случае:

r_х1х1 = r_х2х2 = r_х3х3 = 1;

r_хiхj = r_хjхi ;

r_х1х2 = r_х1х3 = r_х2х3 = 0,

и матрица единична, поскольку все недиагональные элементы равны нулю:

1 0 0

Det ІRІ = 0 1 0 = 1.

0 0 1

Если же наоборот, между факторами существует полная линейная зависимость и все коэффициенты корреляции равны единице, то определитель такой матрицы равен нулю:

1 1 1

Det ІRІ = 1 1 1 = 0.

1 1 1

Можно сделать вывод, что чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И наоборот, чем ближе к единице определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.

При наличии явной мультиколлинеарности в модель следует включать не все факторы, а только те, которые в меньшей степени влияют на мультиколлинеарность (при условии, что качество модели снижается при этом незначительно). В наибольшей степени «ответственным» за мультиколлинеарность будет тот признак, который теснее связан с другими факторами модели (имеет более высокие по модулю значения коэффициентов парной линейной корреляции).

При отборе факторов также рекомендуется соблюдать следующее правило: число включаемых в модель факторов должно быть в шесть-семь раз меньше объема совокупности, по которой строится регрессия.