Метод Гаусса решения систем линейных уравнений

Сущность метода Гаусса заключается в том, что с помощью элементарных преобразований расширенная матрица системы (2.1) приводится к ступенчатому виду (элементарные преобразования производятся при этом только над строками матрицы). Причем выделяют две стадии метода Гаусса: прямой ход, когда мы «обнуляем» элементы под «диагональными» элементами, и обратный ход, когда мы «обнуляем» элементы над «диагональными». Если ранг матрицы r меньше числа неизвестных n, то необходимо выделить базисный минор матрицы системы. Тогда столбцы, из которых выделяется базисный минор, будут определять базисные переменные, а оставшиеся – свободные переменные. Более подробно алгоритм метода Гаусса заключается в следующем.

Рассмотрим систему (2.1) и расширенную матрицу данной системы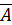

= ,

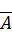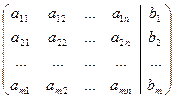Предположим, что элемент 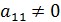. Если это не так, то перестановкой строк можно добиться, чтобы 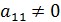. Разделим первую строку на 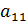, тогда новый элемент 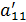=1. Далее по очереди обнуляем все элементы первого столбца, кроме первого. Чтобы получить ноль в первом элементе второй строки, умножаем первую строку на 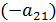и складываем со второй. Далее умножаем первую строку на 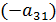и складываем с третьей и т.д. Получим

=

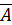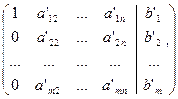
Для системы это означает, что переменная 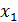исключена из всех уравнений, кроме первого.

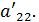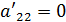Далее рассмотрим элемент Если , то перестановкой строк можно добиться, чтобы 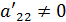. Разделим вторую строку на 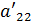, тогда новый элемент 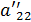=1. Обнуляем все элементы второго столбца, кроме первого и второго. Чтобы получить ноль во втором элементе третьей строки, умножаем третью строку на 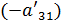и складываем со второй. Далее умножаем вторую строку на 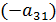и складываем с третьей и т.д. Получим нули во втором столбце во всех элементах, начиная с третьего. Для системы это означает, что переменная 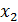исключена из всех уравнений, кроме первого и второго. Продолжая процедуру, после (r-1)-го шага получим матрицу

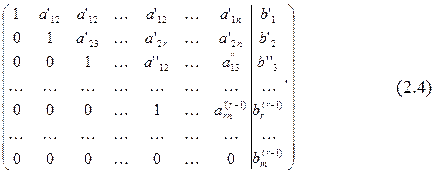
Для любой совместной системы числа 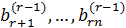должны быть равны нулю (если хотя бы одно из них отлично от нуля, то система несовместна). Отбрасывая нулевые строки, получаем матрицу ступенчатого вида. Выделим базисный минор r-ого порядка. Столбцы базисного минора будем называть базисными столбцами. Базисные столбцы определяют, какие переменные будут базисными. Если, например, базисными столбцами являются первый, четвертый и пятый столбцы матрицы, то и базисными переменными будут 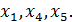Остальные переменные называются свободными и выражаются через базисные.

Переход системы (2.1) к равносильной ей системе (2.4) называется прямым ходом метода Гаусса. Далее аналогично тому, как обнуляли элементы под элементами 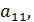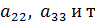. д., необходимо обнулить элементы над элементами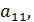 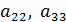и т. д. Но теперь надо начинать с последнего элемента 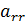и обнулить все элементы над ним. Затем перейти к (r-1) столбцу и обнулить все элементы над элементом 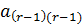и т. д., пока не дойдем до первого столбца. Такие преобразования называются обратным ходом метода Гаусса. Однако, описанная процедура верна только в случае, если базисный минор находится в левом верхнем углу матрицы системы (этого всегда можно добиться, если перенумеровать неизвестные, поэтому более общий случай не рассматривается).

Рассмотрим алгоритм применения метода Гаусса на простых примерах.

Пример 2.6. Решить систему линейных алгебраических уравнений методом Гаусса:

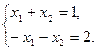
Решение. Преобразуем расширенную матрицу системы:

~ .

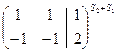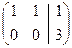Отсюда следует, что 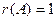, , 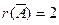т.е. исходная система несовместна. Заметим, что, применяя метод Гаусса (т.е. исключая неизвестные), мы одновременно проводим исследование системы на совместность (т.е. отыскиваем ранги матрицы системы и расширенной матрицы).

Пример 2.7. Решить систему линейных алгебраических уравнений методом Гаусса:

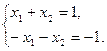
Решение. Исследуем систему на совместность:

~ ~ .

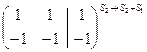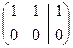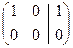Отсюда следует, что 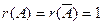– система совместна.

Поскольку ранг матрицы меньше числа неизвестных, то система имеет бесчисленное множество. Базисный минор |1| выделяется только из первого столбца, поэтому первая переменная x₁ - базисная, а вторая x₂ свободная. Обозначая x₂ =t, получаем общее решение системы: x₁₌ t, x₂ =t или в векторном виде 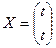, где t - произвольная постоянная.

Придавая t различные действительные значения, получаем бесконечное множество решений исходной системы.

Пример 2.8. Решить систему линейных алгебраических уравнений методом Гаусса:

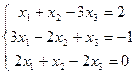
Решение.Выпишем расширенную матрицу данной системы

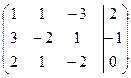
и произведем следующие элементарные преобразования над ее строками: из ее второй и третьей строк вычтем первую, умноженную соответственно на 3 и 2, затем третью строку умножим на (-5) и прибавим к ней вторую:

~ ~ ~ ~ .

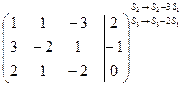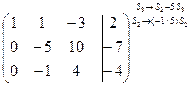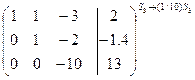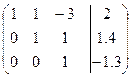Имеем 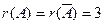– система совместна и имеет единственное решение (ранг совпадает с числом неизвестных). Поэтому все переменные будут базисными и переходим к обратному ходу метода Гаусса, т.е. обнуляем элементы над главной диагональю:

~ ~ .

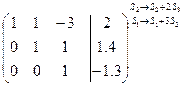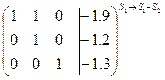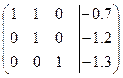В результате всех этих преобразований x₁=-0.7, x₂=-1.2, x₃=-1.3, или в векторном виде

.

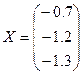Пример 2.9. . Исследовать систему уравнений и решить ее, если она совместна.

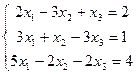
Решение.Исследуем данную систему на совместность. Выпишем расширенную матрицу системы

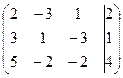
Преобразуем ее следующим образом: из третьей строки вычитаем первую и вторую строки, затем к первой строки прибавляем вторую, умноженную на 3:

~ ~ .

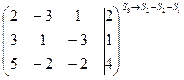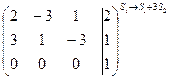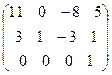Теперь ясно, что 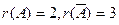. Согласно теореме Кронекера - Капелли, из того, что 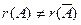, следует несовместность исходной системы.

Пример 2.10. Исследовать систему уравнений и решить ее, если она совместна.

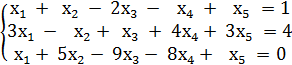
Решение.Будем находить ранги матриц A и 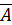методом элементарных преобразований, приводя одновременно систему к ступенчатому виду:

~ ~ .

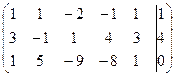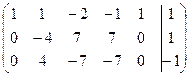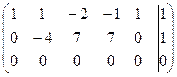Очевидно, что r(A) = r 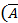)=2. Так как ранг матрицы меньше числа неизвестных, то система имеет бесконечное множество решений. В качестве базисного минора можно взять М = 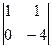=-4 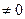, который содержит 1-ый и 2-ой столбцы матрицы. Поэтому переменные x₁ и x₂ возьмем в качестве базисных, а переменные x₃, x₄, x₅ будет свободными. Разделим вторую строку на (-4), а нулевые строки вычеркнем. Далее, используя процедуру обратного хода метода Гаусса, обнуляем верхнюю часть матрицы (т. е элемент а₁₂ ), умножив вторую строку на 3 и сложив ее со второй строкой

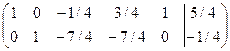
Полагая x₃=t, x₄=u, x₅=v (где t, u, v – произвольные постоянные), получим

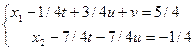
Отсюда 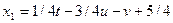, 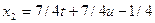. Таким образом, общее решение системы имеет вид

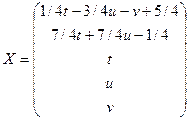, где t, u, v – произвольные постоянные.

Придавая свободным переменным конкретные числовые значения, будем получать частные решения. Например, при t= u= v = 0 x₁= 5/4, x₂ = - 1/4. Вектор (5/4, - 1/4, 0, 0, 0) является частным решением данной системы.

Пример 2.11. Исследовать систему уравнений и найти общее решение в зависимости от значения параметра а.

2x₁ - x₂ + x₃ + x₄ = 1,

x₁ + 2x₂ - x₃ + 4x₄ = 2,

x₁ + 7x₂ - 4x₃ + 11x₄ = a.

Решение.Данной системе соответствует матрица 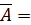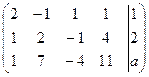. Имеем ~ ~ .

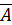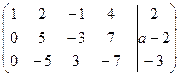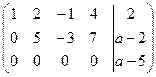Система совместна, если r(A) = r( 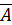) = 2, т.е. только в случае, если a=5. Так как ранг матрицы меньше числа неизвестных, то система имеет бесконечное множество решений. В качестве базисного минора можно взять М = 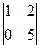=5 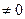, который содержит 1-ый и 2-ой столбцы матрицы. Поэтому переменные x₁ и x₂ возьмем в качестве базисных, а переменные x₃, x₄ будут свободными. Разделим вторую строку на 5, а нулевую строку вычеркнем. Получим

.

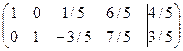Общее решение в этом случае имеет вид:

x₂ = 3/5 + 3/5x₃ - 7/5x₄, x₁ = 4/5 - 1/5x₃ - 6/5x_4.