Канонический вид квадратичной формы.
Определение. Однородный многочлен второй степени относительно переменных 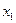 и
и 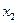
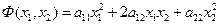
не содержащий свободного члена и неизвестных в первой степени называется квадратичной формой переменных 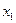 и
и 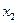 .
.
Определение. Однородный многочлен второй степени относительно переменных 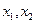 и
и 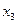
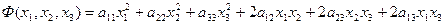 ,
,
не содержащий свободного члена и неизвестных в первой степени называется квадратичной формой переменных 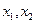 и
и 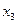 .
.
Рассмотрим квадратичную форму двух переменных. Квадратичная форма имеет симметрическую матрицу 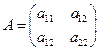 . Определитель этой матрицы называется определителем квадратичной формы.
. Определитель этой матрицы называется определителем квадратичной формы.
Пусть на плоскости задан ортогональный базис 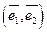 . Каждая точка плоскости имеет в этом базисе координаты
. Каждая точка плоскости имеет в этом базисе координаты 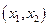 .
.
Если задана квадратичная форма 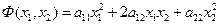 , то ее можно рассматривать как функцию от переменных
, то ее можно рассматривать как функцию от переменных 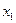 и
и 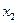 .
.
2. Приведение квадратичных форм к каноническому виду
Рассмотрим некоторое линейное преобразование А с матрицей 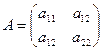 . Это симметрическое преобразование можно записать в виде:
. Это симметрическое преобразование можно записать в виде:
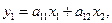
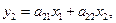
где 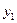 и
и 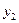 координаты вектора
координаты вектора 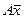 в базисе
в базисе 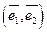 . Очевидно, что квадратичная форма может быть записана в виде
. Очевидно, что квадратичная форма может быть записана в виде
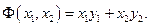
Геометрический смысл числового значения квадратичной формы Ф в точке с координатами 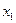 и
и 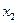 суть скалярное произведение
суть скалярное произведение 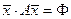 .
.
Если взять другой ортонормированный базис на плоскости, то в нем квадратичная форма Ф будет выглядеть иначе, хотя ее числовое значение в каждой геометрической точке не изменится. Если найти такой базис, в котором квадратичная форма не будет содержать координат в первой степени, а только координаты в квадрате, то квадратичную форму можно будет привести к каноническому виду.
Если в качестве базиса взять совокупность собственных векторов линейного преобразования, то в этом базисе матрица линейного преобразования имеет вид:
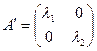 .
.
При переходе к новому базису от переменных 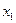 и
и 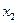 перейти к переменным
перейти к переменным 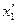 и
и 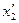 . Тогда:
. Тогда:
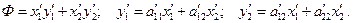
Следовательно,  .
.
Выражение 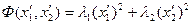 называется каноническим видом квадратичной формы. Аналогично можно привести к каноническому виду квадратичную форму с большим числом переменных.
называется каноническим видом квадратичной формы. Аналогично можно привести к каноническому виду квадратичную форму с большим числом переменных.
Теорема. (Лагранжа).Любую квадратичную форму с помощью невырожденного линейного преобразования неизвестных можно привести к каноническому виду.
С помощью невырожденного линейного преобразования приведем квадратичную форму 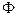 к виду, в котором
к виду, в котором 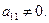 Все слагаемые, содержащие
Все слагаемые, содержащие 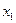 , соберем в одну скобку и дополним эту скобку до полного квадрата, получим
, соберем в одну скобку и дополним эту скобку до полного квадрата, получим
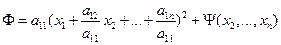 ,
,
где оставшиеся слагаемые образуют квадратичную форму 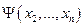 от неизвестных
от неизвестных 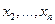 . Невырожденное линейное преобразование неизвестных
. Невырожденное линейное преобразование неизвестных
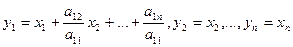
приводит квадратичную форму к виду
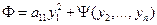 .
.
Повторив рассуждения, с учетом того, что последовательное выполнение невырожденных линейных преобразований вновь невырожденное линейное преобразование, получим утверждение теоремы.
Пример. Приведите с помощью невырожденного линейного преобразования неизвестных к каноническому виду квадратичную форму 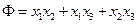 .
.
Линейное преобразование 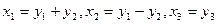 приводит квадратичную форму к виду
приводит квадратичную форму к виду 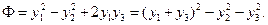 А линейное преобразование
А линейное преобразование 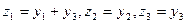 - к виду
- к виду 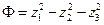 . Найдем сквозное линейное преобразование
. Найдем сквозное линейное преобразование 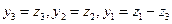
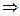
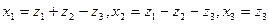 . Так как определитель матрицы линейного преобразования
. Так как определитель матрицы линейного преобразования
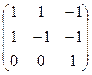
равен – 2, то оно является невырожденным.
Ответ: невырожденное линейное преобразование неизвестных 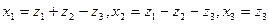 приводит форму к каноническому виду
приводит форму к каноническому виду 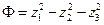 .
.
Квадратичная форма с действительными коэффициентами имеет нормальный вид, если в ее записи нет слагаемых с произведениями неизвестных, а квадраты переменных входят с коэффициентами 1 или -1 или совсем не входят. После изменения нумерации переменных нормальный вид можно переписать в виде: сначала идут коэффициенты 1, затем -1, а затем нули,
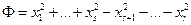 .
.
Дата добавления: 2015-09-29; просмотров: 849;
