ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТов ТРЕНИЯ СКОЛЬЖЕНИЯ И ТРЕНИЯ КАЧЕНИЯ С ПОМОЩЬЮ НАКЛОННОГО маятникА

Внешнее трение твердых тел – это механическое сопротивление, возникающее в плоскости касания двух прижатых друг к другу тел при их относительном перемещении. Сила сопротивления, направленная противоположно относительному перемещению данного тела, называется силой трения. Внешнее трение является диссипативным процессом, сопровождающимся выделением теплоты, электризацией тел, их разрушением и т.д.

В зависимости от вида перемещения одного тела по другому различают трение скольжения и трение качения. Каждый из этих видов внешнего трения характеризуется соответствующим коэффициентом.

Коэффициентом трения скольжения k называется величина, определяемая отношением силы трения к силе реакции опоры, направленной по нормали к поверхности касания.

Коэффициентом трения качения k₁ называется величина, определяемая отношением тормозящего момента силы трения качения к силе нормальной реакции.

В настоящей работе экспериментально определяются коэффициенты трения скольжения и трения качения стального шарика по стальной пластине с помощью наклонного маятника (рис. 3.1).

Сначала рассмотрим трение скольжения шарика по наклонной плоскости. Если маятник отклонить вдоль наклонной плоскости на некоторый угол и отпустить, то начнутся колебания, которые будут затухать под действием силы трения маятника о плоскость, сопротивления среды и трения в подвесе маятника. Основной причиной в данном случае будет интересующее нас трение скольжения. Двумя другими силами трения можно пренебречь.

Пусть масса маятника m. Основные силы, действующие на маятник в отклоненном положении, изображены на рис. 3.1. Их четыре: сила тяжести 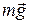, сила 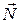нормальной реакции плоскости, сила 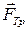трения скольжения и сила 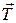натяжения подвеса. Сила трения по определению связана с силой реакции плоскости формулой

F_Тр = k N , (3.1)

где k – коэффициент трения скольжения.

Разложим силу тяжести на компоненты 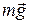_ïï, параллельную плоскости, и 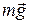_^, перпендикулярную плоскости. Сила 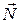нормальной реакции уравновешивает компоненту 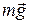_^, следовательно, эти два вектора равны по величине: = =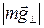mg×sin g и для силы трения получается выражение

F_Тр = k mg×sin g .

Обозначим начальный угол отклонения маятника вдоль плоскости a₀, максимальный угол в противоположную сторону (через половину периода) a_1/2, угол отклонения через период – a₁. При медленном убывании амплитуды потери энергии за каждый период приблизительно одинаковы и a_1/2=(a₀+a₁)/2. За период точка касания маятника проходит путь S=l×(a₀+2a_1/2+a₁)=2l×(a₀+a₁), где l – длина маятника.

При этом сила трения совершает работу

А_Тр = – F_Тр S = – 2 k m g l sin g (a₀ + a₁) . (3.2)

На величину этой работы уменьшается полная механическая энергия маятника. В крайних положениях эта энергия состоит только из потенциального вклада mgh, поэтому

А_Тр = m g h₀ – m g h₁ , (3.3)

где h₀, h₁ – высоты подъема маятника в крайнем положении, соответствующие углам a₀, a₁.

С помощью рис. 3.2 найдем, как высота подъема h связана с углом a отклонения маятника. В отклоненном положении центр тяжести маятника поднят вдоль плоскости на отрезок BD=AC=l (l–cos a). Из треугольника BDE получаем:

h = BD cos g = l cos g (1 – cos a) =
= 2l cos g sin²(a/2) » l cos g×a²/2 .

Последнее приближенное равенство справедливо при малых углах, в этом случае sin (a/2)»a/2. Подставляя выражение для каждой из высот в уравнение (3.3) и учитывая формулу (3.2), получим

.

Сократив с обеих сторон равенства одинаковые множители, получим следующее выражение:

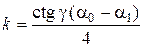. (3.4)

Рассмотрим n последовательных колебаний наклонного маятника. Формула, аналогичная (3.4), будет справедлива для каждого из n периодов:

(3.5)

Здесь a₂, a₃, …, a_n – угловые амплитуды отклонения после второго, третьего, …, n-го периода колебаний. Сложим все формулы (3.5). В правой части все промежуточные углы a₂, a₃, …, a_n–1 сократятся. После деления на число периодов n получим окончательную формулу для определения коэффициента трения скольжения:

. (3.6)

В том случае, когда маятник представляет собой шарик, катящийся без проскальзывания по наклонной платформе, основной диссипативной силой служит сила F_тр.к. трения качения. Тормозящий момент силы трения качения пропорционален силе нормальной реакции, то есть

F_тр.к. R = k₁ N , (3.7)

где k₁ – коэффициент трения качения; R – радиус кривизны катящегося тела. Рассуждения, приведенные выше для трения скольжения, можно повторить для трения качения, используя вместо формулы (3.1) соотношение (3.7). При этом для коэффициента трения качения получим

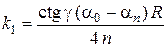. (3.8)

Таким образом, лабораторная работа заключается в экспериментальной проверке формулы (3.6) для определения коэффициента трения скольжения k и формулы (3.8) для коэффициента трения качения k₁.