Минимизация логических функций методом Квайна

С использованием метода Квайна функция представ­ляется в минимальной дизъюктивной либо конъюктив- ной форме (МДНФ либо МКНФ). Минимизируется число членов и число переменных в каждом члене.

Выполняется в следующей последовательности:

1) функция, представленная в канонической форме СДНФ (либо СКНФ), приводится к сокращенной форме;

2) от сокращенной формы переходят к минимальной.

Переход от СДНФ к сокращенной форме основан на

последовательном применении двух операций: склеивания и поглощения. Для выполнения операции склеивания в выражении функции выявляют пары членов вида

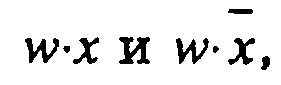
различающиеся лишь тем, что один из аргументов в одном из членов представлен без инверсии, а в другом — с инвер­сией. Затем проводится склеивание таких пар членов (1.8):

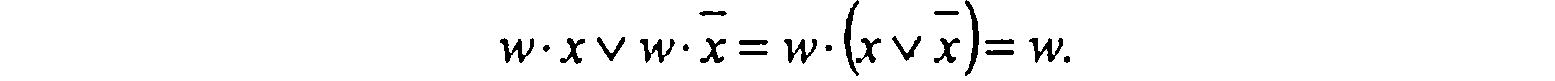
Операция поглощения основана на равенстве:

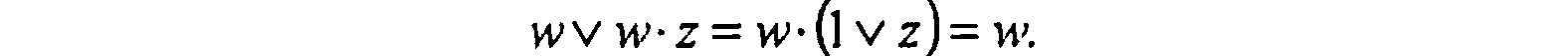
Член w поглощает член w-z. Операции склеивания и поглощения выполняются последовательно до тех пор, пока это возможно. В полученной сокращенной форме в каж­дом члене нельзя уменьшить число аргументов (входных переменных).

Проведем минимизацию методом Квайна для СДНФ.

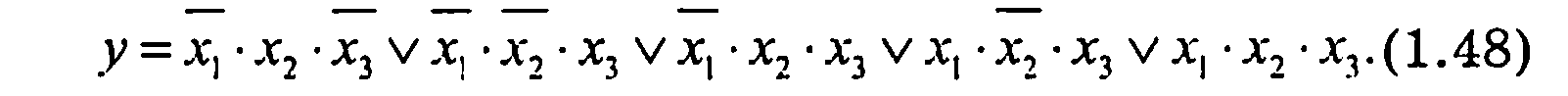
Сравнивая каждый из членов с другим, находим склеивающиеся пары:

(1-й и 3-й члены):

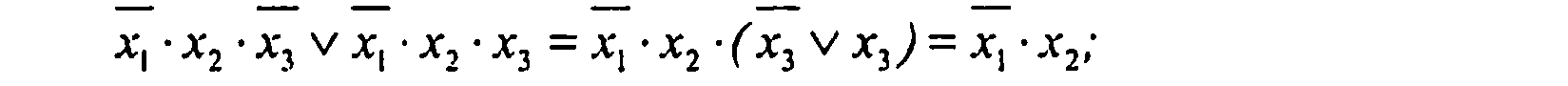
(2-й и 3-й члены):

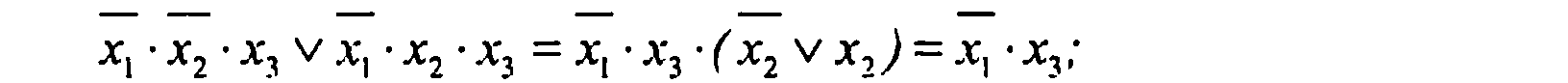
(2-й и 4-й члены):

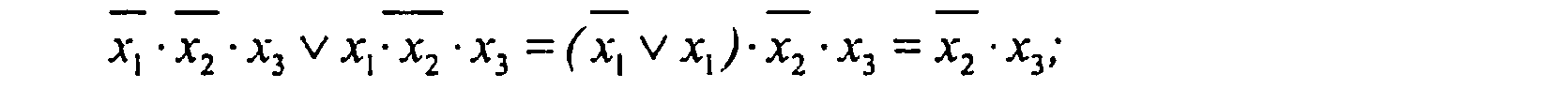
(3-й и 5-й члены):

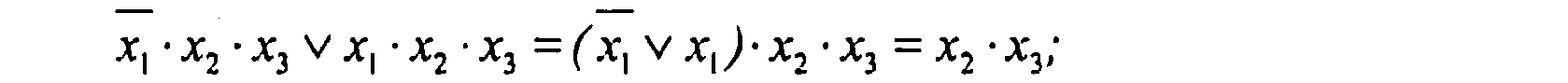
(4-й и 5-й члены):

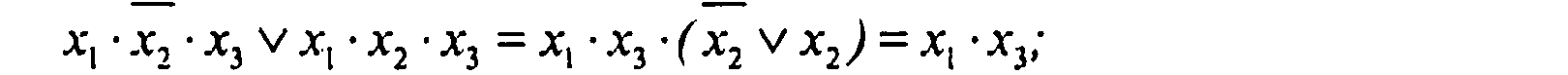
В выражении остаются члены, для которых повторя­ем операции склеивания и поглощения:

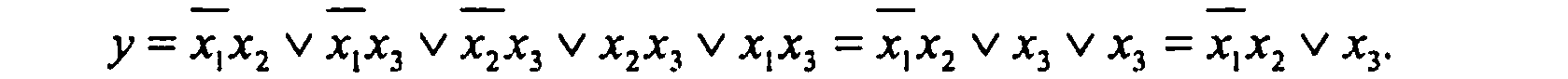
Склеивались (2-5) и (3-4) члены. В данном примере дальнейшее выполнение операций склеивания и поглоще­ния невозможно. Полученная сокращенная форма являет­ся минимальной.

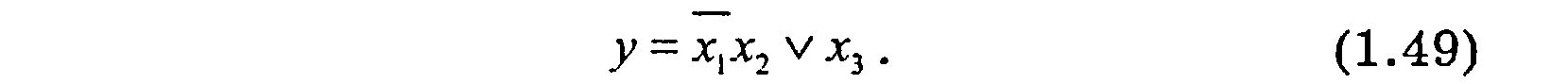
Выражение (1.49) значительно проще выражения (1.48). Для построения структурной схемы достаточно трех элементов (рис. 1.12).

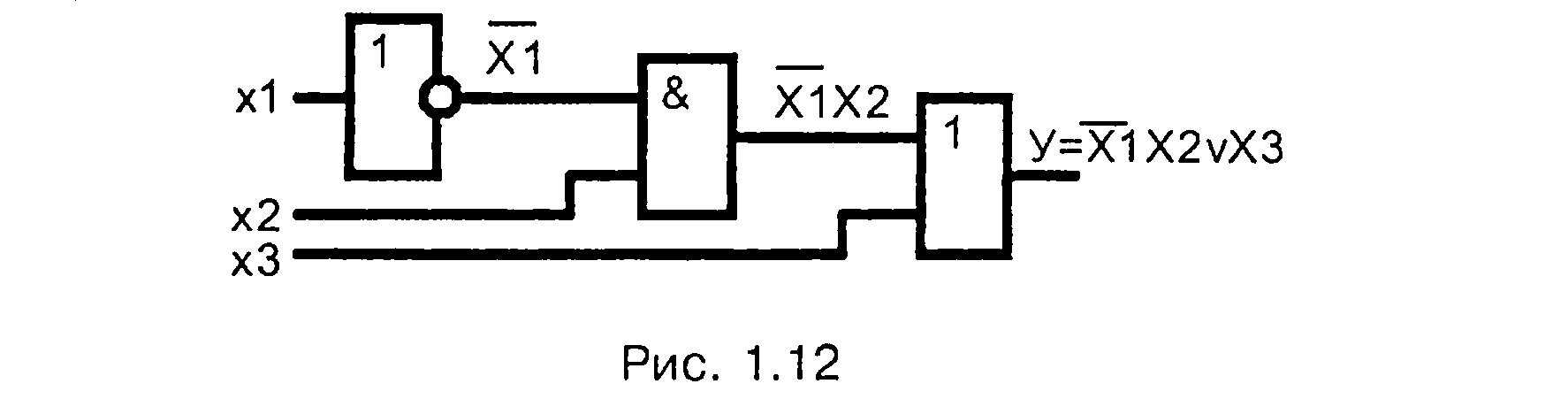
Члены сокращенной формы (1. 49) являются просты­ми импликантами.

Сокращенная форма после проведения операций скле­ивания и поглощения хотя и содержит только простые импликанты, но может иметь «лишние» члены, которые можно исключить, не изменяя значение функции. Пере­ход от сокращенной формы к минимальной осуществля­ется с помощью импликантных таблиц.

Рассмотрим пример. Функция, выраженная СДНФ,

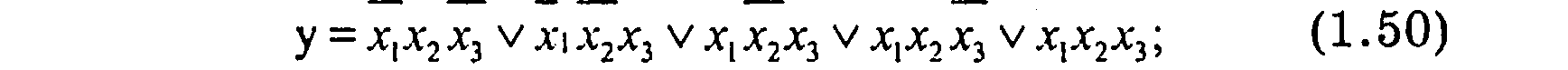
после операций склеивания и поглощения принимает со­кращенную форму

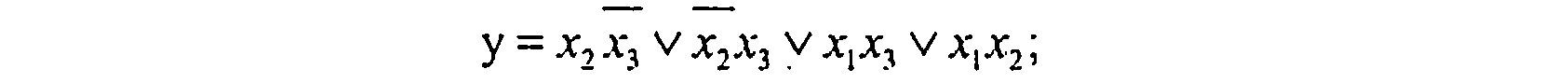
которая не является минимальной.

Для определения и исключения «лишних» импликант строят импликантную таблицу (таблица 1.12). Каждая строка импликантой таблицы является простой импликантой, столбцами — члены исходной СДНФ.

В импликантной таблице ставятся отметки. Если про­стая импликанта является составной частью какой-либо конституенты единицы, то на пересечении строки и столбца ставится условный знак. Так третья импликанта (x₁,x₃) по­глощает третью 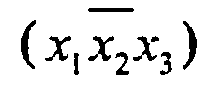и пятую (x₁,x₂,x₃) конституенты еди­ницы. Если имеется столбец, перекрываемый только одной простой импликантой, то данная импликанта составляет ядро и не может быть исключена. В таблице 1.12 в ядро входят первая и вторая импликанты. Третья (x₁,x₃) и четвертая (х₁,x₂) импликанты являются лишними. Но одно­временно обе они исключены быть не могут, так как в этом случае без отметки останется пятый столбец (х₁,x₂,x₃).

Таким образом, для выражения (1.50) возможны две тупиковые формы:

Обе тупиковые формы имеют одинаковое количество членов, и любая из них может быть выбрана в качестве минимальной ДНФ (МДНФ).

Минимизацию функции методом Квайна можно прово­дить с использованием совершенной конъюктивной нор­мальной формы (СКНФ). – Самостоятельно, будет КР

Метод Квайна при переходе от сокращенной формы к минимальной в некоторых случаях приводит к неодноз­начному выбору, что не совсем удобно для автоматизиро­ванного проектирования.