РАЗВИТИЕ ГОРЕНИЯ 3 страница
Корольченко А.Я. Процессы горения и взрыва
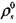 = 0,89 • 103 кг/м3, uH м"» = 5 • 10-2 м/сек, uH макс = 0,5 м/сек.
= 0,89 • 103 кг/м3, uH м"» = 5 • 10-2 м/сек, uH макс = 0,5 м/сек.
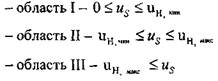
|
|
Проанализируем ситуацию, когда пламя распространяется по азровзве-си сверху вниз. Анализ устойчивости решения соотношения (4.37) приводит к выделению трех областей качественно различного поведения пламени:
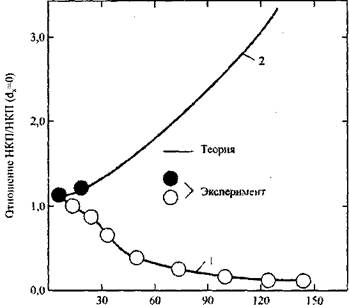
Рис. 4.22. Экспериментальная и расчетная зависимости НКП (в относительных единицах) от концентрации тетралина в воздухе
1 - движение пламени снизу вверх
2 - движение пламени сверху вниз
Распространение пламени при скоростях оседания частиц, приходящихся на область I, незначительно отличается от случая парофазного горения. График скорости распространения пламени незначительно сдвинут относительно опорного (кривая 2 на рис. 4.21), сохраняя все его особенности, включая близкие значения нижнего концентрационного предела
ПО
Глава 4. Развитие горения
распространения пламени. Для аэрозолей органических веществ область соответствия ограничена величиной us <<5 • 10-2 м/сек, что с учетом соотношения (4.27) приводит к ограничению диаметра частиц ds 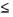 10мкм.
10мкм.
Область II характеризуется появлением решения, отвечающего неустойчивому движению фронта пламени (кривая 3 на рис. 4.21, неустойчивая ветвь обозначена пунктиром). При этом нижний концентрационный предел распространения пламени и предельная скорость распространения пламени резко возрастают с увеличением диаметра частиц (соответственно с увеличением скорости оседания).
Полагая линейную зависимость ин от концентрации горючего в околопредельной смеси (что справедливо для скоростей распространения пламени us .uf <иН,макс .0,5 ), получим выражения для НКП 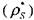 и пре-
и пре-
дельной скорости 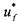 следующего вида:
следующего вида:
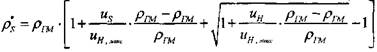
|
(4.38)
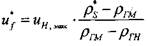
|
(4.39)
Результаты вычисления нижнего концентрационного предела распространения пламени по соотношению (4.38) сопоставлены с экспериментальными данными на рис. 4.22. При скорости оседания частиц us > ин,макс
(область III) распространение пламени вниз оказывается невозможно, поскольку частицы горючего движутся быстрее фронта пламени и горючее не поступает в зону горения. Оценка диаметра частиц, при котором реализуется рассмотренный случай, для тетралина дает ds> 140 мкм.
В заключение данного раздела сформулируем выводы для случая относительного движения фаз в горящей аэровзвеси. Относительное движение фаз аэровзвеси влияет на температуру горения и, следовательно, на скорость распространения пламени. Если относительная скорость частиц и воздуха (us-u1) направлена в сторону фронта пламени, горение аэровзвеси ускоряется по отношению к случаю неподвижных фаз: возрастают температура горения и скорость распространения пламени. Если (us -u1) направлена от фронта пламени, горение может замедляться вплоть до полного прекращения.
Корольченко А.Я. Процессы горения и взрыва______________________
Гидродинамический анализ горения аэрозолей.Сильное влияние относительного движения фаз аэрозоля на распространение пламени наталкивает на поиски причин, вызывающих это относительное движение в горящих аэродисперсных системах. Априори можно предположить, что столь сильное влияние должно обусловливать обратную связь процессов в горящем аэрозоле, которая способна интенсифицировать это движение (рассеяние) фаз аэрозоля. В этом отношении представляет большой интерес гидродинамический анализ поведения фаз аэрозоля в условиях возмущения плоского фронта пламени. Как будет показано, гидродинамика горения двухфазной системы такова, что процессы разрушения ламинарного фронта пламени в таких системах интенсифицируются в большей степени, чем в гомогенных средах. Излагаемый ниже механизм разрушения плоского фронта пламени в аэродисперсных системах, по-видимому, обусловливает переход от плоско-ламинарных режимов горения аэрозолей к турбулентному.
Для этого исследуется линейная устойчивость плоского фронта пламени, рассматриваемого как поверхность гидродинамического разрыва. Возможность получить точное решение задачи в линейном приближении даст в дальнейшем возможность исследования характера гидродинамического движения фаз горящего аэрозоля при значительных искривлениях зоны горения.
Устойчивость плоской зоны горения в аэрозоле будем исследовать по следующей схеме. Постулируя кондуктивный механизм распространения пламени, характерные размеры в задаче выберем таким образом, чтобы шириной зоны значительных градиентов физических параметров (область прогрева свежей смеси, область химической реакции и область релаксации мелкомасштабных - на длинах порядка расстояний между частицами - неоднородностей распределения физических величин) можно было пренебречь. В дальнейшем эту зону будем рассматривать в виде поверхности газодинамического разрыва и именовать фронтом пламени. Предположим, что в невозмущенном горением аэрозоле горючее (монодисперсные частицы) распределено равномерно по объему и находится с окислителем (воздухом) в относительном покое, т. е. действием силы тяжести пренебрегаем. Для исследования устойчивости плоского фронта пламени выберем систему координат, в которой первоначально невозмущенное пламя покоится и совпадает с плоскостью координат (y,z), свежая
Глава 4. Развитие горения
смесь (х < 0) набегает на фронт пламени со скоростью u1 = us, газообразные продукты горения (х > 0) уносятся со скоростью и2. Штрихом отмечены малые нестационарные добавки - возмущения величин, характеризующих стационарное поле течения; 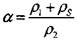 коэффициент расширения продуктов горения; ин - нормальная скорость распространения пламени по аэрозолю, которая принимается равной нормальной составляющей скорости поступления воздуха свежей смеси во фронт пламени (в невозмущенном состоянии ин =u = us = u2/a); рз° - плотность материала
коэффициент расширения продуктов горения; ин - нормальная скорость распространения пламени по аэрозолю, которая принимается равной нормальной составляющей скорости поступления воздуха свежей смеси во фронт пламени (в невозмущенном состоянии ин =u = us = u2/a); рз° - плотность материала
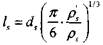
|
частиц; ds - диаметр частиц;
частицами в аэрозоле; 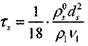 - стоксово время релаксации относи-
- стоксово время релаксации относи-
тельной скорости фаз аэрозоля; К6 - константа диффузионного горения частицы топлива; tf - характерное время релаксации процессов во фронте пламени; lf = а ин tf - физическая толщина фронта пламени;
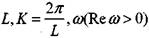 - соответственно период, волновой вектор и инкремент роста во времени возмущения фронта пламени. В дальнейшем для количественных оценок будут использоваться следующие значения параметров, характеризующих нижнепредельный аэрозоль тетралина:
- соответственно период, волновой вектор и инкремент роста во времени возмущения фронта пламени. В дальнейшем для количественных оценок будут использоваться следующие значения параметров, характеризующих нижнепредельный аэрозоль тетралина:
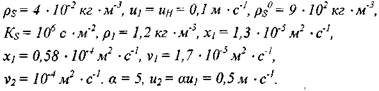
Предположим, что характерное время релаксации процессов во фронте
среднее расстояние между
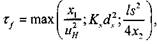
|
| где члены в круглых |
пламени определяется как
скобках соответствуют стадии кондуктивного прогрева свежей смеси, времени диффузионного горения частицы, а также времени релаксации (в диффузионном приближении) мелкомасштабных неоднородностей горячей аэродисперсной системы. Оценки показывают, что в практически важном случае горения частиц аэрозоля в диффузионном режиме (ds 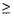 10-4 м):
10-4 м):
Аэрозоль с концентрацией горючего, равной нижнему концентрационному пределу распространения пламени.
Корольченко А.Я. Процессы горения и взрыва
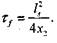
|
Рассмотрим малое, периодическое вдоль оси у (с периодом L) возмущение поверхности фронта пламени, вызывающее возмущение векторов скорости фаз в плоскости (х, у). Исследование устойчивости фронта пламени к выбранному типу возмущений будем проводить в приближении:
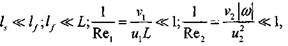
|
(4.40)
где Re - число Рейнольдса, построенное по характерному масштабу не-однородностей, вносимых возмущением, и равному соответственно L и 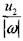
Первое из условий (4.40) оправдывает принятое изображение фаз в виде взаимопроникающих континиумов, второе условие отвечает описанию фронта пламени поверхностью газодинамического разрыва, остальные условия определяют асимптотическое приближение, когда эффектами переноса (вязкостью и теплопроводностью газа) в уравнениях движения среды можно пренебречь. Течение продуктов горения и свежей смеси, возникающее в результате возмущения вблизи фронта пламени, подчиняется линеаризованным уравнениям механики соответственно одно- и двухскоро-стного континиума с точки зрения феноменологического подхода:
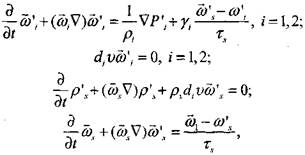
|
(4.41)
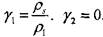
|
где
Отметим, что вблизи нижнего концентрационного предела распространения пламени 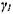 «: 1 (для тетралина
«: 1 (для тетралина 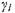 = 0,032), т. е. массовая доля конденсированной фазы в аэрозоле мала. Далее легко получить решение (4.41) для возмущений, пропорциональных примерно exp (wt + iKy). Ана-
= 0,032), т. е. массовая доля конденсированной фазы в аэрозоле мала. Далее легко получить решение (4.41) для возмущений, пропорциональных примерно exp (wt + iKy). Ана-
Глава 4. Развитие горения
лиз показывает, что решение не имеет особенностей при 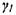 = 0, и в силу малости параметра
= 0, и в силу малости параметра 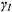 влиянием конденсированной фазы аэрозоля как на движение воздуха, так и в уравнениях баланса (граничные условия) будем в дальнейшем пренебрегать, т. е. у/ —* 0. Тогда решение для возмущенных параметров газовой фазы принимает вид:
влиянием конденсированной фазы аэрозоля как на движение воздуха, так и в уравнениях баланса (граничные условия) будем в дальнейшем пренебрегать, т. е. у/ —* 0. Тогда решение для возмущенных параметров газовой фазы принимает вид:
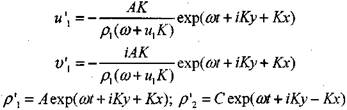
(4.42)
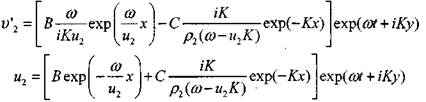
|
где А, В, С- произвольные константы
Решение для возмущенных параметров конденсированной фазы имеет вид
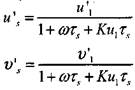
|
(4.43)
В соответствии с выбранным типом возмущений форма поверхности фронта пламени представляется в виде:
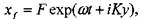
(4.44)
где F — произвольная константа.
На рис. 4.23 приведена схема «линий тока» конденсированной (пунктирные линии) и газовой (сплошные линии) фаз вблизи искривленного фронта пламени. Искривление и ускоренное движение фронта вызывает изменение направления и величины скорости движения воздуха. В свою очередь, воздух увлекает частицы горючего, которые в силу инерционности отстают от ускоренно движущейся газовой фазы. Последнее при-
Корольченко А.Я. Процессы горения и взрыва
водит к различию в скоростях поступления горючего и окислителя во фронт пламени (фазодинамический эффект), что с необходимостью ведет к изменению температуры горения и нормальной скорости горения аэрозоля, влияющим на дальнейшее ускорение и искривление фронта. Отмеченная связь процессов в горящем аэрозоле определяет возможность существования специфического для дисперсных систем механизма разрушения плоского фронта пламени наряду с его гидродинамической неустойчивостью, известной из теории гомогенного горения. Установим количественную связь между инкрементами роста и волновыми векторами периодических возмущений плоского фронта пламени.
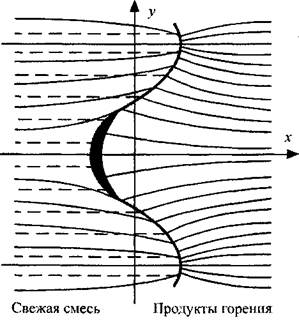
Рис. 4.23 Поле течения фаз вблизи искривленного фронта пламени
В решения (4.42), (4.43) и уравнение искривленной поверхности фронта (4.44) входят четыре неопределенные константы А, В, С, F, которые можно найти из граничных условий: двух условий неразрывности движения фронта пламени относительно свежей смеси и продуктов горения и двух условий сохранения компонент импульса произвольного элемента фронта пламени. Ввиду указанного влияния возмущений фронта пламени на нормальную скорость горения (UH = 0), граничные условия на
Глава 4. Развитие горения
фронте пламени следует модифицировать с учетом влияния коротковолновых возмущений на нормальную скорость распространения пламени
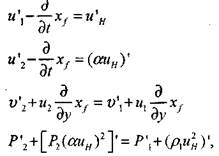
|
(4.45)
где приращение (штрих) берется по правилу взятия производной.
Для использования граничных условий (4.45) необходимо определить вид зависимости флуктуации 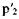 и
и 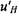 от порождающих их флуктуации параметров свежей смеси
от порождающих их флуктуации параметров свежей смеси 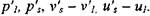 Из соотношений
Из соотношений
(4.42), (4.43) следует 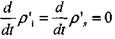 , следовательно,т.
, следовательно,т. 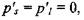 е. в
е. в
линейном приближении концентрация фаз аэрозоля не изменяется. Из симметрии плоского фронта пламени к отражению в плоскости (х, z) следует, что искомая зависимость не чувствительна к изменению знака аргумента 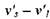 , т. е. в линейном приближении отсутствует. Таким образом, флуктуации
, т. е. в линейном приближении отсутствует. Таким образом, флуктуации 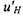 и
и 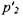 пропорциональны
пропорциональны 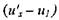
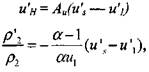
|
(4.46) (4.47)
где А„ - коэффициент, определяемый конкретными особенностями механизма распространения пламени по аэрозолю.
Выражение для коэффициента пропорциональности в (4.47) получено в предположении о сходстве теплофизических свойств воздуха и продуктов горения, причем принимали, что плотность последних обратно пропорциональна температуре горения, линейно зависит от относительного содержания горючего в потоке свежей смеси во фронт пламени. Отметим, что соотношения (4.46) и (4.47) отражают основные проявления фазодинамического эффекта при возмущении плоского стационарного фронта пламени - соответственно изменение нормальной скорости горения и изменение плотности продуктов горения (температуры го-
Корольченко А.Я. Процессы горения и взрыва______________________
рения). Из (4.47) с учетом (4.42), (4.43) следует, что периодическое возмущение фронта пламени приводит к уменьшению плотности (увеличению температуры) продуктов горения для выпуклых (по отношению к продуктам реакции) участков фронта пламени и увеличение плотности (уменьшение температуры) продуктов горения для вогнутых участков.
Подставляя решения (4.42) и (4.43) в условия (4.45) с учетом (4.46),
(4.47) и соотношений 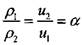 , вытекающих из постановки задачи
, вытекающих из постановки задачи
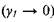 ', получим систему из четырех однородных алгебраических уравнений относительно неопределенных коэффициентов А, В, С, F. Для того, чтобы существовало нетривиальное решение этой системы, необходимо приравнять нулю ее определитель. Это приведет к следующему уравнению для определения инкремента возмущений:
', получим систему из четырех однородных алгебраических уравнений относительно неопределенных коэффициентов А, В, С, F. Для того, чтобы существовало нетривиальное решение этой системы, необходимо приравнять нулю ее определитель. Это приведет к следующему уравнению для определения инкремента возмущений:
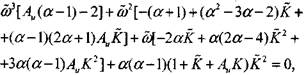 (4.48)
(4.48)
где введены безразмерные величины
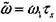 и
и 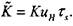
Уравнение (4.48) отличается от уравнения для инкрементов возмущений фронта пламени в гомогенных системах. Это связано с проявлением фазодинамического эффекта в аэродисперсных системах, т. е. отличием от нуля правых частей соотношений (4.46) и (4.47). Если в предельном переходе 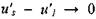 , что в соответствии с (4.43) означает
, что в соответствии с (4.43) означает 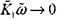 , оставить в уравнении (4.48) главные по порядку слагаемые, то с точностью до обозначений получим характеристическое уравнение:
, оставить в уравнении (4.48) главные по порядку слагаемые, то с точностью до обозначений получим характеристическое уравнение:
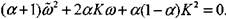 (4.49)
(4.49)
Условие 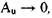 при котором обращается в нуль правая часть (4.46)
при котором обращается в нуль правая часть (4.46)
и исчезает влияние возмущения фронта пламени на нормальную скорость горения, недостаточно для предельного перехода уравнения (4.48) в уравнение (4.49). Это связано с дестабилизирующим воздействием на движение пламени в аэрозолях флуктуации коэффициента расширения продуктов горения, возникающих при искривлении фронта пламени.
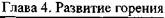
|
Из уравнения (4.48) следует, что необходимым условием развития возмущений фронта пламени в аэрозоле является различие плотностей продуктов горения и свежей смеси 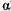 > 1.
> 1.
Необходимо отметить, что представление фронта пламени в виде поверхности газодинамического разрыва накладывает ограничение на величину инкрементов возмущений. Действительно, флуктуации нормальной скорости должны приводить к флуктуациям толщины фронта пламени, определяемой выражением 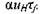 В рассматриваемом прибли-
В рассматриваемом прибли-
жении скорость изменения толщины фронта пламени должна быть намного меньше скорости роста амплитуды возмущений
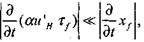
|
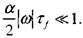
|
откуда с учетом (4.43-4.46) получим оценку
(4.50)
|
|
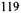
|
Корольченко А.Я, Процессы горения и взрыва
Для достаточно крупных частиц тетралина (ds >10-4 м) система условий (4.40) и (4.50) сводится к 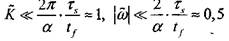 (4.51)
(4.51)
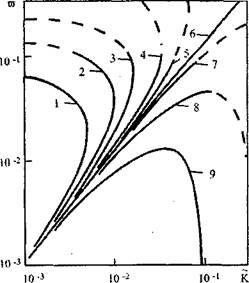
Семейство действительных решений (4.48), отвечающих различным значениям Аи, и решение (4.49) для 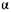 = 5 приведены на рис. 4.24 [нисходящая ветвь действительной составляющей комплексно-сопряженных корней (4.48), берущая начало в точке обращения в нуль производной
= 5 приведены на рис. 4.24 [нисходящая ветвь действительной составляющей комплексно-сопряженных корней (4.48), берущая начало в точке обращения в нуль производной
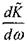 , на рисунке не показана]. Пунктиром обозначены ветви реше-
, на рисунке не показана]. Пунктиром обозначены ветви реше-
ний(4.48), анализ которых некорректен в силу приближения (4.51): выполнение необходимых неравенств наблюдается при различии сравниваемых величин не менее чем в 5 раз. При тепловом механизме распространения нижепредельного пламени наиболее вероятными, по-видимому, являются положительные значения коэффициента Аu которым отвечает увеличение (уменьшение) нормальной скорости горения для выпуклых (вогнутых) участков фронта пламени, коррелирующее с флуктуа-циями температуры горения. Вместе с тем возможны отрицательные значения параметра. При жесткой координатной связи передней границы пламени с решеткой частиц движение (дрейф) последних увлекает за собой пламя и в соответствии с (4.46) коэффициент Аu=-\. Из графиков (см. рис. 4.22) видно, что при Аи > 0 фазодинамический эффект дестабилизирует горение аэродисперсной системы по отношению к соответствующей гомогенной (кривая б), при Аи < 0 - стабилизирует. Существенная дестабилизация фронта пламени наступает в случае 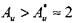 когда появляется многозначная зависимость инкрементов возмущения от волнового числа (кривые 1-3) и берущая начало при
когда появляется многозначная зависимость инкрементов возмущения от волнового числа (кривые 1-3) и берущая начало при 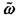 =0,
=0, 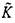 = 0 «гидродинамическая» ветвь решений (4.48) переходит в «фазодинамическую» ветвь, которая при достаточно высоком значении А„ имеет конечный положительный
= 0 «гидродинамическая» ветвь решений (4.48) переходит в «фазодинамическую» ветвь, которая при достаточно высоком значении А„ имеет конечный положительный
инкремент плоского ( 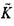 = 0) фронта пламени
= 0) фронта пламени 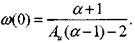 В ча-
В ча-
стности, 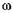 (0) = 0,07 при Аи = 29,
(0) = 0,07 при Аи = 29, 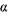 =5.
=5.
Отметим, что характер зависимостей 1 -4 (см. рис. 4.24) не является основанием для установления границы устойчивых искривлений фронта пламени. Исследование быстроразвивающихся возмущений в нарушение условия (4.50), как и уточнение величины 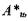 входящей в критерий
входящей в критерий
(4.52), возможно в следующих приближениях теории, учитывающих конечную ширину фронта.
Глава 4. Развитие горения
Таким образом, картина потери устойчивости фронтом пламени в аэрозоле существенно зависит от Аu. Оценим этот параметр для аэрозоля тетралина. Величину Аu можно определить экспериментально в опытах по горению аэрозоля в вертикальной трубе, где относительная скорость фаз us-u1 перед распространяющимся снизу вверх фронтом пламени обусловлена гравитационным оседанием частиц. Анализируя подобные эксперименты с монодисперсным аэрозолем тетралина (ds = 10 -5-2 10 -4 м) можно принять, что характеристики нижнепредельного пламени в аэрозоле (концентрационный предел распространения, околопредельная скорость) зависят только от соотношения горючего и окислителя, поступающих в зону горения. Исходя из этой гипотезы, возмущение относительной доли горючего во фронте пламени можно по аналогии с (4.47) записать в виде
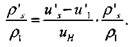
|
(4.52)
Отсюда получаем выражение для флуктуации нормальной скорости распространения пламени
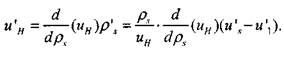 (4.53)
(4.53)
Сравнивая (4.46) и (4.53), получим 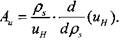
Резкое увеличение нормальной скорости пламени в аэрозоле на величину 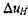 = 0,4 м • с-1 (с 0,1 м • с-1 до 0,5 м • с-1) происходило при относительном изменении пороговой конентрации
= 0,4 м • с-1 (с 0,1 м • с-1 до 0,5 м • с-1) происходило при относительном изменении пороговой конентрации 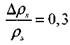 . Отсюда получаем оценку
. Отсюда получаем оценку 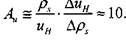
В соответствии с критерием дестабилизации Аи > 2, следовательно, неустойчивость горения нижнепредельных аэрозолей тетралина возможно связать с фазодинамическим эффектом при рассеянии свежей смеси на искривленных и (или) ускоренно движущихся участках фронта пламени.
Таким образом, гидродинамический анализ горения аэродисперсных систем показал, что относительное движение фаз возникает не только в процессе гравитационного оседания частиц пыли, но и в результате вы-
Корольченко А.Я. Процессы горения и взрыва
нужденного рассеяния фаз аэрозоля при искривлении зоны горения. При этом в последнем случае гидродинамика двухфазной системы стимулирует разрушение плоского фронта пламени и, следовательно, переход горения аэрозоля от плосколаминарной формы к турбулентной. Важнейшим выводом из сказанного выше является заключение о неправомерности переноса представлений о постоянстве «нормальной» скорости горения на аэродисперсные системы, поскольку искривление фронта пламени меняет соотношение горючего и окислителя, поступающих в зону горения (фазодинамический эффект), а следовательно, меняется температура горения и скорость движения зоны химической реакции по свежей смеси.
Фазодинамический режим распространения пламени по аэродисперсной системе. Конвективная (турбулентная) форма движения пламени по аэрозолю является наиболее распространенной.
Специфические особенности конвективного горения аэрозолей выражаются следующей упрощенной схемой: расширяющиеся газообразные продукты горения «просеиваются» сквозь решетку частиц свежей смеси, способствуя их разогреву и воспламенению.
Трудности построения математической модели конвективного горения заключаются в том, что оказывается необходимым объединить две сложные сами по себе задачи. Во-первых, требуется иметь четкие представления о микроскопическом («эстафетном») механизме процессов во фронте пламени, и, во-вторых, необходимо учитывать относительное движение (в том числе - случайное вследствие турбулентных флуктуации) фаз аэрозоля, как мощный фактор воздействия на развитие процесса горения аэродисперсной системы. В настоящее время отсутствуют достаточно глубокие исследования каждой из составляющих проблем комплексной задачи конвективного горения, поэтому преждевременно формулировать постановку этой задачи в общем виде. Тем не менее, на основании известных фактов можно в упрощенной постановке решить некоторые задачи конвективного горения, позволяющие сделать по крайней мере качественные выводы о характеристиках пожарной опасности органических аэрозолей.
Ниже, в качестве примера, приводится приближенное решение задачи о распространении «языка» пламени по аэрозолю. Кинограммы распространения пламени по аэрозолям органических веществ (при высокой степени однородности распространения горючего и квазиламинарном те-
Глава 4. Развитие горения
чении фаз) свидетельствуют о повышенной неустойчивости фронта пламени. Это проявляется в значительном увеличении поверхности горения, языкообразном искривлении ведущей части фронта пламени и самоускорении пламени, особенно вблизи нижнего концентрационного предела распространения (НКПР).
Дата добавления: 2015-09-29; просмотров: 1045;
