Пример 9.6

Определить расход воды Q, вытекающей из-под плоского вертикального щита, установленного в канале прямоугольной формы шириной b = 3 м. Глубина воды перед щитом Н =3 м, высота поднятия щита а=0,3 м, глубина воды в нижнем бьефе канала h_н=1,8 м (см. рис. 9.23).

Предположим, что истечение воды из-под щита несвободное. Расход вычисляем по формуле (9.59):

Q= μab ..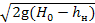

Граничные условия применения данной формулы выражаются отношением

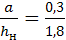
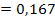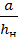, >0,1.

Коэффициент расхода (9.60)

μ=0,6+ 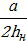= 0,6+ 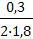= 0,683.

Примем H₀=H,

Q=0,683·0,3·3 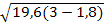=2,98 м³/с

Средняя скорость потока перед щитом

V₀= = = 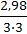0,33 м/c

Скоростной напор 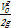= = 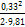0,0056 м.

Скоростной напор из-за своей малой величины не влияет на расход при истечении. Определяем форму сопряжения при истечении.

Глубина сжатого сечения h_с = εа. Коэффициент сжатия ε находим по формуле (9.56):

n= = = 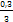0,1 м;

ε= 0,57+ 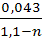=0,57+ 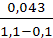=0,613;

h_c=0,613·0,3=0,184 м.

Критическая глубина в прямоугольном канале

h_кр= 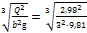=0,465 м.

Фиктивная глубина, сопряженная с h_с = 0,185 м,

h_c''= 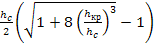= =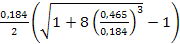0,957 м.

Глубина в нижнем бьефе h_н = 1,8 м; h_н > h_c".

Следовательно, форма сопряжения - затопленный прыжок, истечение несвободное.