Пример 9.5

Определить расход потока воды Q, вытекающего из-под плоского вертикального щита, если перед ним глубина Н= 2,0 м, открытие а = 0,70 м, ширина отверстия b = 3,0 м, глубина в нижнем бьефе h_н = 1 м (см. рис. 9.22).

Находим n= 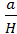= = 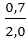0,35.

Определим коэффициент сжатия струи по формуле (9.56):

ε=0,57+ 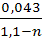=0,57+ 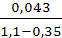=0,627 .

Глубина потока воды в сжатом сечении

h_c = εa= 0,627 • 0,7 = 0,439 м.

Полагаем, что имеет место свободное истечение из-под щита.

При свободном истечении расход определяем по формуле (9.55), считая φ= 1,0:

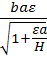
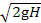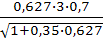
Q_п= = =7,45 м/c.

Находим скорость подхода к щиту:

V₀= = =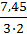1,21 м/с.

Вычисляем число Фруда:

Fr= 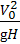= = 0,075 .

Коэффициент скорости по табл. 9.5 φ = 0,96.

Расход воды равен Q = φQ_п = 0,96 • 7,45 = 7,15 м³/с

Уточняем форму сопряжения бьефов при истечении из-под щита.

Критическая глубина в прямоугольном русле

h_кр= = = 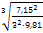0,83 м.

Вычисляем сопряженную с h_с фиктивную глубину h _c ":

h _c "= 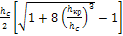= = 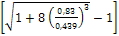1,41 м.

Так как h"_с > h_н , форма сопряжения будет в виде отогнанного прыжка, следовательно, истечение свободное (h_н = 1 м).