Числа в форме с плавающей точкой
В формате представления числе с плавающей точкой каждое число разбивается на две группы цифр. Первая группа цифр называется мантиссой, вторая — порядком. Число представляется в виде произведения X = ±mq± p, где т — мантисса числа, р — порядок числа, q — основание системы счисления.
Для представления числа в формате с плавающей точкой требуется задать знаки мантиссы и порядка, их модули в двоичном коде, а также основание системы счисления (рис. 14.4). Нормальная форма неоднозначна, так как взаимное изменение m и p приводит к «плаванию» точки, чем и обусловлено название этого формата.
| Номер разряда | n-1 | n-2 | n-3 | … | n-r | n-r-1 | n-r-2 | |
| Назначение разрядов | Знак мантиссы | 2n-2 | 2n-3 | … | 2n-r | знак порядка | 2n-r-2 | 20 |
| Мантисса | Порядок |
Рис. 14.4. Формат представления чисел с плавающей точкой
Диапазон и точность представления чисел с плавающей точкой зависят от числа разрядов, отводимых под порядок и мантиссу.
В большинстве компьютеров для упрощения операций над порядками последние приводят к целым положительным числам, применяя так называемый смещенный порядок. Для этого к истинному порядку добавляется целое положительное число — смещение. Например, в системе со смещением 128 порядок -3 представляется как 125 (-3 + 128). Обычно смещение выбирается равным половине представимого диапазона порядков. Отметим, что смещенный порядок занимает все разряды поля порядка (рис. 14.5), в том числе и тот, который ранее использовался для записи знака порядка, т.е. смещенный порядок – это целое число без знака.
| Номер разряда | n-1 | n-2 | n-3 | … | n-r | n-r-1 | n-r-2 | |
| Назначение разрядов | Знак мантиссы | Модуль мантиссы | Смещенный порядок |
Рис. 14.5. Формат числа с плавающей точкой со смещенным порядком
Для 32-разрядных чисел с плавающей точкой возможны следующие диапазоны чисел:
· отрицательные числа между – (1 – 2-24) * 2127 и – 0,5 * 2-128;
· положительные числа между 0,5 * 2-128 и (1 – 2-24) * 2127.
В эту область не включены пять участков:
· отрицательные числа, меньшие чем -(1- 2-24) * 2127 — отрицательное переполнение;
· отрицательные числа, меньшие чем -0,5*2-128 — отрицательная потеря значимости;
· положительные числа, меньшие чем 0,5 * 2-28 — положительная потеря значимости;
· положительные числа, большие чем (1 - 2 -24) * 2127 — положительное переполнение.
Следует также отметить, что числа в формате с плавающей точкой, в отличие от чисел в форме с фиксированной точкой, размещены на числовой оси неравномерно. Значения в начале числовой оси расположены плотнее, а по мере движения вправо — все реже (рис. 14.6). Это означает, что многие вычисления данных в формате с плавающей точкой приводят к результату, который не является точным, то есть представляет собой округление до ближайшего значения, представимого в данной форме записи.
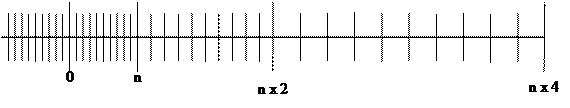 |
Рис. 14.6.Плотность чисел с плавающей точкой на числовой оси
В настоящее время во всех процессорах в обязательном порядке реализован формат чисел с плавающей точкой в соответствии со стандартом IEEE 754.
Дата добавления: 2015-09-28; просмотров: 1037;
