Затухающие гармонические колебания
В реальных системах, участвующих в колебательном движении, всегда присутствуют силы трения (сопротивления):
 ,
, 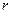 – коэффициент сопротивления;
– коэффициент сопротивления;  – скорость.
– скорость.
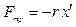 .
.
Тогда ІІ закон Ньютона запишем:


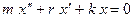
| (2) |
Введем обозначения 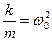 ,
,  , где
, где 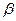 – коэффициент затухания.
– коэффициент затухания.
Уравнение (2) запишем в виде:

| (3) |
Уравнение (3) – дифференциальное уравнение затухающих колебаний.
Его решение 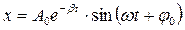 , где
, где
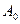 – амплитуда колебаний в начальный момент времени;
– амплитуда колебаний в начальный момент времени;
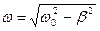 – циклическая частота затухающих колебаний.
– циклическая частота затухающих колебаний.
Амплитуда колебаний изменяется по экспоненциальному закону:
 .
.
 Рис. 11. График x=f(t) Рис. 11. График x=f(t)
| 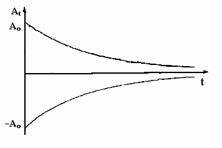 Рис. 12. График At=f(t) Рис. 12. График At=f(t)
|
Характеристики:
1)  – период затухающих колебаний; 2)
– период затухающих колебаний; 2) 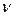 – частота затухающих колебаний;
– частота затухающих колебаний; 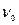 – собственная частота колебательной системы;
– собственная частота колебательной системы;
3) логарифмический декремент затухания (характеризует скорость убывания амплитуды): 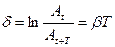 .
.
Дата добавления: 2015-09-28; просмотров: 676;
