Лабораторна робота № 203. ВИЗНАЧЕННЯ КОЕФІЦІЄНТА В’ЯЗКОСТІ РІДИНИ ЗА ДОПОМОГОЮ КАПІЛЯРНОГО ВІСКОЗИМЕТРА ОСТВАЛЬДА
Завдання: визначити коефіцієнт в’язкості рідини за допомогою капілярного віскозиметра Оствальда.
Приладдя: капілярні віскозиметри, ручна помпа, термометр, секун-домір, дистильована вода, досліджувана рідина.
Теоретичний матеріал, який необхідно засвоїти під час підготовки до виконання роботи: головні поняття гідродинаміки, закон Пуазейля, ламі нар-ний і турбулентний потік рідини, гідростатичний тиск (див. також перелік матеріалу до роботи № 201).
Література:
1) § 7.6–7.9, с. 114–124;
2) § 14.2.3, с. 36–38;
3) § 60, с. 186–190;
4) § 28, 31–33, с. 51–52, 55–59.
Опис установки. Експериментальна установка для вимірювання в’язкості рідин (рис. 4) складається з двох однакових віскозиметрів 1 і 2, розміщених у термостаті 3. Нижні резервуари віскозиметрів заповнені дистильованою водою і досліджуваною рідиною. Пампа 4 призначена для піднімання рівня рідини у віскозиметрі. Час протікання рідини через капіляр вимірюють секундоміром 5.
 Ідея роботи та виведення робочої формули. За формулою Пуазейля об’єм рідини V, яка протікає за час t по капіляру з радіусом R під дією гідростатичного тиску rgh,
Ідея роботи та виведення робочої формули. За формулою Пуазейля об’єм рідини V, яка протікає за час t по капіляру з радіусом R під дією гідростатичного тиску rgh,
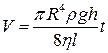 , (1)
, (1)
де l – довжина капіляра; r – густина рідини; h – висота капіляра; h– коефіцієнт в’язкості рідини.
Якщо відомі конструктивні розміри віскозиметра і виміряно значення потрібних величин експеримент-тально, то з (1) можна визначити h. У цій роботі використовують порівняльний метод визначення коефіцієнта в’язкості рідини, забезпечуючи в експерименті сталість величин V,R, h і l. Цього досягають використанням одного віскозиметра або двох ідентичних віскозиметрів з досліджуваною рідиною і рідиною з відомою в’язкістю. Тоді з (1) матимемо
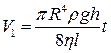 i
i 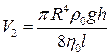 .
.
ОднакV1=V2, тоді, прирівнявши праві частини рівнянь, легко отримати формулу для h:
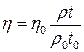 , (2)
, (2)
де hі r – коефіцієнт в’язкості та густина досліджуваної рідини; h0 і r0 – коефіцієнт в’язкості та густина дистильованої води.
Вираз (2) є робочою формулою лабораторної роботи.
Формулу Пуазейля (1) можна вивести з таких міркувань. Нехай по трубі радіусом R і довжиною l (рис. 5) тече в’язка рідина зі швидкістю v. Протікання забезпечує різниця сил тиску на торцях циліндра F1 та F2. Водночас між шарами рідини виникає сила внутрішнього тертя
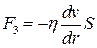 , (3)
, (3)
 де dv/dr – градієнт швидкості в напрямі радіуса; S=2prl – площа бокової поверхні циліндричного шару рідини. Оскільки v=const, то F1–F2=F3, або
де dv/dr – градієнт швидкості в напрямі радіуса; S=2prl – площа бокової поверхні циліндричного шару рідини. Оскільки v=const, то F1–F2=F3, або
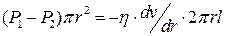 . (4)
. (4)
Проінтегруємо цю рівність, отримаємо
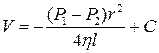 . (5)
. (5)
Сталу інтегрування С визначаємо з умови, що біля стінок труби v = 0. Тоді
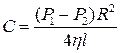 , а
, а 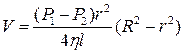 . (6)
. (6)
Формула (6) свідчить, що швидкість рідини розподілена в напрямі, перпендикулярному до осі труби, за квадратичним законом і є максимальною на осі труби.
Визначимо тепер об’єм рідини, яка протікає через трубу за одиницю часу. Для цього розіб’ємо поперечний переріз труби на кільця товщиною dr з радіусом r. Тоді dV=2pvrdr. Після інтегрування
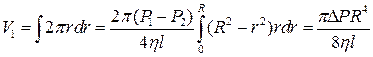 ,
,
a за час t – 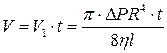 . (7)
. (7)
Це формула Пуазейля для ламінарної течії рідини в капілярній трубці.
Дата добавления: 2015-09-02; просмотров: 1406;
