Механизм образования касательной силы тяги

При заданном токе нагрузки тяговый электродвигатель развивает на валу вращающий момент 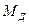(рис. 1.1), равный по величине

,

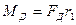где 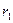- радиус шестерни, м;

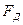- окружное усилие зубчатой передачи, Н.

Окружное усилие зубчатой передачи можно выразить обратно через вращающий момент

.

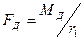Частоту вращения вала двигателя и шестерни обозначим 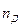- число оборотов в минуту.

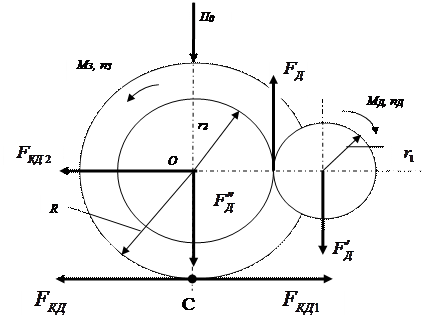
Рис. 1.1. Схема образования касательной силы тяги

Действуя на радиусе ведомого зубчатого колеса 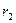, сила 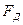вызовет реакцию в центре колеса - 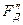. Возникнет пара сил 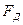, , 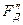которая при вращении создает момент 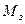, несколько меньший чем момент 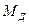, за счет трения в зубьях. Из этого следует, что

,

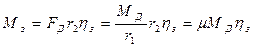где 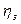- КПД, учитывающий потерю мощности в зубчатой передаче и моторно-осевых подшипниках тягового электродвигателя;

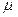- передаточное число.

Зубчатое колесо будет иметь частоту вращения 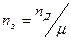, а вместе с ним будет вращаться движущее колесо вокруг центра О. В результате действия вращающего момента 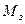и нагрузки от колеса на рельс 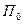возникнет касательная реакция от рельса на колесо 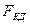и пара сил на движущем колесе 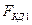, 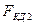с моментом

,

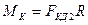где 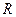- радиус колеса.

Реакция 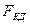представляет собой силу сцепления колеса с рельсом, приблизительно равную

,

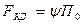где 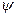- статический коэффициент трения. Благодаря реакции 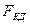колесо будет
стремиться вращаться вокруг мгновенного центра вращения С, что приведёт к качению по рельсам.

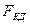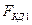По закону действия и противодействия силы и взаимно уравновешиваются. Сила 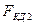остается неуравновешенной иявляется внешней для локомотива, так как она действует на колесо, которое закреплено (благодаря сцеплению) на рельсе в точке мгновенного центра вращения С и составляет вместе с рельсами единую систему - внешнюю по отношению к локомотиву. Следовательно, сила 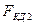является движущей силой локомотива. Так как для удобства расчетов условились относить все силы, определяющие движение поезда, к ободам движущих колес, то касательной силой тяги считают силу 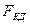, равную по величине силе 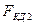. Таким образом,

,

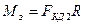откуда имеем касательную силу тяги, создаваемую одним двигателем:

.

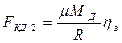Касательная сила тяги всего локомотива 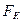будет равна сумме сил всех движущих колес, т. е.

.

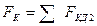Качение колес приводит к поступательному движению локомотива со скоростью

,

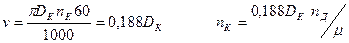где 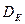- диаметр колеса, м;

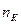- частота вращения колеса, об/мин: .

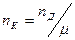Измерить 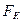практически невозможно. Динамометром измеряют силу тяги на сцепке первого к локомотиву вагона 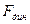, и называют ее динамометрической. Сила 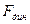меньше силы 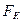на величину сил сопротивления движению и сил инерции самого локомотива.

Сила сцепления колес с рельсами

Величина момента М, который может быть приложен к ведущему колесу (ведущей оси) локомотива меняется в зависимости от изменений режима движения и режима работы энергетической установки локомотива.

Нов любом случае сила трения покоя (при отсутствии скольжения), которая является силой реакции на действующий момент, не может превосходить какого-то предельного значения, зависящего от условий трения (сцепления):

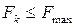, (2. 1)

Это условие называют основным (или первым) законом локомотивной тяги.

Чтобы увеличить силу тяги (см. рис. 1.1), нужно увеличить величину вращающего момента, чтобы уменьшить - соответственно снизить его величину. Практически наиболее важной и чаще встречающейся потребностью в эксплуатации бывает необходимость увеличения силы тяги локомотива на отдельных этапах его движения с поездом (в моменты трогания поезда с места, его разгона, при движении на крутых подъемах и т.п.). Однако безграничное увеличение вращающего момента, приложенного к ведущей оси, невозможно. Дело в том, что, как было показано выше, сила тяги возникает как реакция на вращающий момент при условии отсутствия скольжения в точке С, то есть при наличии между колесом и рельсом необходимой для этого величины силы трения.

Сила трения скольжения по закону Кулона-Амонтона прямо пропорциональна величине силы, прижимающей трущиеся поверхности друг к другу. В нашем случае это нагрузка от колеса на рельс 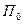. Известно также, что величины силы трения при отсутствии проскальзывания (так называемая сила трения покоя) и соответствующего ей коэффициента трения покоя 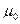больше, чем соответственно величины силы и коэффициента трения при начавшемся скольжении.

Стало быть, максимальная величина силы трения между колесом и рельсом при отсутствии скольжения равна 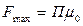. И,следовательно, наибольшее возможное значение силы тяги, как уже было отмечено выше, не может быть больше максимальной величины силы трения между колесом и рельсом, то есть .

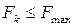Реальный процесс взаимодействия колеса, создающего силу тяги, и рельса более сложен, так как поверхности колеса и рельса не плоские, а криволинейные. Поэтому в контакте колеса и рельса имеют место трение и скольжение и в поперечном направлении.

Ихотя все основано именно на трении, процесс реального взаимодействия ведущего колеса и рельса на железнодорожном транспорте называют сцеплением и величину максимальной силы тяги называют силой тяги по условиям сцепления ведущих колес с рельсами (или просто - «по сцеплению»), а само выражение неравенства - ограничением силы тяги по сцеплению.

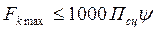, (2. 2)

где 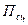- сцепной вес, кН;

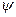- коэффициент сцепления колеса с рельсом.

Неравенство (2.2)и является конкретным выражением основного закона локомотивной тяги. Важно обратить внимание на то, что и при формулировке закона, и в этом его конкретном выражении отсутствуют указания на тип локомотива и мощность энергетической установки. Этот закон одинаково ограничивает наибольшую величину силы тяги автономных и неавтономных локомотивов по условию сцепления ведущих колес и рельсов независимо от типа и мощности самого локомотива.

Процесс взаимодействия ведущего колеса и рельса при создании силы тяги очень сложен и егопротекание зависит от множества переменных факторов. Взаимодействие зависит от величин нагрузок, передаваемых на рельс колесом: вертикальной силы нажатия и вращающего момента, а также от скорости движения, упругих свойств материалов колеса и рельса, состояния и износа их рабочих поверхностей и ряда других, в том числе и случайных, условий и обстоятельств.

Как уже неоднократно подчеркивалось выше, основным физическим фактором, обеспечивающим возможность поступательного движения ведущего колеса любого колесного транспортного средства, является трение между колесом и дорогой. Трение с точки зрения физики складывается из целого комплекса различных физико-механических процессов, протекающих в поверхностных слоях контактирующих тел.

Различают два основных вида взаимодействия при трении: механическое и молекулярное. Механическое взаимодействие характеризуется взаимным проникновением контактирующих точек вследствие деформации тел при высоких удельных давлениях. Молекулярное взаимодействие связано с взаимным проникновением контактирующих твердых тел, вызываемым неуравновешенным состоянием атомов на их поверхностях.

Такой двойственный молекулярно-механический принцип обычно и принимают в качестве «обобщенной» теории трения.

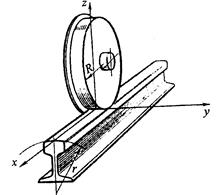
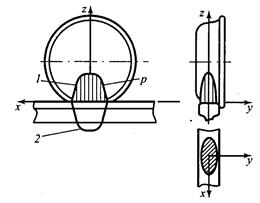
Рабочие поверхности колеса подвижного состава и железнодорожного рельса (рис. 2.1) в зоне контакта между ними являются цилиндрическими, так как средняя часть стандартного профиля головки отечественных рельсов очерчена по радиусу (r = 300мм), а коническую поверхность катания колеса, радиус круга катания R которого для стандартных колес локомотивов имеет величину R = 525 мм, если диаметр колес 1050 мм, или R = 625 мм (при диаметре - 1250 мм), в зоне контакта с рельсом можно посчитать так же за цилиндрическую, так как образующие конусной поверхности бандажа при качении перпендикулярны вертикальной оси рельса из-за установки его подошвы с уклоном 1:20 (подуклонки). Контакт двух прижатых друг к другу цилиндров с перпендикулярными осями (z и y) осуществляется в точке, если цилиндры абсолютно жесткие, то есть недеформируемые.

В действительности же при контакте под нагрузкой оба тела - колесо и рельс - деформируются. Поэтому встатическом состоянии, ввиду того, что и колесо, и рельс не являются абсолютно жесткими и вследствие их деформации под действием вертикальной нагрузки вместо точки контакта С, подразумевавшейся на рис. 2.1 при абсолютно жестких колесе и рельсе, образуется контактная площадка (рис. 2.2). Механические свойства материала (стали) контактирующих тел (колеса и рельса) приблизительно одинаковы, но вследствие различия радиусов контактирующих цилиндров контактная площадка двух цилиндров теоретически имеет форму не круга, а эллипса.

Величина контактной площадки между колесом локомотива и рельсом имеет порядок (по площади) 300—400 мм². Именно через такие небольшие по величине площади передаются на рельсы нагрузки от колес подвижного состава, которые на отечественных железных дорогах могут достигать значений П=125 кН. При этом средние по площади величины напряжений сжатия в колесе и рельсе составляют 300—400 МПа, что превышает величину предела упругости стали.

Наибольшая величина нормального напряжения сжатия 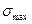имеет место в центре контактной площадки, где величина вертикальных деформаций колеса и рельса наибольшая. Теоретически она в полтора раза выше среднего напряжения по площадке. И, следовательно, даже при статическом контакте колеса и рельса в их материалах возникают не только упругие, но и пластические остаточные деформации, которые приводят к их постепенному износу.

Таким образом, вся контактная площадка между колесом и рельсом в целом как быт делится на две различные части: зона чистого качения, в которой практически не действуют силы трения, зоны сцепления, где взаимодействие колеса и рельса определяется трением.

Волокна поверхности рельса в пределах контактной площадки еще более растягиваются под действием касательной силы от колеса. В процессе перекатывания колеса перемещается с ним и контактная площадка. При этом сжатые в передней части площадки волокна колеса начинают восстанавливать свою форму, то есть вследствие упругости материала постепенно разжимаются. Одновременно растянутые волокна на поверхности рельса вследствие своей упругости также стремятся восстановить форму, то есть вернуть свое прежнее нерастянутое состоянию.

Очевидно, что при этом в пределах контактной площадки неизбежно происходит относительно смещение (упругое проскальзывание) растягивающихся (ранее сжатых) волокон колеса и сжимающихся (прежде растянутых) волокон материала рельса.

Таким образом, в передней части контактной площадки благодаря упругости деформаций имеет место качение колеса без относительного смещения поверхностей колеса и рельса. А в задней по ходу движения части контактной площадки происходит упругое смещение (проскальзывание) поверхностных волокон колеса и рельса относительно друг друга с какой-то скоростью .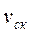

При дальнейшем увеличении момента и действующей от колеса на рельс силы величина деформаций (растяжения и сжатия) волокон на поверхности колеса и рельса увеличивается, и упругое их смещение переходит в относительное проскальзывание, при котором величина силы трения (при движении) уменьшается по сравнению с силой трения покоя и уменьшается сила сцепления между колесом и рельсом. Сцепление колеса и рельса нарушается, оно сопровождается относительным проскальзыванием колеса. Чем больше скорость движения, тем быстрее сменяются точки поверхности колеса, попадающие в область контактной площадки, тем быстрее протекают процессы упругих деформаций волокон поверхности катания колеса, что связано с увеличением скорости относительного скольжения 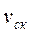колеса по рельсу.

Таким образом, создание и реализация силы тяги на основе сцепления колеса и рельса всегда сопровождаются большим или меньшим относительным упругим проскальзыванием колес. Чем больше величина реализуемой силы тяги, тем больше величина относительного проскальзывания. Именно это проскальзывание и является одной из причин износа поверхности катания ведущих колес и рабочей поверхности рельсов.

При увеличении скольжения может наступить потеря сцепления - боксование.

На характер протекания процессов в зонах контакта ведущих колес локомотивов с рельсами также влияют:

- конусность профиля поверхности катания бандажей и наклонная установка рельсов. Значительное влияние оказывают отклонения от начальной формы поперечных профилей колеса и рельса, возникающие вследствие их износа. Из-за проката бандажей форма, расположение и размеры контактной площадки меняются.

- наличие посторонних веществ между колесами и рельсами (пыль, грязь, листья и другие остатки растительности, следы смазочных материалов и атмосферные осадки и явления (дождь, снег, иней, лед), которые, играя роль своего рода смазки, могут заметно снижать величину коэффициента трения между ними.

Как было сказано выше, сила сцепления зависит от коэффициента сцепления. В расчетах используют расчетный коэффициент сцепления 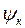, величина которого определяется эмпирически.

1. На величину коэффициента сцепления влияет степень относительного проскальзывания (или относительной скорости проскальзывания 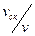)колеса по рельсу в точке контакта. При росте 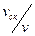величина коэффициента сцепления снижается. Это может привести к значительной потере сцепления – вплоть до боксования. Следовательно, для повышения тяговых возможностей локомотивов необходимо контролировать скорость относительного проскальзывания колес.

Такие системы контроля позволяют не только защитить локомотив от возможности боксования, но и гарантировать реализацию расчетных величин его силы тяги.

2. Эта же тенденция снижения коэффициента сцепления наблюдается при увеличении скорости поступательного движения, когда продолжительность времени взаимного молекулярного контакта частиц колеса и рельса сокращается.

3. Величина коэффициента сцепления зависит от состояния поверхностей колеса и рельса, наличия окислов на этих поверхностях и загрязнений между ними.

Например, известно, что после сильных дождей, хорошо очищающих поверхности рельсов сцепление колес с рельсами улучшается. Наоборот, при незначительных осадках (небольшой дождь или снег, роса, иней) частицы пыли и растительных остатков, находящиеся на поверхности рельсов, увлажняясь, образуют пленку, тонкий слой грязи, что ухудшает сцепление колес с рельсами. В то же время, в частности, очевидно, что подача сухого кварцевого песка в зону контакта колес и рельсов существенно увеличивает величину коэффициента сцепления.

Поэтому все современные локомотивы имеют так называемые песочные системы с бункерами для хранения запаса сухого песка и форсунками для распыливания его в зону контакта ведущих колес с рельсами.

4. Взаимодействие колеса и рельса и, следовательно, значение коэффициента сцепления зависят от степени износа (изменения геометрической формы) контактирующих поверхностей.

5. Устойчивость сцепления колес и рельсов зависит и от конструкции экипажа локомотива и типа его тягового привода. При групповом приводе, когда возможность боксования отдельных колесных пар исключается, величина коэффициента сцепления локомотива более стабильна. Можно отметить влияние некоторых конкретных элементов конструкции и эксплуатации:

а) так как величина суммарной силы тяги локомотива ограничена его лимитирующей (наиболее разгруженной при движении) колесной пары. Фактический коэффициент сцепления 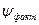локомотива, зависит от величины коэффициента использования его сцепного веса 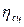. Коэффициентом использования сцепного веса 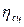называют отношение нагрузок от ведущих колесных пар локомотива на рельсы: величины нагрузки колесной пары, наиболее разгруженной при реализации силы тяги, 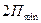к средней нагрузке всех ведущих колесных пар 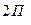, то есть 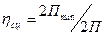. Можно считать, что .

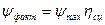б) увеличение диаметра колес локомотива несколько увеличивает размеры контактной площадки между колесом и рельсом, что увеличивает и коэффициент сцепления .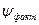

в) увеличение нагрузки на колесную пару и, как следствие, увеличение удельных давлений в зоне контакта в результате снижают величину коэффициента сцепления, так как пластические деформации в зоне контакта растут и играют роль своеобразной смазки, снижающей трение покоя;

г) при кратной тяге у второго локомотива может быть реализован более высокий коэффициент сцепления, сказывается эффект «зачистки» поверхности рельсов при прохождении их первым локомотивом.

Надо заметить, что факторы, отмеченные в пунктах б) и в), имеют лишь теоретическое значение, поскольку различия диаметров колес и осевых нагрузок у современных магистральных локомотивов относительно невелики, и поэтому влияние этих факторов (диаметра и нагрузки), если и проявляется на практике, то незначительно.

Таким образом, физический коэффициент сцепления зависит от трех групп факторов: от конструкции локомотива и состояния его колесных пар, от конструкции и состояния пути и от атмосферных условий.

Максимальные по величине значения коэффициента сцепления в конкретных условиях могут быть получены при сухих рельсах и при подаче песка.

Величинакоэффициента сцепления, принимаемая за расчетную - расчетный коэффициент сцепления 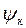- имеет очень важное значение для организации работы железных дорог. От правильного выбора этого значения зависят установление весовых норм поездов и эффективность использования тяговых возможностей локомотивов и надежность их эксплуатации.

Правилами тяговых расчетов для поездной работы установлены следующие эмпирические формулы для определения :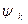

5) электровозы постоянного тока:

;

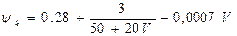6) электровозы переменного тока:

;

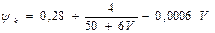7) тепловозы серии ТЭ10:

;

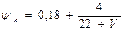8) остальные тепловозы (производства стран СНГ)

.

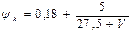Здесь V – скорость движения локомотива, км/ч.