Приток к бесконечным цепочкам и кольцевым батареям скважин

При разработке месторождений добывающие скважины бурят не произвольно, а в каком – либо порядке. Обычно скважины располагают рядами, кольцевыми батареями или более сложным образом. Ознакомимся с широко применяемым при проектировании разработки нефтяных месторождений методом эквивалентных фильтрационных сопротивлений, предложенным Ю. П. Борисовым и основанным на аналогии движения жидкости в пористой среде с течением электрического тока в проводниках. Рассмотрим без вывода задачу о притоке жидкости к одиночной скважине, расположенной между двумя непроницаемыми граница расстояние между которым 2s и на расстоянии L от прямолинейного контура питания. Пусть на контуре питания задано постоянное давление p_k, на забое скважин — давление p_c, (рис. 4.7). Требуется определить дебит.

Рис. 4.7 . Обоснование метода фильтрационных сопротивлений Ю. П. Борисова

Заменим исходный фильтрационный поток на два более простых потока. У прямолинейного контура питания движение близко к плоскопараллельному. Среднее давление на уровне скважины между непроницаемыми границами p₁. Тогда дебит в таком фильтрационном потоке определяется по формуле притока к галере

.

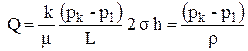(4.20)

Величина r называется внешним фильтрационным сопротивлением и определяется по формуле:

.

(4.21)

Второй фильтрационный поток происходит вблизи скважины, где характер движения близок к плоскорадиальному. При этом фильтрация происходит от фиктивного контура питания радиусом R₁ с давлением p₁ к скважине. Дебит такого фильтрационного потока рассчитывается по формуле Дюпюи:

.

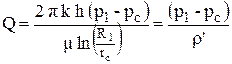(4.22)

Радиус фиктивного контура питания можно найти из точного решения. Он оказался равным R₁ = s/p. Величина r¢ называется внутренним фильтрационным сопротивлением и определяется по формуле:

.

(4.23)

Таким образом, приток жидкости к такой скважин можно представить схемой эквивалентных фильтрационных сопротивлений, показанной на рис. 4.8 Аналогом объемного расхода Q служит сила тока, а аналогом разности давлений — разность электрических потенциалов. Дебит скважины находится по закону Ома для данной схемы:

.

(4.24)

Рис. 4.8 . Схема притока к конечной цепочке скважин

Используя метод отражения можно перейти от элемента фильтрационного потока к бесконечной цепочке скважин или, с некоторой ошибкой, к цепочке из n скважин. Тогда дебит такой цепочки скважин будет равен:

.

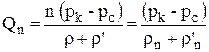(4.25)

Здесь r_n и r_n¢ внешнее и внутреннее сопротивление цепочки из n скважин находятся по формулам:

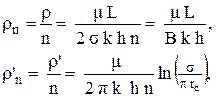
(4.26)

где B ширина всей цепочки скважин.

Рис. 4.9 . Схема притока к кольцевой батарее скважин

Рассмотрим применение метода Ю. П. Борисовым для одного элемента и всей кольцевой батареи из n скважин Рис. 4.9. Заменим элемент кольцевой батареи скважин, который на рисунке выделен двумя непроницаемыми границами, на два более простых потока. Оба этих потока будут плоскорадиальными. Сама схема эквивалентных фильтрационных сопротивлений останется такой же, что и для элемента цепочки скважин, но формулы расчета внешнего фильтрационного сопротивления изменяться:

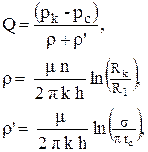
(4.27)

где s = π R₁/n.

Для всей кольцевой батареи:

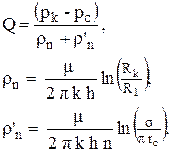
(4.28)

1.5.