Истечение через малые отверстия в тонкой стенке при постоянном напоре
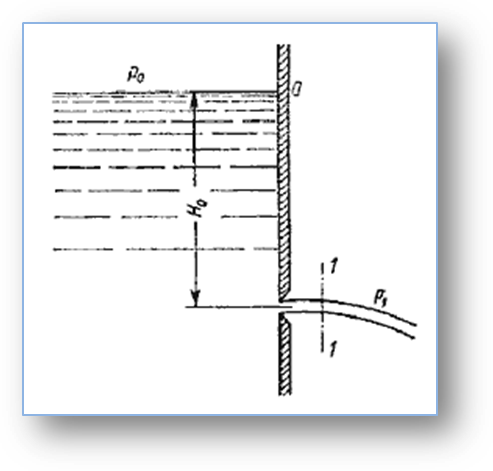
Рассмотрим большой резервуар с жидкостью под давлением Р0, имеющий малое круглое отверстие в стенке на достаточно большой глубине Н0 от свободной поверхности (рис. 2).
|
Рис. 2. Истечение из резервуара через малое отверстие
Жидкость вытекает в воздушное пространство с давлением Р1. Вытекающая струя претерпевает сжатие (рис. 1).
На некотором расстоянии от отверстия, близком к  , вытекающая струя получает сжатие поперечного сечения, характеризуемое уменьшением диаметра и сечения струи.
, вытекающая струя получает сжатие поперечного сечения, характеризуемое уменьшением диаметра и сечения струи.
Пусть отверстие имеет форму, показанную на рис. 3,а, т.е. выполнено в виде сверления в тонкой стенке без обработки входной кромки или имеет форму, показанную на рис. 3,б, т.е. выполнено в толстой стенке, но с заострением входной кромки с внешней стороны. Струя, отрываясь от кромки отверстия, несколько сжимается (рис. 3, а). Такое сжатие обусловлено движением жидкости от различных направлений, в том числе, и от радиального движения по стенке, к осевому движению в струе.
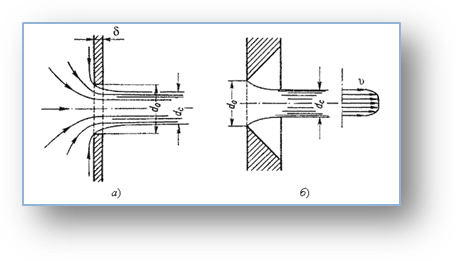
Рис. 3. Истечение жидкости через малое круглое отверстие в тонкой стенке
Отношение площади струи в сжатом сечении к площади отверстия называется коэффициентом сжатия струи: 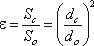 , где Sс и Sо - площади поперечного сечения струи и отверстия соответственно; dси dо - диаметры струи и отверстия соответственно.
, где Sс и Sо - площади поперечного сечения струи и отверстия соответственно; dси dо - диаметры струи и отверстия соответственно.
Значение коэффициента сжатия зависит от характера деформации потока. Если струя имеет равное сжатие по всему периметру, то сжатие называется полным, в противном случае сжатие называется неполным. Сжатие также может быть совершенным и несовершенным. Совершенным сжатием называется такое, при котором ни свободная поверхность, ни близлежащие стенки не влияют на сжатие струи[1].

Скорость истечения жидкости через отверстие:

где Н - напор жидкости, определяется как
 φ- коэффициент скорости:
φ- коэффициент скорости:
где α - коэффициент Кориолиса;
ζ - коэффициент сопротивления отверстия.
Расход жидкости определяется как произведение действительной скорости истечения на фактическую площадь сечения: 
 Произведение ε и φпринято обозначать буквой μ(мю) и называть коэффициентом расхода, т.е. μ = εφ.
Произведение ε и φпринято обозначать буквой μ(мю) и называть коэффициентом расхода, т.е. μ = εφ.
В итоге получаем расход:
где ΔР- расчетная разность давлений, под действием которой происходит истечение.
Значение коэффициента сжатия ε, сопротивления ζ, скорости φ и расхода μ для круглого отверстия можно определить по эмпирически построенным зависимостям. На рис. 4 показаны зависимости коэффициентов ε, ζ и μ от числа Рейнольдса, подсчитанного для идеальной скорости: 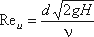 , где ν - кинематическая вязкость.
, где ν - кинематическая вязкость.
При истечении струи в атмосферу из малого отверстия в тонкой стенке происходит изменение формы струи по её длине, называемое инверсией струи (рис. 5). Обуславливается это явление в основном действием сил поверхностного натяжения на вытекающие криволинейные струйки и различными условиями сжатия по периметру отверстия. Инверсия больше всего проявляется при истечении из некруглых отверстий.

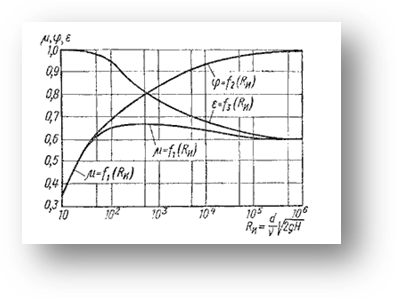
| Рис. 4. Зависимость ε, φ и μот числа Re | Рис. 5. Инверсия струй |
Дата добавления: 2015-09-23; просмотров: 1988;
