На підставі (5.3) рівняння (5.4) запишемо у вигляді
s23dl=s12dl+s13dlcosq, або
s23=s12+s13cosq, (5.5)
звідки
 . (5.6)
. (5.6)
 Якщо σ23>σ12 і │σ23–σ12│<σ13, то крайовий кут 0<θ<π/2, оскільки 0<cosθ<1. За умови 0<θ<π/2 рідина частково змочує поверхню. Якщо ж q=0, то рідина повністю змочує поверхню, розтікаючись по ній молекулярним шаром.
Якщо σ23>σ12 і │σ23–σ12│<σ13, то крайовий кут 0<θ<π/2, оскільки 0<cosθ<1. За умови 0<θ<π/2 рідина частково змочує поверхню. Якщо ж q=0, то рідина повністю змочує поверхню, розтікаючись по ній молекулярним шаром.
Якщо σ23<σ12 і │σ23–σ12│<σ13, то 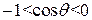 і крайовий кут π/2<θ<π. Це умова незмочування рідиною поверхні стінки посудини. Умови змочування і незмо-чування зумовлюють різну форму поверхні рідини біля стінки посудини (рис. 5.3).
і крайовий кут π/2<θ<π. Це умова незмочування рідиною поверхні стінки посудини. Умови змочування і незмо-чування зумовлюють різну форму поверхні рідини біля стінки посудини (рис. 5.3).
Коефіцієнт поверхневого натягу залежить від різновиду рідини і середовища, з яким вона контактує. Для більшості рідин з підвищенням температури σ лінійно зменшується, а за критичної температури σ=0. Наближену залежність σ=f(T)для температур Т<Тк дає емпірично визначене рівняння
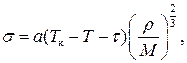 (5.7)
(5.7)
де а – стала, Тк – критична температура; r – невелика поправка в розмірності температури; ρ – густина; М – молярна маса рідини. Як бачимо, коефіцієнт поверхневого натягу лінійно зменшується з підвищенням температури. В довідниках, як звичайно, наведене значення σ за кімнатної температури, коли рідина межує зі своєю парою.

 Якщо поверхня рідини не є плоскою, то сили поверхневого натягу зумовлюють виникнення додаткового тиску під викривленою поверхнею рідини. Переконатись у наявності додаткового тиску, зумовленого кривизною поверхні рідини, можна, виконавши нескладний експеримент з мильними бульбашками. Якщо на кінцях скляної трубки (рис. 5.4) видути бульбашки А і В різного діаметра і полишити систему саму на себе, то можна спостерігати, що бульбашка В меншого діаметра завжди зменшу-ватиметься, а буль-башка А більшого діаметра збільшуватиметься. Отже, тиск усе-редині В більший, ніж тиск усередині А, радіус кривини поверхні якої є більшим.
Якщо поверхня рідини не є плоскою, то сили поверхневого натягу зумовлюють виникнення додаткового тиску під викривленою поверхнею рідини. Переконатись у наявності додаткового тиску, зумовленого кривизною поверхні рідини, можна, виконавши нескладний експеримент з мильними бульбашками. Якщо на кінцях скляної трубки (рис. 5.4) видути бульбашки А і В різного діаметра і полишити систему саму на себе, то можна спостерігати, що бульбашка В меншого діаметра завжди зменшу-ватиметься, а буль-башка А більшого діаметра збільшуватиметься. Отже, тиск усе-редині В більший, ніж тиск усередині А, радіус кривини поверхні якої є більшим.
Розглянемо сферичну краплину рідини, умовно перерізавши її площиною на дві половини, розмежовані колом радіуса R (рис. 5.5). На кожен елемент довжини кола Δl діятимуть сили поверхневого натягу fi = σΔli вздовж дотичних до поверхні сфери. Сума цих сил дає рівнодійну f, яка перпендикулярна до площини перерізу:
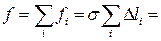 s×2pR. (5.8)
s×2pR. (5.8)
Тоді тиск, зумовлений дією сили f,
 , (5.9)
, (5.9)
де S – площа перерізу сферичної краплини.
Якщо поверхня рідини відрізняється від сферичної, то кривину її поверхні описують через усереднений радіус кривини Rс:
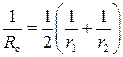 , (5.10)
, (5.10)
де r1 і r2 – радіуси кривизни поверхні у двох взаємноперпендикулярних площинах, що проходять через нормаль до поверхні. Радіус кривизни r додатний, якщо центр кривизни міститься всередині рідини і від’ємний, якщо центр кривини міститься поза нею. Для такої поверхні
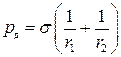 . (5.11)
. (5.11)
Вираз (5.11) називають формулою Лапласа для додаткового тиску, зумовленого кривиною поверхні рідини. Сили додаткового тиску завжди напрямлені до центра кривини поверхні.
Для сферичних поверхонь r1=r2=R і вираз (5.11) перетворюється у (5.9). Для циліндричної поверхні r1 =R, а r2=∞, тоді
рд= 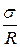 . (5.12)
. (5.12)
За умови плоскої поверхні r1=r2=∞, отже, рд=0. Під плоскою поверхнею рідини додаткового тиску нема.
 Виникнення додаткового тиску під викривленою поверхнею рідини дає змогу пояснити таке явище, як капілярність. У достатньо вузьких посудинах (трубки малого перерізу, мікропори тощо) відстань між поверхнями, що обмежують рідину, сумірна з радіусом кривини її поверхні. За цих умов вільна поверхня рідини утворює меніск. Якщо рідина змочує поверхню капіляра, то меніск має увігнуту форму, якщо не змочує, – то опуклу (рис. 5.6).
Виникнення додаткового тиску під викривленою поверхнею рідини дає змогу пояснити таке явище, як капілярність. У достатньо вузьких посудинах (трубки малого перерізу, мікропори тощо) відстань між поверхнями, що обмежують рідину, сумірна з радіусом кривини її поверхні. За цих умов вільна поверхня рідини утворює меніск. Якщо рідина змочує поверхню капіляра, то меніск має увігнуту форму, якщо не змочує, – то опуклу (рис. 5.6).
Під увігнутою поверхнею рідини (А) виникає від’ємний додатковий тиск pц=2σ/R. Дія сил додаткового тиску спричинює підняття рівня рідини в капілярі на висоту h, за якої гідростатичний тиск ρgh зрівноважить додатковий. Справді, згідно з законом Паскаля, тиски в точках 1 і 2 (рис. 5.6) однакові: p1=p2. Проте,
p1=p0+rg(l+h)+pм– 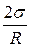 , a p2=p0+rgl+pм,
, a p2=p0+rgl+pм,
де рм – молекулярний тиск; р0 – атмосферний тиск. Тоді
p0+rg(l+h)+pм – 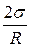 = p0+rgl+pм,
= p0+rgl+pм,
звідки
ρgh=2σ/R, (5.13)
де ρ – густина рідини; g – прискорення вільного падіння.
Якщо змочування неповне, то
R=r/cos θ, (5.14)
де R – радіус кривини меніска; r – радіус капіляра; θ – крайовий кут. Тоді (5.13) зведемо до вигляду
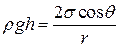 , (5.15)
, (5.15)
звідки
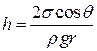 . (5.16)
. (5.16)
Вираз (5.16) дає змогу обчислити висоту підняття рідини в капілярі над рівнем рідини в посудині. За умови змочування (π/2<θ<π/2, cosθ>0) отримаємо додатні значення h, тоді як у разі незмочування (π/2<θ<π, cosθ<0) h буде від’ємним.
Обчислимо тепер висоту піднімання рідини в циліндричному капілярі (дві паралельні пластини, відстань між якими d~R). Умову рівноваги стовпа рідини за цих умов запишемо у вигляді
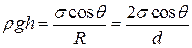 . (5.17)
. (5.17)
Тоді
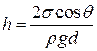 . (5.18)
. (5.18)
Явища, зумовлені поверхневим натягом рідин відіграють важливу роль у природі й техніці. Зокрема, вони пояснюють піднімання води з ґрунту по стовбурах дерев, дію фільтрувального паперу, збагачення руд флотацією, дію ефективних мийних засобів тощо.
Дата добавления: 2015-09-02; просмотров: 834;
