Структурные сетки и графики частот вращения шпинделей

Для кинематических расчетов коробок скоростей в станкостроении применяют два метода: аналитический и графоаналитический. Оба метода позволяют находить величины передаточных отношений передач, входящих в коробку скоростей. Однако, как правило, используют графоаналитический метод. Достоинством его является то, что он позволяет быстро находить возможные варианты решения, дает большую наглядность. При графоаналитическом методе последовательно строят структурную сетку и график частоты вращения.

Структурная сетка дает ясное представление о структуре привода станка. По данной сетке можно проследить связи между передаточными отношениями групповых передач (групповой передачей называют совокупность передач между двумя последовательными валами коробки скоростей). Вместе с тем структурная сетка не дает конкретных значений этих величин. Структурная сетка содержит следующие данные о приводе: число групп передач, число передач в каждой группе, относительный порядок конструктивного расположения вдоль цепи передач, порядок кинематического включения групп, диапазон регулирования групповых передач и всего привода, число частот вращения ведущего и ведомого валов групповой передачи.

График частоты вращения позволяет определить конкрет-

ные величины передаточных отношений всех передач привода и частоты вращения всех его валов. Его строят в соответствии с кинематической схемой привода. При разработке кинематической схемы коробки скоростей станка с вращательным главным движением должны быть известны: число ступеней частоты вращения 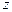шпинделя, знаменатель геометрического ряда 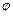, частоты вращения

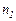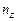шпинделя от до и частота вращения электродвигателя.

Число ступеней частоты вращения 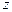шпинделя равно произведению числа передач в каждой группе .

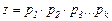При заданном (или выбранном) числе 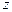число групп передач, число передач в каждой группе и порядок расположения групп можно выбирать различными. Этот выбор и определяет в основном и определяет конструкцию коробки скоростей.

В станках с изменением частоты вращения шпинделя по геометрическому ряду передаточные отношения передач в группах образуют геометрический ряд с знаменателем 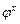, где 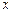- целое число, которое называют характеристикой группы.

Во избежание чрезмерно больших диаметров зубчатых колес в коробках скоростей, а также для нормальной их работы установлены следующие предельные передаточные отношения между валами при прямом зацеплении: 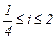; отсюда наибольший диапазон регулирования групповой передачи будет

.

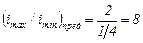Отношение 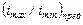имеет наибольшую величину для последней переборной группы привода. Следовательно, для коробок скоростей

,

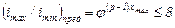где 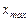наибольший показатель для последней переборной группы; 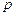- число передач в этой группе.

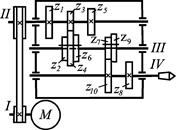
Рассмотрим построение структурной сетки и графика частот вращения для коробки скоростей, кинематическая схема которой показана на рис. 4, а. Для принятого конструктивного варианта при

а

б в

г д

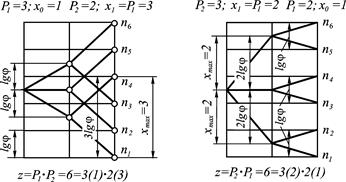
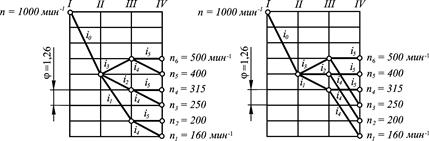
Рис. 4. Кинематическая схема (а), структурные сетки (б, в) и графики частоты вращения коробки скоростей (г, д) на шесть ступеней

вода возможны два варианта структурной формулы: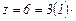

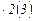и 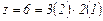. В первом случае основной группой будет первая в конструктивном отношении группа передач, а первой переборной – вторая группа передач; для второго случая наоборот.

На рис. 4, а, б показаны структурные сетки, приведенных структурных формул привода. Они построены следующим образом. На равном расстоянии друг от друга проводят вертикальные линии, число которых должно быть на единицу больше, чем число групповых передач. Также проводят ряд горизонтальных параллельных прямых с интервалом, равным 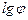(число горизонтальных прямых равно числу 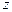ступеней частоты вращения шпинделя). На середине первой слева вертикальной линии наносят точку 0, из которой симметрично в соответствии с числом передач в группах по заданной структурной формуле проводят лучи, соединяющие точки на вертикальных линиях. Расстояние между соседними лучами должны быть равны 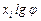, где 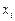- характеристика соответствующей группы.

Оптимальный вариант структурной сетки выбирают из следу­ющих соображений. Выше отмечалось, что независимо от порядка переключений групповых передач диапазон регулирования пос­ледней переборной группы является наибольшим. Поэтому следует определить диапазоны регулирования последних переборных групп для всех вариантов структурных сеток (при выбранном значении 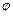) и исключить из дальнейшего рассмотрения варианты, не удовлетворяющие условию

.

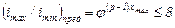Для варианта, показанного на рис. 4, б, 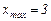, а для варианта, показанного на рис. 4, в, 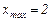. Вариант, при­веденный на рис. 4, б, подходит для всех значений 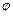, так как 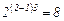; вариант на рис. 4, в удовлетворяет всем значе­ниям 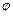за исключением 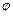= 1,78 и 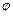= 2, поскольку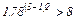 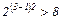. На рис. 4, г, д показаны построенные для обоих вариантов структурных сеток графики частоты вращения при = 1,26, 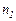= 160 мин^-1, 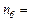500 мин^-1 и 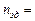1000 об/мин.

Графики частоты вращения строят в следующей последовательности: на равном расстоянии друг от друга проводят вертикальные линии, число которых равно числу валов коробки; на
равном расстоянии друг от друга с интервалами 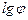проводят
горизонтальные линии, которым присваивают (снизу вверх) порядковые номера частот вращения, начиная с 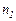. Луч, проведенный
между вертикальными линиями, обозначает передачу между
двумя ралами с передаточным отношением 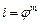, где т — число
интервалов 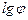, перекрытых лучом. При горизонтальном положении луча 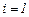, при луче, направленном вверх, 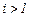, а направленным вниз .

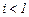Для разбираемого примера ( 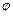= 1,26) с учетом особенностей
отдельных передач и значений предельных передаточных отношени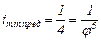й и 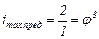(для каждого варианта) сначала цепь передач для снижения частоты вращения от 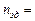1000 об/мин до 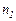= 160 мин^-1. Наиболее целесообразно при этом так разбить общее передаточное отношение цепи, чтобы сохранить более высокими частоты вращения промежуточных валов. В этом случае размеры коробки уменьшаются. Даль­нейшее построение ведем, используя принятые варианты струк­турных сеток. Построенный график частоты вращения позволяет определить передаточные отношения всех передач коробки.

По найденным передаточным отношениям определяют числа зубьев зубчатых колес. Следует иметь в виду, что в станкостроении межосевые расстояния, суммы чисел зубьев сопряженных колес, числа зубьев червячных колес и модули нормализованы. При постоянном расстоянии между осями ведущего и ведомого валов и одинаковом модуле колес группы передач сумма чисел зубьев каждой пары зубчатых колес является постоянной величиной, т.е. .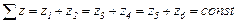

Передаточные отношения пар зубчатых колес, находящихся в зацеплении, 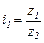; ; 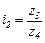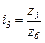и т. д. Из уравнени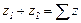й

и 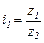следует, что 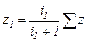и 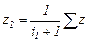. По этим формулам находят числа зубьев колес группы по заданной 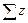. Передаточные отношения 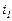, 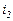и т.д. определяют по графику частоты вращения.