Валентная зона

Электроны в зоне проводимости и дырки в валентной зоне определяют электропроводность полупроводников.

Температурная зависимость концентрации электронов в зоне проводимости, а следовательно, и концентрации образовавшихся при этом дырок определяется соотношением

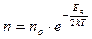. (5)

Тогда проводимость собственных полупроводников изменяется по закону

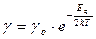. (6)

Увеличение проводимости полупроводников с ростом температуры - главное отличие полупроводников от металлов. С точки зрения зонной теории это обстоятельство объясняется довольно просто: с повышением температуры растет число электронов, которые из-за теплового возбуждения переходят в зону проводимости. Поэтому удельная проводимость собственных полупроводников резко возрастает с ростом температуры, а электрическое сопротивление – резко уменьшается.

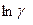
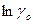
рис.4

Если представить зависимость 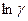как функцию 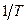, то для собственных полупроводников она представляет прямую (рис.4), по наклону которой можно определить ширину запрещенной зоны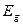 , экстраполируя данную зависимость в область малых значений 1/T.

Зависимость сопротивления полупроводников от температуры описывается следующим выражением:

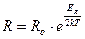, (7)

где 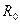- некоторая константа, определяемая из графика путем экстраполяции 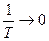(см. пунктирную линию на рис.4).

Прологарифмировав выражение (7), получим:

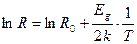. (8)

Формула (8) представляет уравнение прямой в координатах 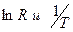. Построив график зависимости сопротивления полупроводника от температуры в координатах 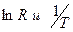, получим прямую линию, как показано на рис.5.

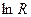
β

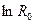
рис.5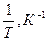

Продолжение прямой до пересечения с осью ординат 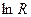определяет значение 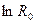. Тангенс угла наклона прямой к оси абсцисс определяет величину постоянной :

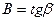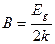. (9)

Данное выражение позволяет определить значение ширины запрещенной зоны:

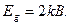(10)