ПРЕДСКАЗАНИЕ И ОЦЕНИВАНИЕ

Тема 8

Задача оценивания Y по X (или X по Υ)

Если задана конкретная оценка для характеристики (переменной) X, то какую информацию можно получить относительно его оценки по характеристике (переменной) Y? Вот некоторые примеры задачи оценивания (когда X предшествует Y, мы предсказываем Y по X, если нам известна связь X и Υ, основанная на предыдущей выборке):

1. Как и насколько хорошо мы можем предсказывать отметки по английскому языку в колледже, зная οтметки в школе? (Школьные отметки предшествуют отметкам в колледже, поэтому мы можем предсказывать последние).

2. Насколько правильно можем мы определить оценки IQ Стенфорда – Бине по оценкам IQ Калифорнийского теста интеллектуальной зрелости? (Никакой обязательной последовательности этих тестов не предполагается, поэтому оценивание необходимо лишь для определения того, насколько близко расположены эквивалентные значения z каждого экзаменующегося по двум тестам).

3. Насколько правильно можем мы предсказывать заработок в 35 лет по рангу в выпускном классе школы?

4. Насколько хорошо мы можем оценивать успеваемость по интеллекту?

Чтобы вывести способ оценивания объекта по одной переменной (мы будем обозначать ее Y) на основе другой переменной (X), мы должны знать, как связаны между собой X и Y. Переменная, которую мы хотим оценить, называется зависимой переменной (откликом) (Y), а переменная, используемая для ее оценки, – независимой переменной (фактором) (X). Например, нам захотелось предсказать успеваемость по математике в девятом классе (зависимая переменная Υ) по результатам группового интеллектуального теста, проведенного в конце восьмого класса (независимая переменная X). Результатами измерения Υ могут быть отметки за контрольную по математике для девятого класса, включающую 50 вопросов. Сначала мы должны собрать данные для некоторого количества учащихся n, интеллект которых мы проверяем в восьмом классе, а успеваемость по математике – в девятом. Далее выводим уравнение, связывающее X и Y в этой группе; мы хотели бы использовать это уравнение в будущем для учащихся, значения X которых известны, а Y нам хотелось бы оценить.

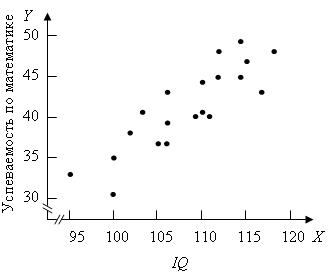
Иллюстративные данные можно табулировать, как, например, это сделано в табл. 8.1, и представить графически, как на рис. 8.1. Из табл. 8.1 видно, что для определения b₁требуется 5 сумм по всем парам (здесь n = 20), причем b₁представляет собой наклон линии регрессии, необходимой для оценки Y (оценки по математике в 9-м классе) по X (IQ в восьмом классе).

Таблица 8.1

Данные для определения линии предсказания

X Независи-мая переменная (IQ в 8-м классе)	Y Зависимая переменная (оценки по математике в 9-м классе)	Вычисления
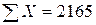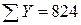
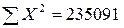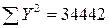
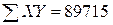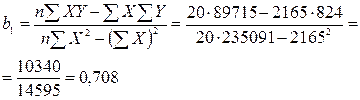
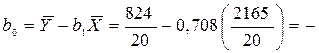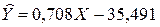		n = 20   35,491   Линия предсказания по методу наименьших квадратов:   .     Другие описательные статистики: ; ; ;

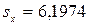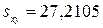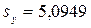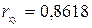
Находим, что b₁ = 0,708 и b₀ = –35,491. Таким образом, уравнение для оценивания Y по X выглядит так: 0,708Х + (–35,491) = 0,708X – 35,491. Прямая, соответствующая этой формуле, изображена на рис. 8.1.

Какой же критерий привел нас к формулам для b₁ и b₀, использованным в табл. 8.1? Это важный вопрос, который заслуживает подробного ответа.

Предположим, мы нашли уравнение для предсказания Y по X, которое обладает удовлетворительными свойствами. Мы имели бы тогда две константы, b₁ и b₀, которые дали бы оцениваемую величину Y. Это означает, что

,

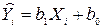предсказанное значение Y для i-гo объекта, обозначенное 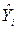, равно произведению b₁ на i-e значение X плюс b₀. Очевидно, 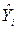не всегда будет равно 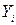, то есть даже при «наилучшем» линейном уравнении предсказания мы, как правило, будем ошибаться в предсказании Y по X.

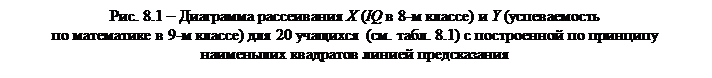
Мы говорим тогда, что

Υ_i = b₁X_i + b₀ + e_i,

где e_i характеризует ошибку оценивания Υ по 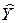для i-гo объекта:

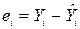. (8.1)

Другое название для e_i – ошибка оценки. Происхождение ошибки оценки в задаче прогнозирования показано на рис. 8.2 для ученика, фактическое значение Υ которого на 4,36 единицы ниже оцениваемого Y, лежащего на линии регрессии.

Как нам следовало бы выбирать b₁ и b₀? Обычно b₁ и b₀ определяются таким образом, чтобы

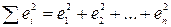
была как можно меньше, то есть чтобы сумма квадратов ошибок оценки была минимальна.

Выбор критерия для подбора b₁ и b₀ является до некоторой степени произвольным.

Критерий наименьших квадратов (то есть минимум суммы квадратов ошибок оценок) не единственно возможный. Хотя на роль критерия для подбора линии регрессии и нет серьезного конкурента, тем не менее существует и другой критерий. Он состоит в том, что b₁ и b₀ выбираются так, чтобы сумма абсолютных величин ошибок, полученных в процессе предсказания, была как можно меньше, то есть минимизируется |e₁| + ... +|е_п|. Этот критерий приводит к «медианной линии регрессии». (Вспомните, что медиана группы данных – это точка, относительно которой сумма абсолютных отклонений минимальна.) Несмотря на простоту вычислений медианной линии регрессии, для нее не существует выводимого теоретического обоснования, какое имеет линия регрессии метода наименьших квадратов.

b₁ задается следующим выражением:

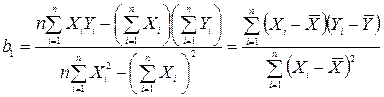, (8.2)

b₀ задается уравнением:

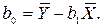(8.3)

Предположим, что мы осуществляем поиск «наилучшего» уравнения для оценивания Y по X, используя прямую, наиболее хорошо подобранную (в смысле принципа наименьших квадратов) по точкам диаграммы рассеивания, и что у нас есть оценки X и Y для 20 учащихся, например, из табл. 8.1.

На данном этапе ничего нельзя сказать относительно того, будут ли зависимая и независимая переменные нормально распределенными или распределенными каким-нибудь другим образом. Чтобы вывести коэффициенты регрессии b₀ и b₁ методом наименьших квадратов, не требовалось никакого представления о форме кривых распределений X и Y. Уравнения (8.2) и (8.3) для b₀ и b₁ дают прямую линию, которая минимизирует сумму квадратов остатков независимо от характера диаграммы рассеивания X и Y.

Если мы делаем некоторые правдоподобные предположения относительно распределений большого числа значений X и Y, то, вероятно, мы должны быть вознаграждены возможностью более тщательного исследования предсказания. Действительно, наше исследование оказывается очень результативным, если мы предполагаем, что X и Y имеют двумерное нормальное распределение (см. § 6.7). Тогда можно полагать, что рассматриваемые n пар значений X и Y образуют случайную выборку из очень большой совокупности X и Y с двумерным нормальным распределением.

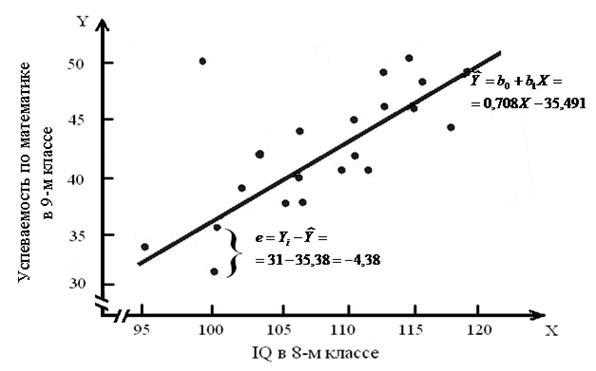
Рис. 8.2 – Пример ошибки оценки для ученика,
имеющего оценку 100 по Х и 31 по Y

Теперь важны следующие свойства двумерного нормального распределения:

1. Выборочные средние Y для каждого значения X лежат на прямой.

2. Для любого значения X соответствующие значения Y нормально распределены.

3. Для любого значения X соответствующие значения Y имеют дисперсию 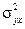, одинаковую для всех X.

Если бы мы могли быть уверенными в том, что n пар значений X и Y исходят из двумерного нормального распределения, то свойство 1 из вышеприведенных говорило бы о том, что использование прямой для прогнозирования Y по X разумно и никакая кривая не может дать лучших результатов. Свойства 2 и 3 можно было бы объединить в очень полезную методику, которая вносит значительный вклад в предсказание Y по X и проблемы оценивания. Эта методика будет рассматриваться далее.