Регистрация частицы
В квантовой механике частица при распространении в пространстве является волной де Бройля с длиной волны
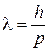 ,
,
где h – постоянная Планка; p – модуль импульса. Состояние частицы описывает комплексная волновая функция
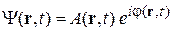 ,
,
где 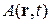 – амплитуда;
– амплитуда; 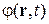 – фаза волны. Состояние изменяется с течением времени обратимо согласно уравнению Шредингера
– фаза волны. Состояние изменяется с течением времени обратимо согласно уравнению Шредингера
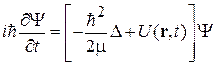 ,
,
где 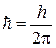 ;
; 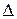 – оператор Лапласа; μ – масса частицы;
– оператор Лапласа; μ – масса частицы; 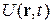 – потенциальная энергия частицы. Например, при равномерном движении частицы с энергией
– потенциальная энергия частицы. Например, при равномерном движении частицы с энергией 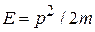 и импульсом p волновая функция
и импульсом p волновая функция
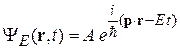
Плотность вероятности обнаружения частицы, т. е. вероятность ее обнаружения в единичном интервале координат, определяется квадратом модуля волновой функции
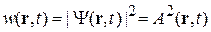 .
.
При каждом измерении положения частицы в состоянии 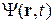 она обнаруживается лишь в одном из возможных мест. Вероятность ее регистрации во всех остальных точках обращается скачком в нуль. Такой одномоментный необратимый процесс преобразования волны в локализованный объект называется редукцией или коллапсом волновой функции, и он не описывается уравнением Шредингера. При повторных регистрациях того же состояния частица обнаруживается в других местах согласно распределению вероятности по координатам
она обнаруживается лишь в одном из возможных мест. Вероятность ее регистрации во всех остальных точках обращается скачком в нуль. Такой одномоментный необратимый процесс преобразования волны в локализованный объект называется редукцией или коллапсом волновой функции, и он не описывается уравнением Шредингера. При повторных регистрациях того же состояния частица обнаруживается в других местах согласно распределению вероятности по координатам 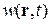 .
.
Эти выводы теории проверил экспериментально A. Tonomura в 1989 г., используя опыт Юнга, показанный на рис. 1. В оптике опыт Юнга демонстрирует волновую природу света. На экран K с двумя щелями направляется волна от источника S. Волна дифрагирует на двух щелях, прошедшие волны накладываются друг на друга и интерферируют, результат регистрируется фотопластинкой M, где возникает интерференционная картина A распределения света, показанная на рис. 1.
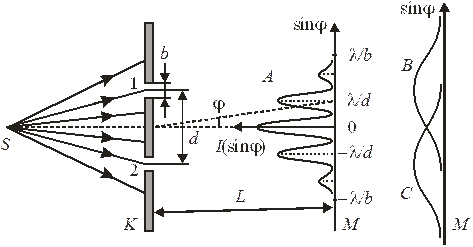
Рис. 1. Опыт Юнга. Распределение частиц на экране M,
прошедших через щели экрана K: А – открыты обе щели;
B – открыта щель 1; C – открыта щель 2
В опыте Tonomura источник S испускал монохроматические электроны с длиной волны де Бройля λ. Размеры щелей в опыте Юнга сравнимы с величиной λ. Результаты многократных повторений опыта с одиночными электронами, которые регистрировались на фотопластинке M в виде точек, показаны на рис. 2. Время экспозиции последовательно увеличивалось при переходе от рис. 2,а к 2,b, 2,c и 2,d и росло число частиц, зарегистрированных в отдельных случайных точках. Постепенно распределение точек регистрации принимало вид интерференционных полос на рис. 2,d. Эксперимент Тономура подтвердил волновую природу электрона при распространении его в пространстве и прохождении через щели. При регистрации электрона фотопластинкой происходит редукция волновой функции, и электрон обнаруживается в виде локализованного объекта.

Рис. 2. Последовательное увеличение числа регистраций
электронов на фотопластинке
Редукция возникает из-за необратимого взаимодействия волны де Бройля с хаотическим окружением в виде зерен фотоэмульсии. Неупругие соударения микрочастицы с хаотической средой вызывают декогеренцию, сбивают фазу волны де Бройля 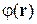 и увеличивают неопределенность импульса частицы, связанного с градиентом фазы волновой функции:
и увеличивают неопределенность импульса частицы, связанного с градиентом фазы волновой функции:
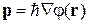 .
.
Согласно соотношению неопределенностей Гейзенберга между координатой и импульсом
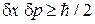 ,
,
с ростом неопределенности импульса уменьшается неопределенность координаты. Состояние частицы преобразуется в локализованный волновой пакет
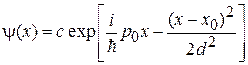
шириной 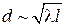 , где λ – длина волны де Бройля; l – длина свободного пробега частицы. Центр пакета находится в точке
, где λ – длина волны де Бройля; l – длина свободного пробега частицы. Центр пакета находится в точке 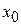 . Плотность вероятности
. Плотность вероятности
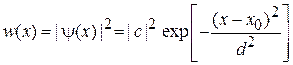
уменьшается по экспоненте при удалении от центра пакета. В результате энергия частицы локализуется, передается зерну фотоэмульсии и вызывает в нем химическую реакцию. После проявления фотопластинки прореагировавшее зерно становится оптически прозрачным. При многократном повторении измерения проявляется статистическая закономерность 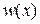 в распределении прореагировавших зерен фотоэмульсии, показанном на рис. 2,d.
в распределении прореагировавших зерен фотоэмульсии, показанном на рис. 2,d.
Дата добавления: 2015-09-21; просмотров: 1165;
