Постоянный электрический ток. Классическая теория электропроводности металлов.

Направленное движение электрических зарядов под действием сил электрического поля назы­вают электрическим током.

Ток может идти в твердых телах, жидко­стях и газах. Если среда является проводником с большим количеством свободных электронов, то течение электрического тока осуществляется за счет дрейфа этих электронов.

Дрейф электронов в проводниках, не свя­занный с перемещением вещества, называют током проводимости. Упорядоченное перемещение электрических зарядов, связанное с перемещением в пространстве за­ряженного тела, называют конвекционным током.За направление тока принят дрейф положительных зарядов. Количественной характеристикой электрического тока являются си­ла тока I и плотность тока j.

Сила тока – скалярная величина, равная отношению количества электричества dq, которое за время dt переносится через данное сече­ние проводника, ко времени dt: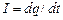

Постоянным током называют электрический ток, сила и направле­ние которого с течением времени не изменяются:

Единица силы электрического тока – ампер (А).

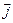Плотность тока – векторная физическая величина, модуль кото­рой равен отношению силы тока I к площади поперечного сечения проводника S: . Вектор направлен вдоль направления тока.

Для металлов, где ток создается движущимися электронами, плотность тока вычисляется по формуле: j = ne 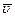, где e – заряд электрона, n – концентрация электронов, 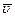– средняя скорость направленного движения электронов.

Для того чтобы в проводнике все время шел ток, необходимо под­держивать в нем постоянное электрическое поле. Возьмем металличе­ский проводник длиной l. Пусть Е – напряженность электрического по­ля внутри проводника, а j₁ – j₂=U – постоянная разность потенциалов на концах проводника. Тогда: .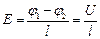

За­кон Ома для участка цепи: сила тока в проводнике пропорциональна напряжению на его концах и обратно пропорциональна сопротивлению проводника: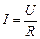

Единица сопротивления – ом (Ом).

Электрическое сопротивление обусловлено тем, что свободные электро­ны при дрейфе взаимодействуют с положительными ионами кристалли­ческой решетки металла. Для однородно­го цилиндрического проводника длиной l и площадью поперечного сече­ния S сопротивление определяется по формуле: R= 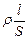, где r– удельное сопротивление проводника. Единица удельного сопротивления – ом-метр (Ом×м).

Величина , обратная удельному сопротивлению, называется удельной электрической проводимостью проводника.

Закон Ома можно представить в дифференциальной форме:

или 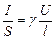. Тогда: j = gE.

Направления векторов j и Е совпадают, так как носители заряда в каждой точке движутся в направлении вектора Е. Следовательно, этот закон можно переписать в виде: .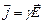

Это закон Ома в дифференциальной форме.

Это закон Ома для полной цепи: 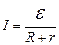, где –ЭДС источника, r–его внутреннее сопротивление. ЭДС источника тока численно равен работе, которую совершают сторонние силы при перемещении еди­ничного положительного электрического заряда вдоль всей цепи.

Количество теплоты, выделяемое в цепи, определяется законом Джоуля - Ленца: 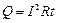. Закон Джоуля–Ленцав дифференциальной форме: 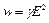, где w–количество теплоты, выделяющееся за единицу времени в единице объема.

В классической электронной теории электроны проводимости рас­сматриваются как электронный газ, подобный идеальному одноатомному газу. Предполагается, что движение электронов подчиняется законам классической механики Ньютона. Взаимодействием электронов между собой пренебрегают и считают, что они взаимодействуют только с положительными ионами решетки. По этой теории электронный газ должен подчиняться всем законам идеаль­ного газа. Согласно закону равномерного распределения энергии по сте­пеням свободы, на один электрон приходится средняя кинетическая энер­гия теплового движения , где k – постоянная Больцмана. При тепловом движении электроны испытывают соударения. Путь, проходимый электронами между двумя последовательными соударениями, называют длиной свободного пробега (l).

Предполагается, что при каждом соударении электрон полностью передает свою энергию ионам решетки (т.е. столкновения неупругие) и начальная скорость последую­щего движения электрона равна нулю. Если по проводнику течет постоянный ток, то внутри проводника существует электрическое поле напряженностью Е. На каждый электрон со стороны электрического поля действует сила F = еЕ. Под действием этой силы электрон приобретает ускорение а, которое можно определить из равенства т_еa=еЕ, откуда

Если t – среднее время между двумя последовательными соуда­рениями, то к концу свободного пробега электрон приобретает скорость . Средняя скорость упорядоченного движения электронов 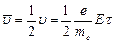(1)

(начальная скорость полагается равной нулю, поэтому движение считает­ся равноускоренным).

Среднее время между двумя последовательными соударениями можно определить, если знать длину свободного пробега и среднюю ско­рость теплового движения ( ): 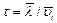. Подставив tв формулу (1), получим (2).

Мы знаем, что плотность тока можно определить из соотношения
j = ne 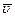. Подставив сюда (2), получим (3), где 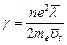(4) – удельная проводимость материала.

Из полученного выражения (3) следует: плот­ность тока пропорциональна напряженности электрического поля, что находится в соответствии с законом Ома в дифференциальной форме.

Анализируя выражение (4), видим, что электропроводимость пропорциональна концентрации п электронов проводимости и средней длине свободного пробега, т.е. чем больше l, тем меньшую помеху для упорядоченного движения электронов представляют соударения. Электропроводимость обратно пропорциональна средней тепловой скорости ( 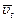). Тепловая скорость при повышении температуры возрастает пропорционально 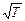, что при­водит к уменьшению электропроводимости и увеличению удельного со­противления проводников.

На основании классической теории проводимости ме­таллов можно объяснить закон Джоуля–Ленца. Упорядоченное движение электронов происходит под действием сил поля. Так как в момент соударения с положи­тельными ионами кристаллической решетки электроны полностью передают ей свою кинетическую энергию, то к концу свободного пробега ско­рость электрона u =eEt /m_e, акинетическая энергия .

Мощность, выделяемая единицей объема металла (плотность мощ­ности), равна произведению энергии одного электрона на число соударе­ний в секунду 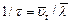и на концентрацию и электронов: .

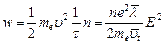Учитывая, что 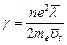, имеем 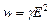. Имеем соответствие с законом Джоуля-Ленца в дифф. форме.

Таким образом, классическая теория электропроводности смогла объяснить законы Ома и Джоуля-Ленца, а также характер зависимости сопротивления от температуры.

Противоречия классической теории:

1) С»3R, хотя по теории должно быть 3R+1,5R (дополнительный вклад теплоемкости электронов).

2) Так как , то r ~ u ~ 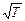, а на практике: 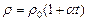, то есть r ~Т.

3) не объясняет природу сверхпроводимости (отсутствии сопротивления при низких температурах)

4) Величина средней длины светового пробега электрона, получаемая по формулам, на два порядка превышает период кристаллической решетки металла

Данные затруднения были преодолены с помощью квантовой теории.